HDU100题简要题解(2040~2049)
HDU2040 亲和数
Problem Description
古希腊数学家毕达哥拉斯在自然数研究中发现,220的所有真约数(即不是自身的约数)之和为:
1+2+4+5+10+11+20+22+44+55+110=284。
而284的所有真约数为1、2、4、71、 142,加起来恰好为220。人们对这样的数感到很惊奇,并称之为亲和数。一般地讲,如果两个数中任何一个数都是另一个数的真约数之和,则这两个数就是亲和数。
你的任务就编写一个程序,判断给定的两个数是否是亲和数
Input
输入数据第一行包含一个数M,接下有M行,每行一个实例,包含两个整数A,B; 其中 0 <= A,B <= 600000 ;
Output
对于每个测试实例,如果A和B是亲和数的话输出YES,否则输出NO。
Sample Input
2
220 284
100 200
Sample Output
YES
NO
求每个数的真约数和与另一个数进行比较就好了
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int m;
int cal(int x) {
int cnt = 0;
for (int i = 1; i < x; i++)
if (x % i == 0) cnt += i;
return cnt;
}
int main() {
while (scanf("%d", &m) != EOF) {
for (int i = 1; i <= m; i++) {
int a, b;
scanf("%d%d", &a, &b);
int num1 = cal(a);
int num2 = cal(b);
if (a == num2 && b == num1) printf("YES\n");
else printf("NO\n");
}
}
return 0;
}
HDU2041 超级楼梯
Problem Description
有一楼梯共M级,刚开始时你在第一级,若每次只能跨上一级或二级,要走上第M级,共有多少种走法?
Input
输入数据首先包含一个整数N,表示测试实例的个数,然后是N行数据,每行包含一个整数M(1<=M<=40),表示楼梯的级数。
Output
对于每个测试实例,请输出不同走法的数量
Sample Input
2
2
3
Sample Output
1
2
十分经典的题目,到达第n个台阶可以从第n-1级台阶跨一级上来,也可以从第n-2级台阶跨两级上来
所以我们很容易得到递推公式a[n] = a[n - 1] + a[n - 2]
注意初始化a[2] = 1; a[3] = 2
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m, dp[41];
int main() {
while (scanf("%d", &n) != EOF) {
dp[2] = 1;
dp[3] = 2;
for (int i = 1; i <= n; i++) {
scanf("%d", &m);
for (int i = 4; i <= m; i++) dp[i] = dp[i - 1] + dp[i - 2];
printf("%d\n", dp[m]);
}
}
return 0;
}
HDU2042 不容易系列之二
Problem Description
你活的不容易,我活的不容易,他活的也不容易。不过,如果你看了下面的故事,就会知道,有位老汉比你还不容易。
重庆市郊黄泥板村的徐老汉(大号徐东海,简称XDH)这两年辛辛苦苦养了不少羊,到了今年夏天,由于众所周知的高温干旱,实在没办法解决牲畜的饮水问题,就决定把这些羊都赶到集市去卖。从黄泥板村到交易地点要经过N个收费站,按说这收费站和徐老汉没什么关系,但是事实却令徐老汉欲哭无泪:
中间一堆废话......这里略过......
由于徐老汉没钱,收费员就将他的羊拿走一半,看到老汉泪水涟涟,犹豫了一下,又还给老汉一只。巧合的是,后面每过一个收费站,都是拿走当时羊的一半,然后退还一只,等到老汉到达市场,就只剩下3只羊了。
你,当代有良知的青年,能帮忙算一下老汉最初有多少只羊吗?
Input
输入数据第一行是一个整数N,下面由N行组成,每行包含一个整数a(0<a<=30),表示收费站的数量。
Output
对于每个测试实例,请输出最初的羊的数量,每个测试实例的输出占一行。
Sample Input
2
1
2
Sample Output
4
6
和之前吃蟠桃一个样子的,只是蟠桃是每次吃掉一半多一个,现在是羊每次拿走一半少一个
稍微做一下改动即可
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m, sum = 1;
int main() {
while (scanf("%d", &n) != EOF) {
for (int i = 1; i <= n; i++) {
scanf("%d", &m);
sum = 3;
while (m--) sum = 2 * (sum - 1);
printf("%d\n", sum);
}
}
return 0;
}
HDU2043 密码
Problem Description
网上流传一句话:"常在网上飘啊,哪能不挨刀啊~"。其实要想能安安心心地上网其实也不难,学点安全知识就可以。
首先,我们就要设置一个安全的密码。那什么样的密码才叫安全的呢?一般来说一个比较安全的密码至少应该满足下面两个条件:
(1).密码长度大于等于8,且不要超过16。
(2).密码中的字符应该来自下面“字符类别”中四组中的至少三组。
这四个字符类别分别为:
1.大写字母:A,B,C...Z;
2.小写字母:a,b,c...z;
3.数字:0,1,2...9;
4.特殊符号:~,!,@,#,$,%,^;
给你一个密码,你的任务就是判断它是不是一个安全的密码。
Input
输入数据第一行包含一个数M,接下有M行,每行一个密码(长度最大可能为50),密码仅包括上面的四类字符。
Output
对于每个测试实例,判断这个密码是不是一个安全的密码,是的话输出YES,否则输出NO。
Sample Input
3
a1b2c3d4
Linle@ACM
~@^@!%
Sample Output
NO
YES
NO
做这题的时候好像还在JNUCTF期间,满脑子弱口令,边做还边想这给的样例跑字典跑不出来啊...
咳咳回归正题,就是判断每一个制胡窜是不是都包含四种字符中的三种,具体判断见代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int m;
char a[51];
int main() {
while (scanf("%d", &m) != EOF) {
getchar();
for (int i = 1; i <= m; i++) {
int num1, num2, num3, num4;
num1 = num2 = num3 = num4 = 0;
gets(a);
int len = strlen(a);
if (len < 8 || len > 16) {
printf("NO\n");
continue;
}
for (int i = 0; i < len; i++) {
if ('a' <= a[i] && 'z' >= a[i]) num1 = 1;
if ('A' <= a[i] && 'Z' >= a[i]) num2 = 1;
if ('0' <= a[i] && '9' >= a[i]) num3 = 1;
if (a[i] == '~' || a[i] == '!' || a[i] == '@' || a[i] == '#' || a[i] == '$' || a[i] == '%' || a[i] == '^') num4 = 1;
}
int num = num1 + num2 + num3 + num4;
if (num >= 3) printf("YES\n");
else printf("NO\n");
}
}
return 0;
}
HDU2044 一只小蜜蜂...
Problem Description
有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房,不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中,蜂房的结构如下所示。
Input
输入数据的第一行是一个整数N,表示测试实例的个数,然后是N 行数据,每行包含两个整数a和b(0<a<b<50)。
Output
对于每个测试实例,请输出蜜蜂从蜂房a爬到蜂房b的可能路线数,每个实例的输出占一行。
Sample Input
2
1 2
3 6
Sample Output
1
3
经典题目了,10月左右安徽大学acm新生赛好像还出了一道这题的变形,这里整一个高精版的:洛谷P2437蜜蜂路线
同样也是一个斐波那契数列,第m个蜂房可以通过第m-1和第m-2个蜂房到达,剩下的就和楼梯那题一个样了
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
long long n, dp[1001];
int main() {
while (scanf("%lld", &n) != EOF) {
dp[1] = 1;
dp[2] = 2;
for (int i = 1; i <= n; i++) {
long long a, b;
scanf("%lld%lld", &a, &b);
for (int i = 3; i <= b - a; i++) dp[i] = dp[i - 1] + dp[i - 2];
printf("%lld\n", dp[b - a]);
}
}
return 0;
}
HDU2045 不容易系列之(3)—— LELE的RPG难题
Problem Description
人称“AC女之杀手”的超级偶像LELE最近忽然玩起了深沉,这可急坏了众多“Cole”(LELE的粉丝,即"可乐"),经过多方打探,某资深Cole终于知道了原因,原来,LELE最近研究起了著名的RPG难题:
有排成一行的n个方格,用红(Red)、粉(Pink)、绿(Green)三色涂每个格子,每格涂一色,要求任何相邻的方格不能同色,且首尾两格也不同色.求全部的满足要求的涂法.
以上就是著名的RPG难题.
如果你是Cole,我想你一定会想尽办法帮助LELE解决这个问题的;如果不是,看在众多漂亮的痛不欲生的Cole女的面子上,你也不会袖手旁观吧?
Input
输入数据包含多个测试实例,每个测试实例占一行,由一个整数N组成,(0<n<=50)。
Output
对于每个测试实例,请输出全部的满足要求的涂法,每个实例的输出占一行。
Sample Input
1
2
Sample Output
3
6
这题当时想了挺久的,看了题解又想了很久才懂,这里详细说一下吧
核心代码为:f[i] = f[i - 1] + f[i - 2] * 2;
但是为啥子嘞?我们以5个格子的情况举例
假设五个格子,三个颜色:红黄蓝,第一个格子假设涂红色
先看第一种情况(5 = 4 + 1):
-先涂好四个格子,则第四个格子和第一个格子颜色一定不一样,那么第五个格子有且只有一种取法
-在此情况下的方案数为f[4]
再看第二种情况(5 = 3 + 2):
-先涂好三个格子,再涂后两个,则此时第四个格子是不会受到第一个格子的颜色的约束的,由于第一种情况已经计算了第四个格子为黄蓝的情况,我们这里只需考虑红色即可,此时第五个格子便可取黄蓝
-所以在这个情况下的方案数为f[3] * 2
总的来说,第五个格子的方案数即为f[4] + f[3] * 2
其余同理
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
long long n, f[1001];
int main() {
while (scanf("%lld", &n) != EOF) {
f[0] = 0;
f[1] = 3;
f[2] = 6;
f[3] = 6;
for (int i = 4; i <= n; i++)
f[i] = f[i - 1] + f[i - 2] * 2;
printf("%lld\n", f[n]);
}
return 0;
}
HDU2046 骨牌铺方格
Problem Description
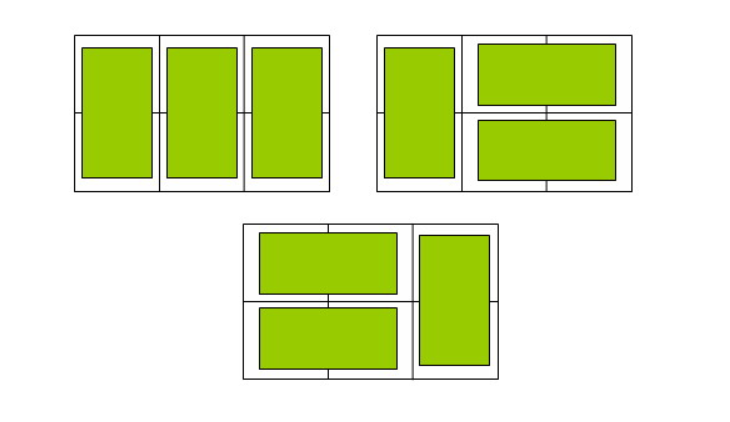
在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.
例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图:
Input
输入数据由多行组成,每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。
Output
对于每个测试实例,请输出铺放方案的总数,每个实例的输出占一行。
Sample Input
1
3
2
Sample Output
1
3
2
又是递推...好多递推题啊...
递推式还是那个递推式,可以解释为在f[n-1]的基础上竖着加一个长方块以及在f[n-2]的基础上横着放俩长方块
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
long long n, dp[51];
int main() {
while (scanf("%lld", &n) != EOF) {
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++)
dp[i] = dp[i - 1] + dp[i - 2];
printf("%lld\n", dp[n]);
}
return 0;
}
HDU2047 阿牛的EOF牛肉串
Problem Description
今年的ACM暑期集训队一共有18人,分为6支队伍。其中有一个叫做EOF的队伍,由04级的阿牛、XC以及05级的COY组成。在共同的集训生活中,大家建立了深厚的友谊,阿牛准备做点什么来纪念这段激情燃烧的岁月,想了一想,阿牛从家里拿来了一块上等的牛肉干,准备在上面刻下一个长度为n的只由"E" "O" "F"三种字符组成的字符串(可以只有其中一种或两种字符,但绝对不能有其他字符),阿牛同时禁止在串中出现O相邻的情况,他认为,"OO"看起来就像发怒的眼睛,效果不好。
你,NEW ACMer,EOF的崇拜者,能帮阿牛算一下一共有多少种满足要求的不同的字符串吗?
PS: 阿牛还有一个小秘密,就是准备把这个刻有 EOF的牛肉干,作为神秘礼物献给杭电五十周年校庆,可以想象,当校长接过这块牛肉干的时候该有多高兴!这里,请允许我代表杭电的ACMer向阿牛表示感谢!
再次感谢!
Input
输入数据包含多个测试实例,每个测试实例占一行,由一个整数n组成,(0<n<40)。
Output
对于每个测试实例,请输出全部的满足要求的涂法,每个实例的输出占一行。
Sample Input
1
2
Sample Output
3
8
和RPG那题大同小异,也是两种情况
第一种:n-1不是O,方案数就是f[n-1] * 2
第二种:n-1是O,方案数就是f[n-2] * 2
得到递推式f[n] = f[n-2] * 2 + f[n-1] * 2
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
long long a[51];
int main() {
while (scanf("%d", &n) != EOF) {
a[1] = 3;
a[2] = 8;
for (int i = 3; i <= n; i++)
a[i] = 2 * a[i - 1] + 2 * a[i - 2];
printf("%lld\n", a[n]);
}
return 0;
}
HDU2048 神、上帝以及老天爷
Problem Description
HDU 2006'10 ACM contest的颁奖晚会隆重开始了!
为了活跃气氛,组织者举行了一个别开生面、奖品丰厚的抽奖活动,这个活动的具体要求是这样的:
首先,所有参加晚会的人员都将一张写有自己名字的字条放入抽奖箱中;
然后,待所有字条加入完毕,每人从箱中取一个字条;
最后,如果取得的字条上写的就是自己的名字,那么“恭喜你,中奖了!”
大家可以想象一下当时的气氛之热烈,毕竟中奖者的奖品是大家梦寐以求的Twins签名照呀!不过,正如所有试图设计的喜剧往往以悲剧结尾,这次抽奖活动最后竟然没有一个人中奖!
我的神、上帝以及老天爷呀,怎么会这样呢?
不过,先不要激动,现在问题来了,你能计算一下发生这种情况的概率吗?
不会算?难道你也想以悲剧结尾?!
Input
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C 行数据,每行包含一个整数n(1<n<=20),表示参加抽奖的人数。
Output
对于每个测试实例,请输出发生这种情况的百分比,每个实例的输出占一行, 结果保留两位小数(四舍五入),具体格式请参照sample output。
Sample Input
1
2
Sample Output
50.00%
高中数学,排列组合
阿巴阿巴阿巴,好像是那个什么错排,错排是啥早忘了,看了一眼题解才想起来
求概率其实就是分子(错排)/分母(n!)。分母很好算,我们接下来考虑一下分子
考虑第n个数,假设把它放在了k的位置上,有n-1种方法,那么对于第k个数字放在哪里,又可以分两种情况讨论:
1、把第k个数放在n的位置上,那么就是剩下的n-2个数的错排问题
2、不把第k个数放在n的位置上,那么就是剩下n-1个数的错排问题
所以分子的递推关系式为:f[n] = (n - 1) * (f[n - 1] + f[n - 2]),注意初始化a[1] = 0; a[2] = 1;
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
double a[21], b[21];
int main() {
while (scanf("%d", &n) != EOF) {
for (int i = 1; i <= n; i++) {
scanf("%d", &m);
a[1] = 0;
a[2] = 1;
b[1] = 1;
b[2] = 2;
for (int i = 3; i <= m; i++) {
a[i] = (i - 1) * (a[i - 1] + a[i - 2]);
b[i] = b[i - 1] * i;
}
printf("%.2lf%%\n", (a[m] / b[m]) * 100);
}
}
return 0;
}
HDU2049 不容易系列之(4)——考新郎
Problem Description
国庆期间,省城HZ刚刚举行了一场盛大的集体婚礼,为了使婚礼进行的丰富一些,司仪临时想出了有一个有意思的节目,叫做"考新郎",具体的操作是这样的:
首先,给每位新娘打扮得几乎一模一样,并盖上大大的红盖头随机坐成一排;
然后,让各位新郎寻找自己的新娘.每人只准找一个,并且不允许多人找一个.
最后,揭开盖头,如果找错了对象就要当众跪搓衣板...
看来做新郎也不是容易的事情...
假设一共有N对新婚夫妇,其中有M个新郎找错了新娘,求发生这种情况一共有多少种可能.
Input
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C行数据,每行包含两个整数N和M(1<M<=N<=20)。
Output
对于每个测试实例,请输出一共有多少种发生这种情况的可能,每个实例的输出占一行。
Sample Input
2
2 2
3 2
Sample Output
1
3
高中排列组合,从n中选出m个,然后乘上错排公式,即C[m][n] * f[n](f[n]为n的错排)
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
int c, n, m;
long long f[21];
long long work(int n, int m) {
long long sum1, sum2;
sum1 = sum2 = 1;
for (int i = n; i >= n - m + 1; i--)
sum1 *= i;
for (int i = 1; i <= m; i++)
sum2 *= i;
return sum1/sum2;
}
int main() {
while (scanf("%d", &c) != EOF) {
for (int i = 1; i <= c; i++) {
scanf("%d%d", &n, &m);
long long ans;
f[1] = 0;
f[2] = 1;
for (int j = 3; j <= m; j++)
f[j] = (j - 1) * (f[j - 1] + f[j - 2]);
ans = work(n, m) * f[m];
printf("%lld\n", ans);
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号