计算图--叶子节点、with torch.no_grad()学习

参考连接1：https://zhuanlan.zhihu.com/p/416083478     更清楚

参考连接2：https://blog.csdn.net/weixin_43178406/article/details/89517008    更全面

1、requires_grad

在pytorch中，tensor有一个requires_grad参数，如果设置为True，则反向传播时，该tensor就会自动求导。tensor的requires_grad的属性默认为False。

1. 若一个节点（叶子变量：自己创建的tensor）requires_grad被设置为True，那么所有依赖它的节点requires_grad都为True（即使其他相依赖的tensor的requires_grad = False）。--待验证（代码具体实现不了）
2. 一个requires_grad为真的tensor可以backward()，而backward()就是根据计算图求梯度

 

a = torch.tensor([1.1], requires_grad=True)
b = a * 2
b

#  tensor([2.2000], grad_fn=<MulBackward0>)

a
#  tensor([1.1000], requires_grad=True)
a.requires_grad
#  True

b.backward()
a.grad

#  tensor([2.])

 

接着继续：

a = torch.tensor([1.1], requires_grad=True)
b = a * 2
b

#  tensor([2.2000], grad_fn=<MulBackward0>)  ---grad_fn 为 mulbackward 表示是做的乘法

b.add_(2)
#  tensor([4.2000], grad_fn=<AddBackward0>) ---grad_fn 为AddBackward0表示是做的加法
b.backward()
a.grad

#  tensor([2.])

#注，需要重新给b赋值运算，否则就会报错--或者在b.backward()中添加保留计算图的操作，具体见下。

 

如果不设置则会出现如下情况：

 

a = torch.tensor([1.1])
b = a * 2
b

#  tensor([2.2000])

a
#  tensor([1.1000])

b.backward()

# RuntimeError  element 0 of tensors does not require grad and does not have a grad_fn

 

x = torch.randn(10, 5, requires_grad = True)
y = torch.randn(10, 5, requires_grad = False)
z = torch.randn(10, 5, requires_grad = False)
w = x + y + z
w.requires_grad

#  True

 

2、with torch.no_grad

a = torch.tensor([1.1], requires_grad=True)
b = a * 2
print(b)
c = b + 3
print(c)
b.backward(retain_graph=True)
#计算图在backward一次之后默认就消失，我们下面还要backward一次，所以需要retain_graph=True保存这个图。
print(a.grad)
c.backward()
print(a.grad)

#  tensor([2.2000], grad_fn=<MulBackward0>)
#  tensor([5.2000], grad_fn=<AddBackward0>)
#  tensor([2.])
#  tensor([4.])   ### 梯度自动累加，没有清零

 添加清零操作

a = torch.tensor([1.1], requires_grad=True)
b = a * 2
c = b + 3
b.backward(retain_graph=True)
print(a.grad)
a.grad.zero_()
b=b*3
b.backward(retain_graph=True)
print(a.grad)
a.grad.zero_()
#tensor分为a.data和a.grad。这两个都是tensor。
#所以也可以a.grad=torch.tensor([0.0])
c.backward()
print(a.grad)

#  tensor([2.])
#  tensor([6.])
#  tensor([2.])

 

3、计算图

• 如图中a、2、3是叶子节点
• b(2.2）是非叶子节点
• Pytorch中不会对非叶子节点保存梯度，故c对b求梯度，结果输出None。
• 当grad_fn为None时，无论requires_grad为True还是False，都为叶子变量，即只要是直接初始化的就为叶子变量。
• 当grad_fn不为None时，requires_grad = False为叶子变量，requires_grad = True为非叶子变量

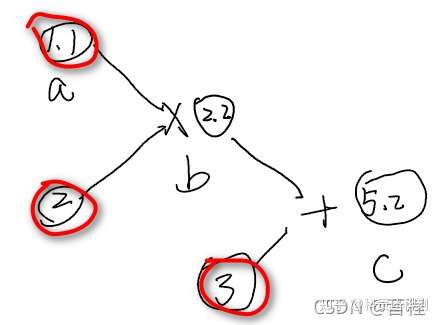
a = torch.tensor([1.1], requires_grad=True)
b = a * 2
c = b + 3
c.backward()
print(a.grad)
print(b.grad)

#  tensor([2.])
#  None

 

 

4、with torch.no_grad

4.1、参数volatile

    如果一个tensor的volatile = True，那么所有依赖他的tensor会全部变成True，反向传播时就不会自动求导了，因此大大节约了显存或者说内存。

1. volatile=True的优先级高于requires_grad，即当volatile = True时，无论requires_grad是Ture还是False，反向传播时都不会自动求导。
2. volatile可以实现一定速度的提升，并节省一半的显存，因为其不需要保存梯度。
3. volatile默认为False，这时反向传播是否自动求导，取决于requires_grad。

4.2、with torch.no_grad

    上文提到volatile已经被废弃，替代其功能的就是with torch.no_grad。作用与volatile相似。

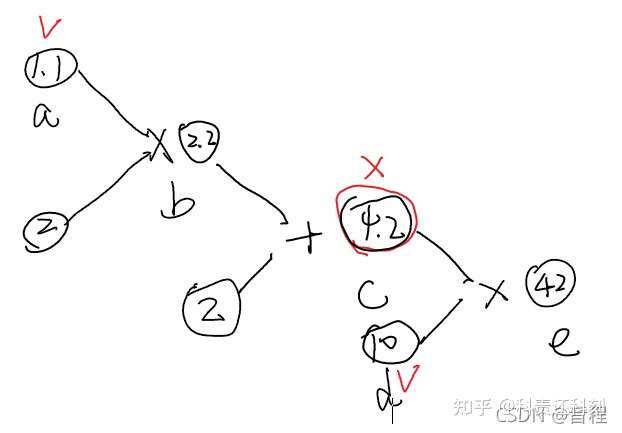
在with torch.no_grad(): 的包裹下，即使一个tensor（命名为x）的requires_grad = True，由x得到的新tensor（命名为w-标量）requires_grad也为False，

且grad_fn也为None,即不会对w求导。

 

a = torch.tensor([1.1], requires_grad=True)
b = a * 2
print("b:",b)
with torch.no_grad():
    c = b + 2
    print('c:',c)
print('c.requires_grad',c.requires_grad)

d = torch.tensor([10.0], requires_grad=True)
e = c * d
print('e.requires_grad:',e.requires_grad)

e.backward()
print('d.grad:',d.grad)
print('a.grad:',a.grad)


#  b: tensor([2.2000], grad_fn=<MulBackward0>)
#  c: tensor([4.2000])
#  c.requires_grad: False     #with torch.no_grad():包裹下
#  e.requires_grad: True
#  d.grad: tensor([4.2000])
#  a.grad: None  #非叶子节点c作为“中间人”，如果其requires_grad=False，那么其前面的所有变量都无法反向传播，自然也就没有梯度，相当于卡住了。

 

 

 

 

x = torch.randn(10, 5, requires_grad = True)
y = torch.randn(10, 5, requires_grad = True)
z = torch.randn(10, 5, requires_grad = True)
with torch.no_grad():
    w = x + y + z
    print(w.requires_grad)
    print(w.grad_fn)
print(w.requires_grad)

#  False
#  None
#  False

 5、关于参数更新

• -= 的说明：可以认为是在原地修改（in-place）。即之前申请的内存地址不变，仅是数据发生了变化，
• -=只有在grad_fn为None且requires_grad = True的时候不适用，其他情况都可以；
• 加上with torch.no_grad（），在计算时，认为param的requires_grad = False，因此可以进行-=，但是-=结束，新的param的requires_grad仍旧为True(即一开始设定的情况)。

with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

 

b=torch.tensor([5.])
id(b),b

#  (140203705353056, tensor([5.]))

a=2
b-=a
id(b),b

#  (140203705353056, tensor([3.]))   #地址没有改变

a=2
b=b-a
id(b),b

#  (140206216604384, tensor([1.]))   #地址改变

a=3
b=-a
b

#  -3 <==>b=(-a)