2020 OO 第一单元总结 表达式求导
title: BUAA-OO 第一单元总结 date: 2020-03-19 20:53:41 tags: OO categories: 学习
OO第一单元通过三次递进式的作业让我们实现表达式求导,在这几次作业中我也有很多收获。下面就回顾一下前三次作业中存在的问题。
在个人看来,表达式求导的难点主要有三部分——对输入的处理、表达式的存储结构以及化简。这三次作业我所采用的表达式存储结构都不相同,不过重构的速度还是比较快的(安慰自己)。
第一次作业
在第一次作业中,我的程序总体架构为提取幂函数为Poly对象,建立Polynomial类解析表达式创建幂函数对象,在主类Derivative中进行部分性能优化工作。
① 程序结构分析
UML类图:
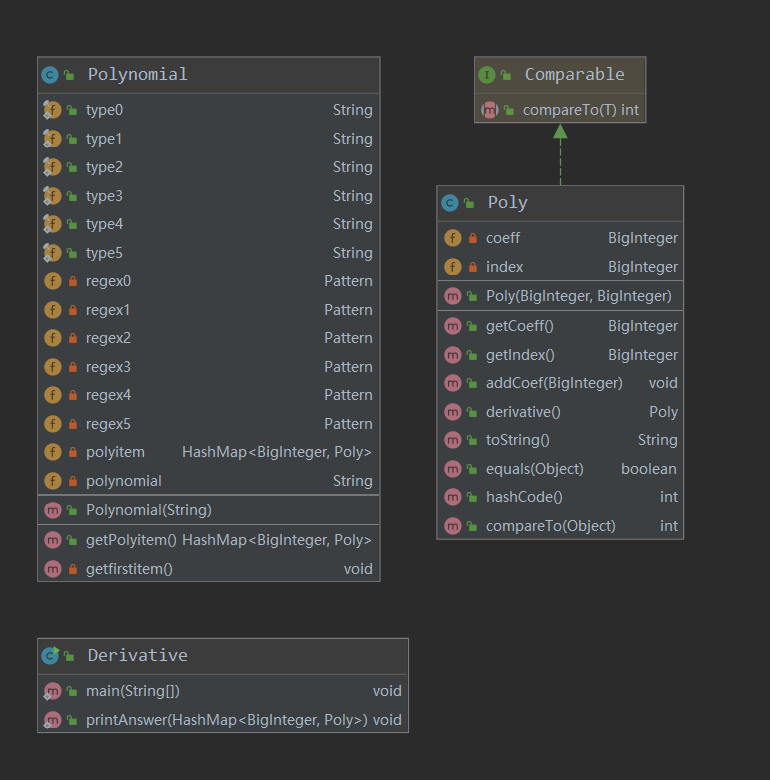

第一次作业的幂函数因子较为简单,代码中仅提炼出Poly对象,并在其内部实现求导方法。
Method复杂度:
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| Derivative.main(String[]) | 1 | 1 | 1 |
| Derivative.printAnswer(HashMap<BigInteger, Poly>) | 4 | 5 | 7 |
| Poly.Poly(BigInteger,BigInteger) | 1 | 1 | 1 |
| Poly.addCoef(BigInteger) | 1 | 1 | 1 |
| Poly.compareTo(Object) | 1 | 1 | 1 |
| Poly.derivative() | 1 | 2 | 2 |
| Poly.equals(Object) | 2 | 2 | 2 |
| Poly.getCoeff() | 1 | 1 | 1 |
| Poly.getIndex() | 1 | 1 | 1 |
| Poly.hashCode() | 1 | 1 | 1 |
| Poly.toString() | 1 | 11 | 12 |
| Polynomial.Polynomial(String) | 1 | 1 | 1 |
| Polynomial.getPolyitem() | 1 | 2 | 2 |
| Polynomial.getfirstitem() | 1 | 9 | 10 |
第一次作业中,化简主要在主类Derivative的printAnswer()方法(将第一个正项优先输出)和Poly类的toString()方法中,printAnswer()涉及对表达式的遍历,基本复杂性高;toString()则包含大量条件语句,多次调用了BigInteger中的方法,循环依赖性高。而表达式解析我采用的是正则+状态机的策略(这个策略三次作业均沿用,感觉还是很舒服的),在getfirstitem()中处理不同类型输入并归一化,代码较为复杂。
② 程序Bug分析
第一次作业在强测、互测中均未出现Bug。
③ 互测采用策略
互测时我采用的策略是“补刀”。我先是用简单的自动测试程序跑了下房间内成员的代码,不过貌似没有出现问题;然而圣杯战争发生了转机——Rider竟然拿下了一血!
于是我一一检查其他成员的代码,发现Berserker的正则存在问题:在正则中匹配的是“[+|-]{0,2}(\\d*.)?x(..[+|-]?\\d+)?”,其中的“.”可匹配任意字符,就会错误解析表达式。
第一次互测时认真读了屋内其他同学的代码,感觉还是很有收获的。之后两次大部分都读不下去,可读性实在是让人肝疼……放到评测姬里自生自灭吧!另外这次互测也让我意识到了高工同学的可怕之处(误),全屋子就这一个Bug,大佬换着花样hack……卷卷更健康。
④ 对象创建模式
在第一次作业中,我并没有应用对象创建模式,表达式解析就顺便new了新因子,Polynomial类的紧耦合比较严重。
第二次作业
第二次作业增加了三角函数因子,这个时候我也偷偷看了一下去年的第三次作业题目,新增加的嵌套对于表达式的化简无疑是不小的挑战。所以在规划第二次作业的总体架构时,我就面临着一个选择——是要建立终将在第三次作业重构的四元组项;还是要采用“表达式-项-因子”三层结构,为第三次作业留好迭代的空间?
经过一番挣扎(其实并没有,因为我还不会写三层结构),我选择了势必带来重构的四元组形式,也就是将表达式的每一项以“coeff*x**powindex*sin(x)**sinindex*cos(x)**cosindex”的形式存储,这样处理方式就和第一次作业基本一致。在基本架构沿用第一次作业的情况下,第二次作业给我最大的挑战反而是三角函数的化简,我的化简类Simplify的行数是最多的。

① 程序结构分析
UML类图:


架构基本沿用第一次作业,UML也差不多,不过这次的简化更复杂一些。
Method复杂度:
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| DeriPrinter.DeriPrinter(HashMap<String, MutiItem>) | 1 | 7 | 7 |
| DeriPrinter.getAnswer(HashMap<String, MutiItem>) | 4 | 5 | 7 |
| DeriPrinter.printAnswer() | 1 | 2 | 2 |
| Item.Item(BigInteger,BigInteger,BigInteger) | 1 | 1 | 1 |
| Item.compareTo(Object) | 3 | 3 | 3 |
| Item.equals(Object) | 2 | 4 | 4 |
| Item.getCosin() | 1 | 1 | 1 |
| Item.getPowin() | 1 | 1 | 1 |
| Item.getSinin() | 1 | 1 | 1 |
| Item.hashCode() | 1 | 1 | 1 |
| Item.toString() | 1 | 5 | 8 |
| MainClass.main(String[]) | 1 | 1 | 1 |
| MutiItem.MutiItem(BigInteger,BigInteger,BigInteger,BigInteger) | 1 | 1 | 1 |
| MutiItem.MutiItem(BigInteger,Item) | 1 | 1 | 1 |
| MutiItem.addCoeff(BigInteger) | 1 | 1 | 1 |
| MutiItem.compareTo(Object) | 1 | 1 | 1 |
| MutiItem.derivate() | 1 | 5 | 5 |
| MutiItem.equals(Object) | 2 | 2 | 2 |
| MutiItem.getCoeff() | 1 | 1 | 1 |
| MutiItem.getCosin() | 1 | 1 | 1 |
| MutiItem.getIdentity() | 1 | 1 | 1 |
| MutiItem.getItem() | 1 | 1 | 1 |
| MutiItem.getPowin() | 1 | 1 | 1 |
| MutiItem.getSinin() | 1 | 1 | 1 |
| MutiItem.hashCode() | 1 | 1 | 1 |
| MutiItem.toString() | 1 | 5 | 5 |
| ParseExp.MutiItemSign() | 2 | 3 | 4 |
| ParseExp.ParseExp(String) | 1 | 5 | 6 |
| ParseExp.WrongFormat(String) | 1 | 1 | 1 |
| ParseExp.getExpression() | 1 | 2 | 2 |
| ParseExp.getFirstitem() | 3 | 13 | 14 |
| Simplify.Simplify(HashMap<String, MutiItem>) | 1 | 2 | 2 |
| Simplify.exitmatch(BigInteger,Item,Item,Item,HashMap<Item, BigInteger>) | 2 | 3 | 4 |
| Simplify.searchcos(HashMap<Item, BigInteger>) | 4 | 6 | 9 |
| Simplify.simplify() | 1 | 3 | 4 |
由于一开始并没有明确的化简思路,在第一遍实现了基本求导功能的代码通过中测之后,我为了实现化简功能,又对代码内类的结构做了很多修改,在这一过程中,尽管我确实用类将表达式中的Item与MulItem做了封装,但我却胡乱修改内部方法,这并不符合面向对象的思想,也导致最后代码可读性极差,也为互测时被发现的Bug埋下了祸根。具体表现到MetricReloaded的分析上,就是ParseExp类的getFirstitem()依然是复杂度重灾区,没有采用工厂模式也使得它与其他类的依赖极为严重,优化输出的内容依然有很高的基本复杂性。
② 程序Bug分析
强测中获得性能分为16.545/20,在处理表达式化简时,我所采用的是暴力搜索的方式,每次搜索到可以合并的项就将其合并,然后进行重新搜索。
这种方法显然只能找到一个极优解,却不能找到最优解,表达式项存储顺序对结果也有很大影响。一种更加可行的方式是采用深度优先搜索,不过当时并没有想出具体的实现方法,只好作罢。
互测时被找出来一个Bug,同时发现Berserker的一个Bug(狂战士日常躺枪)。而我的Bug是HashMap的Key写错,在生成MulItem的Key时,我采用的是将指数拼接为String的方式,在指数较大时,可能会导致不同项被当作同一项存入HashMap中,造成求导错误。
修改也很简单,只需要在生成String的时候给不同指数加个分隔符就好了——
public MutiItem(BigInteger a, BigInteger b, BigInteger c, BigInteger d) {
this.coeff = a;
this.item = new Item(b, c, d);
// before: identity = "" + b + c + d;
identity = "" + b + "." + c + "." + d;
}
可以发现这里我的MutiItem的构造方法是非常混乱的,不过没有发现这么明显的Bug,一方面就是混乱的优化带来的副作用;另一方面也是因为这样的数据出现几率确实很小,同屋里也只有一个同学发现了这个Bug(我后来和hack我的同学交流了下,果然是长时间跑随机自动测试程序才找到的……)
③ 互测采用策略
在这次互测是采用对拍+手动构造样例+Python生成随机数据自动评测的方式。屋内除我只有一个Bug,大家很快找到之后也比较佛系。
互测中阅读了同屋子大佬处理简化的DFS,确实厉害;另外还拜读了另一个房间Alterego的架构,类似Sympy的表达式结构简直叫人拍案叫绝,计算方式优美,让我看到了什么是真正的封装、多态、继承,也有更多信心去面对第三次作业。(不过听说在那个屋Alterego被hack的很惨,悲)
④ 对象创建模式
在第二次作业中,由于使用的是和第一次作业类似的四元组项,我依然没有应用对象创建模式,表达式解析里又new了新因子,紧耦合依然严重。这在第三次作业中有一定改善。
第三次作业
前两次作业都没有对表达式进行结构化处理,导致了第三次作业表达式的存储结构必须大改。
好在表达式求导的三大难点——对输入的处理、表达式的存储结构以及化简,这次都处理得比较好——
-
对输入的处理上,有了前两次作业中采用的正则表达式加有限状态机读入的经验,修改很快;
-
表达式的存储结构上吸取了Alterego的架构(感谢Alterego!!!!),在进行重构的时候思路比较清晰,避免了第二次作业惨剧的重演;
-
化简上,层次化的表达式存储方式发挥出了它的优越性,通过统一的接口进行因子类型的转换,效果好;
在第三次作业我也首次采用了Package来管理类,也是一个小进步。
① 程序结构分析
UML类图: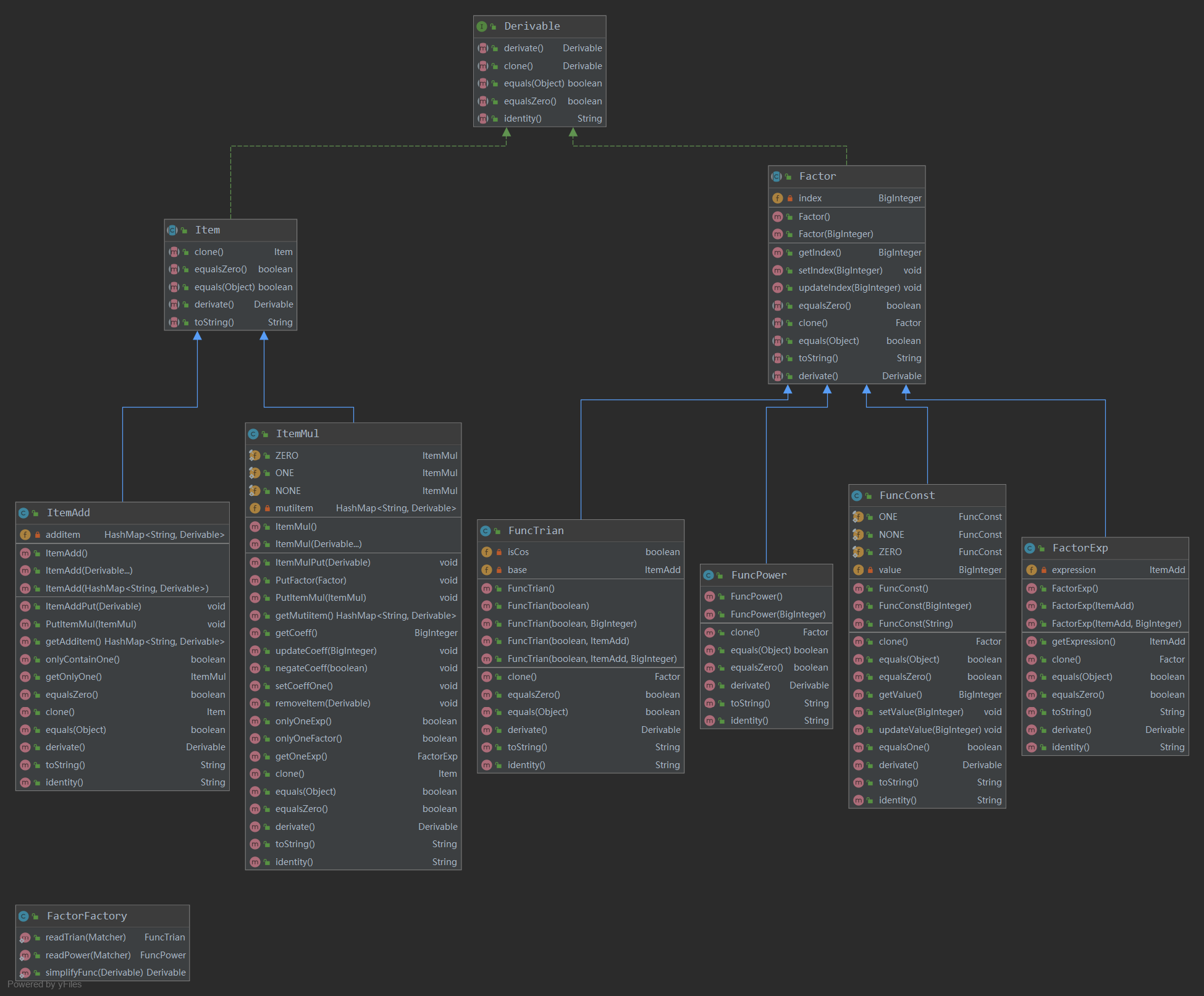
表达式解析为ItemAdd和ItemMul两层(内部有大量简化方法),以及因子,都实现了求导接口,以抽象类约束。

这一次的类图很乱,主要原因还是在于表达式也可以作为一个因子嵌套进三角函数中,类之间的相互调用也比较明显。
Method复杂度:
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| homework.MainClass.main(String[]) | 1 | 2 | 2 |
| homework.expression.ExpFunction.Exception.Exception(String) | 1 | 1 | 1 |
| homework.expression.ExpFunction.deleteSpace(String) | 3 | 7 | 10 |
| homework.expression.ExpFunction.matchParentheses(String,int) | 6 | 6 | 7 |
| homework.expression.ExpFunction.readIndex(String) | 2 | 1 | 2 |
| homework.expression.ExpFunction.simplifyExpParentheses(String) | 9 | 11 | 14 |
| homework.expression.ExpFunction.simplifyParentheses(String,int[]) | 1 | 1 | 8 |
| homework.expression.ExpFunction.simplifySign(String) | 4 | 3 | 4 |
| homework.expression.ExpParser.Exception.Exception(String) | 1 | 1 | 1 |
| homework.expression.ExpParser.ExpParser(String) | 3 | 2 | 3 |
| homework.expression.ExpParser.getItemAdd(String,boolean) | 5 | 6 | 9 |
| homework.expression.ExpParser.getItemMul(String) | 4 | 3 | 5 |
| homework.expression.ExpParser.matchParentheses() | 7 | 4 | 8 |
| homework.expression.ExpParser.readOneItem(String) | 6 | 9 | 12 |
| homework.expression.ExpParser.spliter() | 1 | 1 | 1 |
| homework.expression.ExpSimplify.ExpSimplify(Derivable) | 1 | 2 | 2 |
| homework.expression.ExpSimplify.OnlyOneDiff(Derivable,Derivable) | 9 | 17 | 26 |
| homework.expression.ExpSimplify.getDiff(boolean,int,int,ItemMul,ItemMul) | 1 | 4 | 6 |
| homework.expression.ExpSimplify.searchSimplify(ItemAdd) | 4 | 4 | 4 |
| homework.expression.ExpSimplify.simplify() | 2 | 2 | 4 |
| homework.polyitem.factor.Factor.Factor() | 1 | 1 | 1 |
| homework.polyitem.factor.Factor.Factor(BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.Factor.getIndex() | 1 | 1 | 1 |
| homework.polyitem.factor.Factor.setIndex(BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.Factor.updateIndex(BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.FactorExp.FactorExp() | 1 | 1 | 1 |
| homework.polyitem.factor.FactorExp.FactorExp(ItemAdd) | 1 | 1 | 1 |
| homework.polyitem.factor.FactorExp.FactorExp(ItemAdd,BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.FactorExp.clone() | 1 | 1 | 1 |
| homework.polyitem.factor.FactorExp.derivate() | 4 | 4 | 5 |
| homework.polyitem.factor.FactorExp.equals(Object) | 3 | 3 | 4 |
| homework.polyitem.factor.FactorExp.equalsZero() | 1 | 1 | 1 |
| homework.polyitem.factor.FactorExp.getExpression() | 1 | 1 | 1 |
| homework.polyitem.factor.FactorExp.identity() | 1 | 1 | 1 |
| homework.polyitem.factor.FactorExp.toString() | 1 | 4 | 4 |
| homework.polyitem.factor.FactorFactory.readPower(Matcher) | 1 | 2 | 2 |
| homework.polyitem.factor.FactorFactory.readTrian(Matcher) | 1 | 2 | 3 |
| homework.polyitem.factor.FactorFactory.simplifyFunc(Derivable) | 2 | 4 | 5 |
| homework.polyitem.factor.FuncConst.FuncConst() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.FuncConst(BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.FuncConst(String) | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.clone() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.derivate() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.equals(Object) | 2 | 2 | 2 |
| homework.polyitem.factor.FuncConst.equalsOne() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.equalsZero() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.getValue() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.identity() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.setValue(BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.toString() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncConst.updateValue(BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.FuncPower.FuncPower() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncPower.FuncPower(BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.FuncPower.clone() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncPower.derivate() | 1 | 1 | 2 |
| homework.polyitem.factor.FuncPower.equals(Object) | 2 | 2 | 2 |
| homework.polyitem.factor.FuncPower.equalsZero() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncPower.identity() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncPower.toString() | 1 | 1 | 2 |
| homework.polyitem.factor.FuncTrian.FuncTrian() | 1 | 1 | 1 |
| homework.polyitem.factor.FuncTrian.FuncTrian(boolean) | 1 | 1 | 1 |
| homework.polyitem.factor.FuncTrian.FuncTrian(boolean,BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.FuncTrian.FuncTrian(boolean,ItemAdd) | 1 | 1 | 1 |
| homework.polyitem.factor.FuncTrian.FuncTrian(boolean,ItemAdd,BigInteger) | 1 | 1 | 1 |
| homework.polyitem.factor.FuncTrian.clone() | 1 | 2 | 2 |
| homework.polyitem.factor.FuncTrian.derivate() | 4 | 4 | 6 |
| homework.polyitem.factor.FuncTrian.equals(Object) | 6 | 4 | 8 |
| homework.polyitem.factor.FuncTrian.equalsZero() | 3 | 3 | 4 |
| homework.polyitem.factor.FuncTrian.identity() | 1 | 4 | 5 |
| homework.polyitem.factor.FuncTrian.toString() | 1 | 2 | 3 |
| homework.polyitem.item.ItemAdd.ItemAdd() | 1 | 1 | 1 |
| homework.polyitem.item.ItemAdd.ItemAdd(Derivable...) | 1 | 3 | 3 |
| homework.polyitem.item.ItemAdd.ItemAdd(HashMap<String, Derivable>) | 1 | 1 | 1 |
| homework.polyitem.item.ItemAdd.ItemAddPut(Derivable) | 1 | 4 | 4 |
| homework.polyitem.item.ItemAdd.PutItemMul(ItemMul) | 1 | 5 | 5 |
| homework.polyitem.item.ItemAdd.clone() | 1 | 2 | 2 |
| homework.polyitem.item.ItemAdd.derivate() | 2 | 2 | 3 |
| homework.polyitem.item.ItemAdd.equals(Object) | 3 | 2 | 3 |
| homework.polyitem.item.ItemAdd.equalsZero() | 3 | 2 | 3 |
| homework.polyitem.item.ItemAdd.getAdditem() | 1 | 1 | 1 |
| homework.polyitem.item.ItemAdd.getOnlyOne() | 4 | 2 | 4 |
| homework.polyitem.item.ItemAdd.identity() | 1 | 1 | 1 |
| homework.polyitem.item.ItemAdd.onlyContainOne() | 1 | 1 | 1 |
| homework.polyitem.item.ItemAdd.toString() | 6 | 5 | 7 |
| homework.polyitem.item.ItemMul.ItemMul() | 1 | 1 | 1 |
| homework.polyitem.item.ItemMul.ItemMul(Derivable...) | 3 | 3 | 3 |
| homework.polyitem.item.ItemMul.ItemMulPut(Derivable) | 3 | 5 | 6 |
| homework.polyitem.item.ItemMul.PutFactor(Factor) | 6 | 10 | 10 |
| homework.polyitem.item.ItemMul.PutItemMul(ItemMul) | 1 | 2 | 2 |
| homework.polyitem.item.ItemMul.clone() | 1 | 2 | 2 |
| homework.polyitem.item.ItemMul.derivate() | 6 | 2 | 7 |
| homework.polyitem.item.ItemMul.equals(Object) | 3 | 2 | 3 |
| homework.polyitem.item.ItemMul.equalsZero() | 3 | 2 | 3 |
| homework.polyitem.item.ItemMul.getCoeff() | 2 | 2 | 2 |
| homework.polyitem.item.ItemMul.getMutiitem() | 1 | 1 | 1 |
| homework.polyitem.item.ItemMul.getOneExp() | 5 | 2 | 5 |
| homework.polyitem.item.ItemMul.identity() | 2 | 3 | 4 |
| homework.polyitem.item.ItemMul.negateCoeff(boolean) | 1 | 2 | 2 |
| homework.polyitem.item.ItemMul.onlyOneExp() | 3 | 3 | 7 |
| homework.polyitem.item.ItemMul.onlyOneFactor() | 4 | 3 | 7 |
| homework.polyitem.item.ItemMul.removeItem(Derivable) | 1 | 2 | 2 |
| homework.polyitem.item.ItemMul.setCoeffOne() | 1 | 1 | 1 |
| homework.polyitem.item.ItemMul.toString() | 1 | 7 | 7 |
| homework.polyitem.item.ItemMul.updateCoeff(BigInteger) | 1 | 1 | 1 |
MetricReloaded分析程序复杂度更加病态了,大量方法的结构化程度存在问题,并且集中在与化简有关的方法中。表达式解析中的readOneItem()方法三项均超标,虽然我已经进行了采用了一部分的工厂模式、将正则表达式存入单独的类中以被调用的解耦合的努力。
Package复杂度:
| Package | v(G)avg | v(G)tot |
|---|---|---|
| homework | 2 | 2 |
| homework.expression | 6.68 | 127 |
| homework.polyitem.factor | 1.86 | 93 |
| homework.polyitem.item | 3.38 | 115 |
通过分包,将几大功能区分开(不过这次看到20%的性能分,增加了暴力搜索提取公因式的简化方法,还是放在Exp处理中,所以耦合度也有点高)。
② 程序Bug分析
“OO中最惨的,不是被同屋hack了50个同质Bug,而是在截止提交的下一秒意识到了自己的Bug”
——沃茨基·硕德
在第三次作业中,我为了简化做了不少工作,也用随机数据自动测试程序做了大量的检验。然而就在周六晚上截止提交后的几秒,我突然意识到我的输出是有问题的——对于表达式因子,我将其设置为继承了Factor类,同样拥有指数Index属性,在输出时,采用的是和幂函数、三角函数一样的输出方式——“(exp)**index”,但在输入时表达式因子是不允许有指数的,因此属于WF。但对于Sympy,表达式的格式限定很宽松,通过计算并不能找到错误。
那能咋办……周六晚上看番转移注意力,周日在互测中尽可能挽回损失……最后发现强测没有出现这种输出,但互测时被同屋两名Servent发现了这个Bug。好在修复工作也比较简单,实在是侥幸。
③ 互测采用策略
在这次互测依然是采用对拍(对军宝具)+手动构造样例(我自己构造了可能会TLE的样例,也分享到了群里)+Python生成随机数据自动评测的方式。
在这次对Python生成随机数据做了优化,比如Caster在指数为0时会出现各种吊诡的错误,然而互测限定指数>0,于是我将对Caster的随机数据设为指数始终>0,其他成员照旧,避免了反复查看不能hack的Bug带来的失落感。
最后稍微吐槽一下“不优化就不会Die”,在这次互测中,房间内8名成员,4名优化输出4名不优化,最后出Bug的都是那4名优化输出的……其中Berserker还会在表达式嵌套过多时陷入死循环,截止至本文发稿时已被修好。
④ 对象创建模式
在这次的作业中终于用到了工厂模式!虽然原因是表达式解析方法太长,不得不将生成项的代码独立开来。不过我也只用工厂模式处理了幂函数、不含嵌套因子的三角函数、常数,含嵌套因子的三角函数的生成与我的状态机密切相关,难以抽象出来,这也是我的架构中的不足。
心得体会
在寒假的时候,我曾看到知乎上@HansBug学长关于OO课程改革的回答,而通过这一个多月的实际体验,OO给我的感受还是很赞的,通过互测阅读同学代码、与舍友们的交流(感谢@VOIDMalkuth!!!)、水讨论区以及学习理论课,收获很大。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号