【区间DP+二分优化】鸡蛋掉落

【题目链接】

鸡蛋掉落

【题目描述】

给你 k 枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。

已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。

每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？

【输入输出样例】

示例1：

输入：k = 1, n = 2
输出：2
解释：
　　鸡蛋从 1 楼掉落。如果它碎了，肯定能得出 f = 0 。
　　否则，鸡蛋从 2 楼掉落。如果它碎了，肯定能得出 f = 1 。
　　如果它没碎，那么肯定能得出 f = 2 。
　　因此，在最坏的情况下我们需要移动 2 次以确定 f 是多少。

 

示例 2：

输入：k = 2, n = 6

输出：3

示例3：

输入：k = 3, n = 14
输出：4
 

【数据范围】

1 <= k <= 100
1 <= n <= 10⁴

 

为了更好地理解题意，可以考虑从以下情况入手：

　　如果手上拥有无限个鸡蛋，那么对于本题来说，楼层是单调递增的，故可以使用二分的方法得出楼层 f ，所需要的步数是 O(logn)；

　　如果手上只拥有一个鸡蛋，那么就需要从一楼开始逐层往上尝试才能得出楼层f，故所需要的步数是 O(n);

　　以上两种情况的答案都是比较直观的，接下来看一种答案不那么直观的情况：

　　　　假设楼层共有 100 层，而手上仅有两个鸡蛋时，怎么做才能得出最少的步数呢？

　　　　一个比较直观的想法就是首先每 10 层进行一次尝试，当遇到某一个 10 的倍数的楼层的鸡蛋破碎了，再从上一个 10 的倍数的楼层开始往上尝试，直到找到楼层 f 为止，大致思想如下：

 

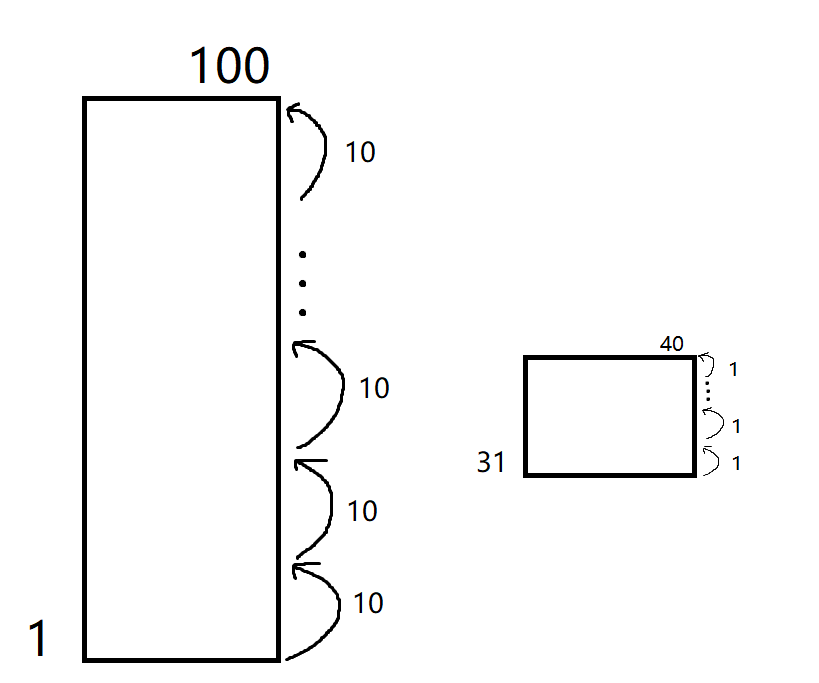
使用这种方法，可以算出最少需要的步数，也就是最坏情况下当 f = 99 时,共需要移动 19 步。

即10，20，30，40，50，60，70，80，90，100，91，92，93，94，95，96，97，98，99。

但其实仔细思考，就会发现这样的步数分配是不那么平均的，如果楼层在如 19,29,39 等这些位置的话，那么第二步需要走的次数就远大于第一步；

因此可以考虑采用不等间隔的方式来使得前后两步所走的次数尽可能地相等。

可以采用以下方案：

　　在初始时让第一步多跨越一些楼层，之后的跨度逐次减少，到最后只走一步，使得当第一步每多走一步，则第二步的所需要步数也会跟着减少。

　　通过这种方式，可以让第一步和第二步所走的步数尽量相等。

　　那么这个第一步最开始应当跨越多少楼层呢？设最开始应当跨越 n 层楼，那么可得n + (n-1) + (n-2) + (n-3) + ... + 1 >= 100，即 n >= 13.6 ，取整可得 n = 14 ，也就是第一步的路径应当是 (14,27,39,50,60,69,77,84,90,94,99,100) 。

　　这种策略的最坏情况下即是当 f = 13 时，第一步先走到14，之后第二步从1遍历到13，共14步，比上面的方案好了不少。

 

---

 

 

大致理解题意后，继续回到题目中来：

　　对于一个鸡蛋在某一楼层$k$上丢下，所能得到的仅有两种结果，就是碎与不碎。

　　如果鸡蛋碎掉，答案楼层 $f$ 就应当在$1~k$中，如果鸡蛋不碎，答案楼层 $f$ 就应当在 $k + 1 ~ n$ 中；

 

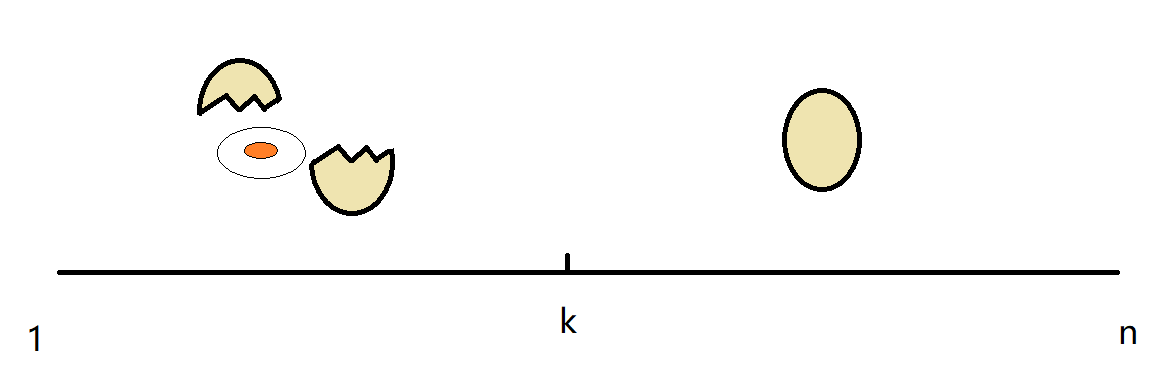
 　　显然，这是一个动态规划的问题，状态表示：$f[i,j]$表示共$i$层楼，手中拥有$j$个鸡蛋，找出答案楼层$f$的最少步数。

　　 那么当一个鸡蛋在第$k$层丢下，如果鸡蛋碎掉，那么答案就应当是$f[k - 1,j - 1] + 1$（鸡蛋少了一个，且需要加上当前这一步的操作次数一次）；

　　　　　　　　　　　　　　　　如果鸡蛋没有碎掉，那么答案就应当是$f[i - k,j] + 1$（鸡蛋数目不变，楼层转化为共有$i - k$层，手中有$j$个鸡蛋的最少步数）。

 　　显然，所要求的最小步数应当就是在第$k$层扔下鸡蛋后，这两种情况中的最大值的最小值，即$f[i,j] = min{f[i,j],max(f[k - 1,j - 1] , f[i - k,j]) + 1}$

　　 得出了状态转移方程后，问题又来了，应当在哪一层丢下鸡蛋才能获得这个最小步数呢？一种简单粗暴的思路就是枚举，枚举从$1~i$之间所有的楼层，从这些楼层中找到一个步数最小值。

　　 算一算时间复杂度，楼层共$n$层，鸡蛋共$k$个，还需要加上楼层的枚举$n$，故时间复杂度为O($kn^2$)；

　　 实现一下：

const int N = 10010,M = 110;
int f[N][M];
class Solution {
public:
    int superEggDrop(int k, int n) {
        memset(f,0,sizeof f);
        for(int i = 1;i <= n;++i)
            for(int j = 1;j <= k;++j)
                f[i][j] = i;

        for(int i = 1;i <= n;++i)
            for(int j = 2;j <= k;++j)
                for(int k = 1;k < i;++k)
                    f[i][j] = min(f[i][j],max(f[k - 1][j - 1],f[i - k][j]) + 1);
        return f[n][k];
    }
};

　　样例测完直接提交，TLE了，果然10¹⁰过不了。

接下来考虑如何优化，楼层与鸡蛋数目是无法优化的，唯一可以优化的就应当是楼层的枚举了。

回顾一下转移方程：$f[i,j] = min{f[i,j],max(f[k - 1,j - 1] , f[i - k,j]) + 1}$，这个式子希望在楼层$1~i$中找到一个楼层$k$，使得能够从$f[k - 1,j - 1] , f[i - k,j]$中选出一个最大值来更新$f[i,j]$，而为了能够让$f[i,j]$尽可能地小，这个值就应当尽可能地小。

那么就来观察一下这两个式子$f[k - 1,j - 1] , f[i - k,j]$。

对于$f[x,y]$来说，$x$是楼层数目，设鸡蛋数目$y$不变，那么当楼层$x$越高，显然所需要的步数只会与之前持平或者更多，因此可以发现$f[x,y]$在$y$不变的情况下，是随着$x$非严格递增的。

回到式子来，$f[k - 1,j - 1] , f[i - k,j]$，随着$k$的增加，$f[k-1,j-1]$应当是递增的，而$f[i - k,j]$则应当是递减的，因此可以得出下面这张图：

 

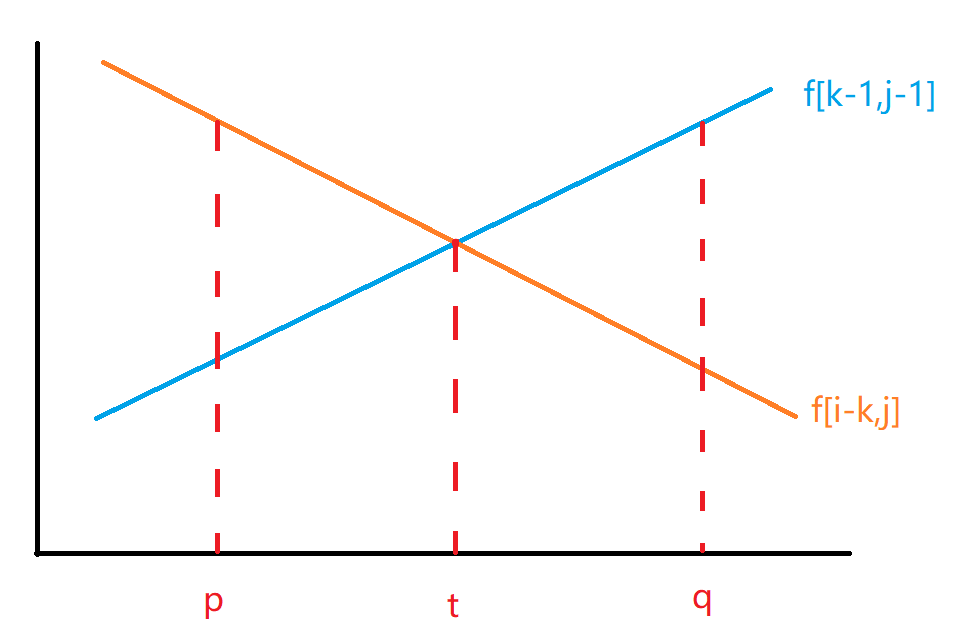
　　对于$p$点，显然有$f[i-p,j] < f[p-1,j-1]$；

　　对于$q$点，显然有$f[i-q,j] < f[q-1,j-1]$；

　　而$max(f[k - 1,j - 1] , f[i - k,j])$要找的正是点$t$，在点$t$处，能够使得$max(f[k - 1,j - 1] , f[i - k,j])$尽可能地小，以便它能够更新$f[i,j]$，但需要考虑的一点是楼层数是正整数，但点$t$并不一定是整数，不好直接求解；

　　可以考虑让点$p$和点$q$尽可能地逼近$t$，使用二分的方法找到最大的点$p$，但需要满足$f[i-p,j] <= f[p-1,j-1]$，当点$p$找到后，点$q$也自然而然地得出了，根据上述性质点$q$必然在点$p$的右侧，而为了让让点$p$和点$q$尽可能地逼近$t$，

　　点$q$要么恰好等于点$p$，要么就在$p$的下一个位置，即$p+1=q$。

　　确定思路后，代码的实现比较简单，使用二分的板子即可。时间复杂度也将为了O($knlogn$)。

　　

const int N = 10010,M = 110;
int f[N][M];
class Solution {
public:
    int superEggDrop(int k, int n) {
        memset(f,0,sizeof f);
        for(int i = 1;i <= n;++i)
            for(int j = 1;j <= k;++j)
                f[i][j] = i;

        for(int i = 1;i <= n;++i)
            for(int j = 2;j <= k;++j)
            {
                // for(int k = 1;k < i;++k)
                //     f[i][j] = min(f[i][j],max(f[k - 1][j - 1],f[i - k][j]) + 1);
                int l = 1,r = i;
                while(l < r)
                {
                    int mid = l + r + 1 >> 1;
                    if(f[mid - 1][j - 1] <= f[i - mid][j])
                        l = mid;
                    else
                        r = mid - 1;
                }
                int t = max(f[l - 1][j - 1],f[i - l][j]);
                if(l + 1 <= k)  t = max(t,max(f[r - 1][j - 1],f[i - r][j]));
                f[i][j] = min(f[i][j],t + 1);
            }
        return f[n][k];
    }
};