牛客小白月赛14 B.投硬币

 

通过数学原理推公式 ，可得：
有k次成功的概率为：C(n,k) * p^k * (1-p)^(n-k)
有k+1次成功的概率为：C(n,k+1) * p^(k+1) * (1-p)^(n-k-1)
……
有n次成功的概率为：C(n,n) * p^n * (1-p)^0

这里我们很容易推出每一种情况的公式：
C(n,i) * p^i * (1-p)^(n-i)

然后将 k — n 的每一项加起来，求得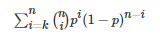  

#include<bits/stdc++.h>
using namespace std;
#define maxn 300005
#define ll long long
const ll mod = 998244353;

ll n,k,p,sum;
ll pri[maxn],ni[maxn];

ll poww(ll a,ll b){
    ll ans=1,base=a;
    while(b!=0){
        if(b&1!=0)ans=(ans*base)%mod;
        base=(base*base)%mod;
        b>>=1;
    }
    return ans%mod;
}

void s(){
    pri[0]=ni[0]=1;
    for(int i=1;i<=n;i++){
        pri[i]=pri[i-1]*i%mod;
        ni[i]=poww(pri[i],mod-2);
    }
}

int main()
{
    scanf("%lld %lld %lld",&n,&k,&p);
    s();
    for(int i=k;i<=n;i++){
        sum+=pri[n]*ni[n-i]%mod*ni[i]%mod*poww(p,i)%mod*poww((1-p+mod)%mod,n-i)%mod;
        sum%=mod;
    }
    printf("%lld",sum);
    return 0;
}