刷题碎碎念---力扣001-006

001--两数之和

比较简单，暴力法就能过，可以用HashMap优化一下

class Solution {
    public int[] twoSum(int[] nums, int target) {
       HashMap<Integer,Integer> maps = new HashMap<Integer,Integer>();

       for(int i=0; i<nums.length; i++){
           if(maps.containsKey(target - nums[i])){
               int j = maps.get(target-nums[i]);
               return new int[]{i,j};
           }

           maps.put(nums[i],i);
       }

       return new int[0];
    }
}

002---两数相加

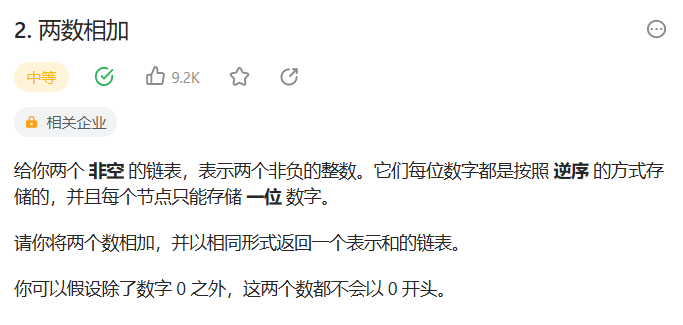
比较简单吧，就是一个链表的遍历，然后手动进行一个加法，没啥难度，就是注意一下最后那个进位就行了。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode head = new ListNode();

        ListNode node;
        node = head;

        int flag = 0;
        while(l1 != null || l2 != null){
            
            int i = l1 != null ? l1.val : 0;
            int j = l2 != null ? l2.val : 0;

            int num = i + j + flag;
            flag = 0; // 进位标志
            if (num >= 10){
                flag = 1;
                num %= 10;
            }
            node.next = new ListNode(num);
            node = node.next;
            l1 = l1 != null ? l1.next : null;
            l2 = l2 != null ? l2.next : null;
        }

        if(flag == 1) node.next = new ListNode(flag);

        return head.next;
    }
}

003 --- 最长子串

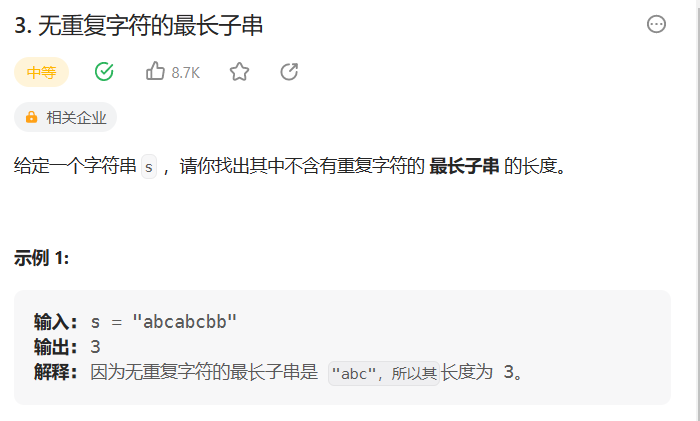
用了一个类似dp的思想，就是从第一位开始计算最长的无重复子序列，然后第二位可以在第一位的基础上进行计算，减少计算次数。

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s.length() <= 1) return s.length();

        Set<Character> occ = new HashSet<Character>();
        int maxLen = 0; // 最大长度
        int index = 1; // 下标
        occ.add(s.charAt(0));
        for(int i=1; i<s.length(); i++){
            while(index < s.length() && ! occ.contains(s.charAt(index))){
                occ.add(s.charAt(index++));
            }
            occ.remove(s.charAt(i-1));
            maxLen = Math.max(maxLen,index - i + 1);
            if(index == s.length()) return maxLen;
        }

        return maxLen;
    }
}

004 --- 寻找两个正序数组的中位数

用了一个类似于二分查找一样的算法，就是将完全不可能的数据给舍弃掉就行了。建立了一个递归方法，用于寻找第k位的数，然后因为两个数列是有序的，所以可以对k/2-1处的数据大小进行判断，然后如果谁更小就肯定不可能是第k位，然后可以完全舍弃掉。接着进行递归。

代码中的递归方法是我自己琢磨出来的，感觉还算优雅。

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int k = nums1.length + nums2.length;
        if(k % 2 == 0){
            return ((findKSortedArrays(nums1,nums2,0,0,k / 2 + 1) + findKSortedArrays(nums1,nums2,0,0,k / 2)) / 2);
        }else{
            return findKSortedArrays(nums1,nums2,0,0,k / 2 + 1);
        }
        
    }

    public double findKSortedArrays(int[] nums1, int[] nums2,int start1,int start2,int k) {
        if(start1 >= nums1.length) return nums2[start2 + k-1];
        if(start2 >= nums2.length) return nums1[start1 + k-1];
        if (k <= 1){
            return Math.min(nums1[start1],nums2[start2]); 
        }
        
        int index1 = Math.min(k/2 - 1,nums1.length - start1 - 1);
        int index2 = Math.min(k/2 - 1,nums2.length - start2 - 1);

        if(nums1[start1 + index1] <= nums2[start2 + index2]){
            k -= (index1 + 1);
            start1 += (index1 + 1);
        }else{
            k -= (index2 + 1);
            start2 += (index2 + 1);
        }

        return findKSortedArrays(nums1,nums2,start1,start2,k);
    }
}

005 --- 最长回文子串

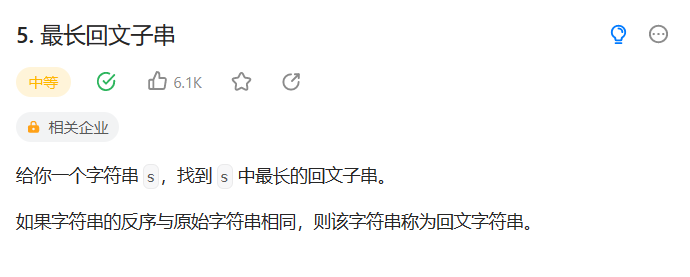
典型的dp题，没啥好说的

class Solution {
    public String longestPalindrome(String s) {
        if(s.length() == 1) return s;
        int x=0,y=0;
        boolean[][] dp = new boolean[s.length()][s.length()];
        for(int i=1; i<=s.length(); i++){
            for(int j=0; j<=s.length()-i; j++){
                if(i == 1){
                    dp[j][j] = true;
                }
                else if(i == 2 && s.charAt(j) == s.charAt(j+1)){
                    dp[j][j+1] = true;
                    x = j;
                    y = j + 1;
                }
                else{
                    if(dp[j+1][j+i-2] == true && s.charAt(j) == s.charAt(j+i-1)){
                        dp[j][j+i-1] = true;
                        x = j;
                        y = j+i-1;      
                    }
                }
            }
        }
        return s.substring(x,y + 1);
    }
}

006 --- N字形变换

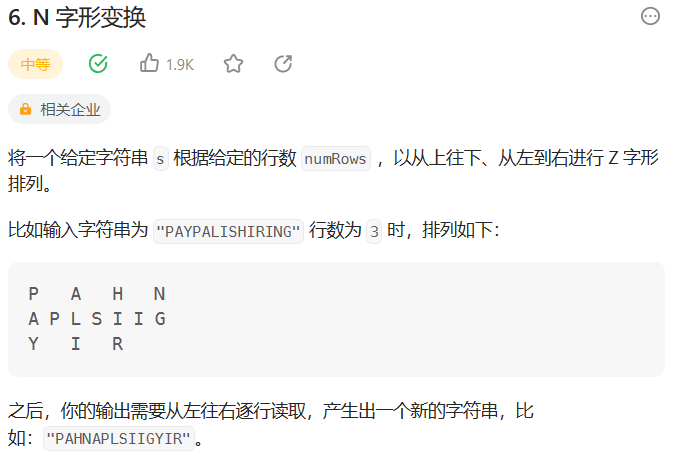
就是一个标记问题，例如：为4时，进行1234321，然后将同类型的放在同一个字符串中即可
代码中的flag和mark的使用是我第一次这么用。

class Solution {
    public String convert(String s, int numRows) {
        if(numRows < 2) return s;
        StringBuilder[] rows = new StringBuilder[numRows];

        int flag = 1;
        int mark = 0;
        for(int i=0; i<numRows; i++) rows[i] = new StringBuilder();
        for(int i=0; i< s.length(); i++) {
            rows[mark].append(s.charAt(i));
            mark += flag;
            if(mark == 0 || mark == numRows-1) flag = -flag;
        }

        StringBuilder result = new StringBuilder();
        for(StringBuilder row : rows){
            result.append(row);
        }

        return result.toString();
    }
}