003-sarsa
本学习笔记转自https://morvanzhou.github.io/
什么是 Sarsa
今天我们会来说说强化学习中一个和 Q learning 类似的算法, 叫做 Sarsa.
注: 本文不会涉及数学推导. 大家可以在很多其他地方找到优秀的数学推导文章.
在强化学习中 Sarsa 和 Q learning 及其类似, 这节内容会基于之前我们所讲的 Q learning. 所以还不熟悉 Q learning 的朋友们, 请前往我制作的 Q learning 简介 (知乎专栏). 我们会对比 Q learning, 来看看 Sarsa 是特殊在哪些方面. 和上次一样, 我们还是使用写作业和看电视这个例子. 没写完作业去看电视被打, 写完了作业有糖吃.
Sarsa 决策

Sarsa 的决策部分和 Q learning 一模一样, 因为我们使用的是 Q 表的形式决策, 所以我们会在 Q 表中挑选值较大的动作值施加在环境中来换取奖惩. 但是不同的地方在于 Sarsa 的更新方式是不一样的.
Sarsa 更新行为准则
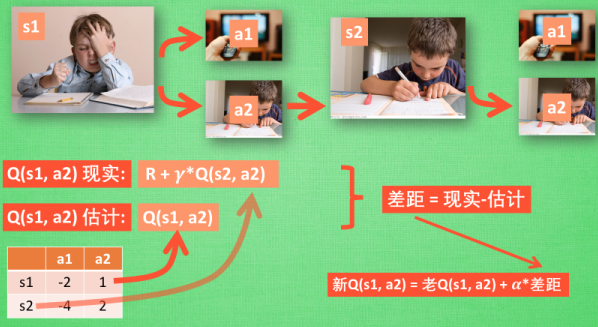
同样, 我们会经历正在写作业的状态 s1, 然后再挑选一个带来最大潜在奖励的动作 a2, 这样我们就到达了 继续写作业状态 s2, 而在这一步, 如果你用的是 Q learning, 你会观看一下在 s2 上选取哪一个动作会带来最大的奖励, 但是在真正要做决定时, 却不一定会选取到那个带来最大奖励的动作, Q-learning 在这一步只是估计了一下接下来的动作值. 而 Sarsa 是实践派, 他说到做到, 在 s2 这一步估算的动作也是接下来要做的动作. 所以 Q(s1, a2) 现实的计算值, 我们也会稍稍改动, 去掉maxQ, 取而代之的是在 s2 上我们实实在在选取的 a2 的 Q 值. 最后像 Q learning 一样, 求出现实和估计的差距 并更新 Q 表里的 Q(s1, a2).
对比 Sarsa 和 Q-learning 算法

从算法来看, 这就是他们两最大的不同之处了. 因为 Sarsa 是说到做到型, 所以我们也叫他 on-policy, 在线学习, 学着自己在做的事情. 而 Q learning 是说到但并不一定做到, 所以它也叫作 Off-policy, 离线学习. 而因为有了 maxQ, Q-learning 也是一个特别勇敢的算法.

为什么说他勇敢呢, 因为 Q learning 机器人 永远都会选择最近的一条通往成功的道路, 不管这条路会有多危险. 而 Sarsa 则是相当保守, 他会选择离危险远远的, 拿到宝藏是次要的, 保住自己的小命才是王道. 这就是使用 Sarsa 方法的不同之处.
Sarsa 算法更新
要点
这次我们用同样的迷宫例子来实现 RL 中另一种和 Qlearning 类似的算法, 叫做 Sarsa (state-action-reward-state_-action_). 我们从这一个简称可以了解到, Sarsa 的整个循环都将是在一个路径上, 也就是 on-policy, 下一个 state_, 和下一个 action_ 将会变成他真正采取的 action 和 state. 和 Qlearning 的不同之处就在这. Qlearning 的下个一个 state_ action_ 在算法更新的时候都还是不确定的 (off-policy). 而 Sarsa 的 state_, action_ 在这次算法更新的时候已经确定好了 (on-policy).
算法

整个算法还是一直不断更新 Q table 里的值, 然后再根据新的值来判断要在某个 state 采取怎样的 action. 不过于 Qlearning 不同之处:
- 他在当前
state已经想好了state对应的action, 而且想好了 下一个state_和下一个action_(Qlearning 还没有想好下一个action_) - 更新
Q(s,a)的时候基于的是下一个Q(s_, a_)(Qlearning 是基于maxQ(s_))
这种不同之处使得 Sarsa 相对于 Qlearning, 更加的胆小. 因为 Qlearning 永远都是想着 maxQ 最大化, 因为这个 maxQ 而变得贪婪, 不考虑其他非 maxQ 的结果. 我们可以理解成 Qlearning 是一种贪婪, 大胆, 勇敢的算法, 对于错误, 死亡并不在乎. 而 Sarsa 是一种保守的算法, 他在乎每一步决策, 对于错误和死亡比较铭感. 这一点我们会在可视化的部分看出他们的不同. 两种算法都有他们的好处, 比如在实际中, 你比较在乎机器的损害, 用一种保守的算法, 在训练时就能减少损坏的次数.
算法的代码形式
首先我们先 import 两个模块, maze_env 是我们的环境模块, 已经编写好了, 大家可以直接在这里下载, maze_env 模块我们可以不深入研究, 如果你对编辑环境感兴趣, 可以去看看如何使用 python 自带的简单 GUI 模块 tkinter 来编写虚拟环境. 我也有对应的教程. maze_env 就是用 tkinter 编写的. 而 RL_brain 这个模块是 RL 的大脑部分, 我们下节会讲.
from maze_env import Maze from RL_brain import SarsaTable
下面的代码, 我们可以根据上面的图片中的算法对应起来, 这就是整个 Sarsa 最重要的迭代更新部分啦.
def update(): for episode in range(100): # 初始化环境 observation = env.reset() # Sarsa 根据 state 观测选择行为 action = RL.choose_action(str(observation)) while True: # 刷新环境 env.render() # 在环境中采取行为, 获得下一个 state_ (obervation_), reward, 和是否终止 observation_, reward, done = env.step(action) # 根据下一个 state (obervation_) 选取下一个 action_ action_ = RL.choose_action(str(observation_)) # 从 (s, a, r, s, a) 中学习, 更新 Q_tabel 的参数 ==> Sarsa RL.learn(str(observation), action, reward, str(observation_), action_) # 将下一个当成下一步的 state (observation) and action observation = observation_ action = action_ # 终止时跳出循环 if done: break # 大循环完毕 print('game over') env.destroy() if __name__ == "__main__": env = Maze() RL = SarsaTable(actions=list(range(env.n_actions))) env.after(100, update) env.mainloop()
Sarsa 思维决策
接着上节内容, 我们来实现 RL_brain 的 SarsaTable 部分, 这也是 RL 的大脑部分, 负责决策和思考.
代码主结构
和之前定义 Qlearning 中的 QLearningTable 一样, 因为使用 tabular 方式的 Sarsa 和 Qlearning 的相似度极高,
class SarsaTable:
# 初始化 (与之前一样)
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
# 选行为 (与之前一样)
def choose_action(self, observation):
# 学习更新参数 (有改变)
def learn(self, s, a, r, s_):
# 检测 state 是否存在 (与之前一样)
def check_state_exist(self, state):
我们甚至可以定义一个 主class RL, 然后将 QLearningTable 和 SarsaTable 作为 主class RL 的衍生, 这个主 RL 可以这样定义. 所以我们将之前的 __init__, check_state_exist, choose_action, learn 全部都放在这个主结构中, 之后根据不同的算法更改对应的内容就好了.
import numpy as np
import pandas as pd
class RL(object):
def __init__(self, action_space, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
... # 和 QLearningTable 中的代码一样
def check_state_exist(self, state):
... # 和 QLearningTable 中的代码一样
def choose_action(self, observation):
... # 和 QLearningTable 中的代码一样
def learn(self, *args):
pass # 每种的都有点不同, 所以用 pass
如果是这样定义父类的 RL class, 通过继承关系, 那之子类 QLearningTable class 就能简化成这样:
class QLearningTable(RL): # 继承了父类 RL
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
super(QLearningTable, self).__init__(actions, learning_rate, reward_decay, e_greedy) # 表示继承关系
def learn(self, s, a, r, s_): # learn 的方法在每种类型中有不一样, 需重新定义
self.check_state_exist(s_)
q_predict = self.q_table.loc[s, a]
if s_ != 'terminal':
q_target = r + self.gamma * self.q_table.loc[s_, :].max()
else:
q_target = r
self.q_table.loc[s, a] += self.lr * (q_target - q_predict)
学习
有了父类的 RL, 我们这次的编写就很简单, 只需要编写 SarsaTable 中 learn 这个功能就完成了. 因为其他功能都和父类是一样的. 这就是我们所有的 SarsaTable 于父类 RL 不同之处的代码. 是不是很简单.
class SarsaTable(RL): # 继承 RL class
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
super(SarsaTable, self).__init__(actions, learning_rate, reward_decay, e_greedy) # 表示继承关系
def learn(self, s, a, r, s_, a_):
self.check_state_exist(s_)
q_predict = self.q_table.loc[s, a]
if s_ != 'terminal':
q_target = r + self.gamma * self.q_table.loc[s_, a_] # q_target 基于选好的 a_ 而不是 Q(s_) 的最大值
else:
q_target = r # 如果 s_ 是终止符
self.q_table.loc[s, a] += self.lr * (q_target - q_predict) # 更新 q_table
什么是 Sarsa(lambda)
今天我们会来说说强化学习中基于 Sarsa 的一种提速方法, 叫做 sarsa-lambda.
Sarsa(n)
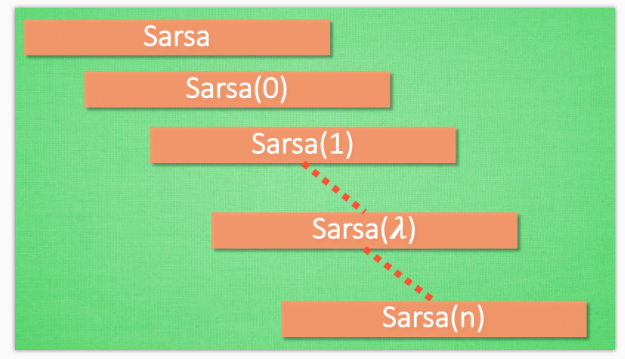
通过上个视频的介绍, 我们知道这个 [Sarsa]/tutorials/machine-learning/ML-intro/4-04-sarsa/)) 的算法是一种在线学习法, on-policy. 但是这个 lambda 到底是什么. 其实吧, Sarsa 是一种单步更新法, 在环境中每走一步, 更新一次自己的行为准则, 我们可以在这样的 Sarsa 后面打一个括号, 说他是 Sarsa(0), 因为他等走完这一步以后直接更新行为准则. 如果延续这种想法, 走完这步, 再走一步, 然后再更新, 我们可以叫他 Sarsa(1). 同理, 如果等待回合完毕我们一次性再更新呢, 比如这回合我们走了 n 步, 那我们就叫 Sarsa(n). 为了统一这样的流程, 我们就有了一个 lambda 值来代替我们想要选择的步数, 这也就是 Sarsa(lambda) 的由来. 我们看看最极端的两个例子, 对比单步更新和回合更新, 看看回合更新的优势在哪里.
单步更新 and 回合更新
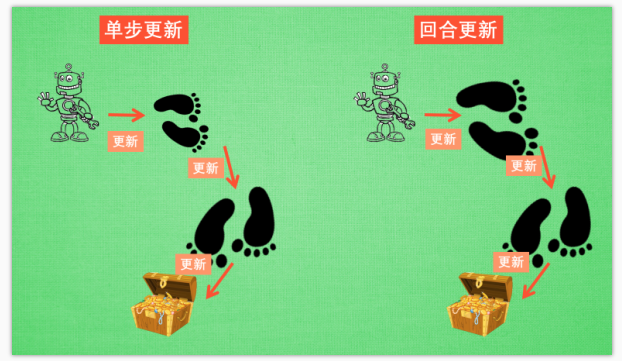
虽然我们每一步都在更新, 但是在没有获取宝藏的时候, 我们现在站着的这一步也没有得到任何更新, 也就是直到获取宝藏时, 我们才为获取到宝藏的上一步更新为: 这一步很好, 和获取宝藏是有关联的, 而之前为了获取宝藏所走的所有步都被认为和获取宝藏没关系. 回合更新虽然我要等到这回合结束, 才开始对本回合所经历的所有步都添加更新, 但是这所有的步都是和宝藏有关系的, 都是为了得到宝藏需要学习的步, 所以每一个脚印在下回合被选则的几率又高了一些. 在这种角度来看, 回合更新似乎会有效率一些.
有时迷茫
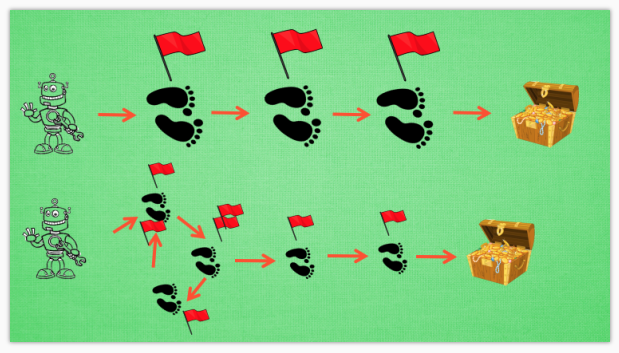
我们看看这种情况, 还是使用单步更新的方法在每一步都进行更新, 但是同时记下之前的寻宝之路. 你可以想像, 每走一步, 插上一个小旗子, 这样我们就能清楚的知道除了最近的一步, 找到宝物时还需要更新哪些步了. 不过, 有时候情况可能没有这么乐观. 开始的几次, 因为完全没有头绪, 我可能在原地打转了很久, 然后才找到宝藏, 那些重复的脚步真的对我拿到宝藏很有必要吗? 答案我们都知道. 所以Sarsa(lambda)就来拯救你啦.
Lambda 含义
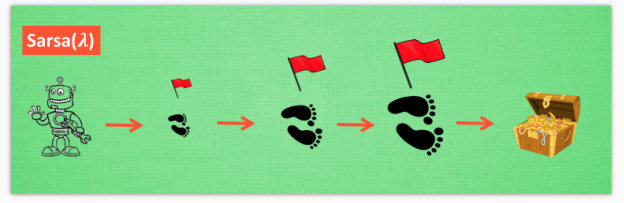
其实 lambda 就是一个衰变值, 他可以让你知道离奖励越远的步可能并不是让你最快拿到奖励的步, 所以我们想象我们站在宝藏的位置, 回头看看我们走过的寻宝之路, 离宝藏越近的脚印越看得清, 远处的脚印太渺小, 我们都很难看清, 那我们就索性记下离宝藏越近的脚印越重要, 越需要被好好的更新. 和之前我们提到过的 奖励衰减值 gamma 一样, lambda 是脚步衰减值, 都是一个在 0 和 1 之间的数.
Lambda 取值
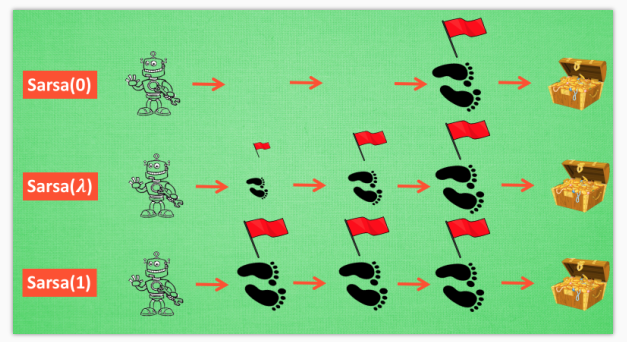
当 lambda 取0, 就变成了 Sarsa 的单步更新, 当 lambda 取 1, 就变成了回合更新, 对所有步更新的力度都是一样. 当 lambda 在 0 和 1 之间, 取值越大, 离宝藏越近的步更新力度越大. 这样我们就不用受限于单步更新的每次只能更新最近的一步, 我们可以更有效率的更新所有相关步了.
Sarsa-lambda
要点
Sarsa-lambda 是基于 Sarsa 方法的升级版, 他能更有效率地学习到怎么样获得好的 reward. 如果说 Sarsa 和 Qlearning 都是每次获取到 reward, 只更新获取到 reward 的前一步. 那 Sarsa-lambda 就是更新获取到 reward 的前 lambda 步. lambda 是在 [0, 1] 之间取值,
如果 lambda = 0, Sarsa-lambda 就是 Sarsa, 只更新获取到 reward 前经历的最后一步.
如果 lambda = 1, Sarsa-lambda 更新的是 获取到 reward 前所有经历的步.
这样解释起来有点抽象, 还是建议大家观看我制作的 什么是 Sarsa-lambda 短视频, 用动画展示具体的区别.
代码主结构
使用 SarsaLambdaTable 在算法更新迭代的部分, 是和之前的 SarsaTable 一样的, 所以这一节, 我们没有算法更新部分, 直接变成 思维决策部分.
class SarsaLambdaTable:
# 初始化 (有改变)
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9, trace_decay=0.9):
# 选行为 (与之前一样)
def choose_action(self, observation):
# 学习更新参数 (有改变)
def learn(self, s, a, r, s_):
# 检测 state 是否存在 (有改变)
def check_state_exist(self, state):
同样, 我们选择继承的方式, 将 SarsaLambdaTable 继承到 RL, 所以我们将之前的 __init__, check_state_exist, choose_action, learn 全部都放在这个主结构中, 之后根据不同的算法更改对应的内容就好了. 所以还没弄懂这些功能的朋友们, 请回到之前的教程再看一遍.
算法的相应更改请参考这个:

预设值
在预设值当中, 我们添加了 trace_decay=0.9 这个就是 lambda 的值了. 这个值将会使得拿到 reward 前的每一步都有价值. 如果还不太明白其他预设值的意思, 请查看我的 关于强化学习的短视频列表
class SarsaLambdaTable(RL): # 继承 RL class
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9, trace_decay=0.9):
super(SarsaLambdaTable, self).__init__(actions, learning_rate, reward_decay, e_greedy)
# 后向观测算法, eligibility trace.
self.lambda_ = trace_decay
self.eligibility_trace = self.q_table.copy() # 空的 eligibility trace 表
检测 state 是否存在
check_state_exist 和之前的是高度相似的. 唯一不同的地方是我们考虑了 eligibility_trace,
class SarsaLambdaTable(RL): # 继承 RL class
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9, trace_decay=0.9):
...
def check_state_exist(self, state):
if state not in self.q_table.index:
# append new state to q table
to_be_append = pd.Series(
[0] * len(self.actions),
index=self.q_table.columns,
name=state,
)
self.q_table = self.q_table.append(to_be_append)
# also update eligibility trace
self.eligibility_trace = self.eligibility_trace.append(to_be_append)
学习
有了父类的 RL, 我们这次的编写就很简单, 只需要编写 SarsaLambdaTable 中 learn 这个功能就完成了. 因为其他功能都和父类是一样的. 这就是我们所有的 SarsaLambdaTable 于父类 RL 不同之处的代码. 是不是很简单.
class SarsaLambdaTable(RL): # 继承 RL class
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9, trace_decay=0.9):
...
def check_state_exist(self, state):
...
def learn(self, s, a, r, s_, a_):
# 这部分和 Sarsa 一样
self.check_state_exist(s_)
q_predict = self.q_table.ix[s, a]
if s_ != 'terminal':
q_target = r + self.gamma * self.q_table.ix[s_, a_]
else:
q_target = r
error = q_target - q_predict
# 这里开始不同:
# 对于经历过的 state-action, 我们让他+1, 证明他是得到 reward 路途中不可或缺的一环
self.eligibility_trace.ix[s, a] += 1
# Q table 更新
self.q_table += self.lr * error * self.eligibility_trace
# 随着时间衰减 eligibility trace 的值, 离获取 reward 越远的步, 他的"不可或缺性"越小
self.eligibility_trace *= self.gamma*self.lambda_
除了图中和上面代码这种更新方式, 还有一种会更加有效率. 我们可以将上面的这一步替换成下面这样:
# 上面代码中的方式: self.eligibility_trace.ix[s, a] += 1 # 更有效的方式: self.eligibility_trace.ix[s, :] *= 0 self.eligibility_trace.ix[s, a] = 1
他们两的不同之处可以用这张图来概括:
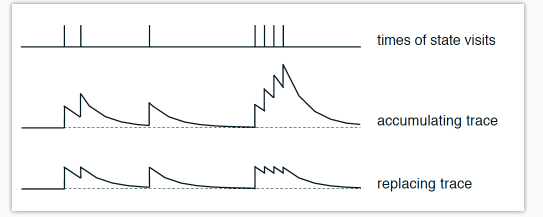
这是针对于一个 state-action 值按经历次数的变化. 最上面是经历 state-action 的时间点, 第二张图是使用这种方式所带来的 “不可或缺性值”:
self.eligibility_trace.ix[s, a] += 1
下面图是使用这种方法带来的 “不可或缺性值”:
self.eligibility_trace.ix[s, :] *= 0; self.eligibility_trace.ix[s, a] = 1
实验证明选择下面这种方法会有更好的效果. 大家也可以自己玩一玩, 试试两种方法的不同表现.
最后不要忘了, eligibility trace 只是记录每个回合的每一步, 新回合开始的时候需要将 Trace 清零.
for episode in range(100):
...
# 新回合, 清零
RL.eligibility_trace *= 0
while True: # 开始回合
...



 浙公网安备 33010602011771号
浙公网安备 33010602011771号