005-HMM隐马尔可夫链
马尔可夫链,因安德烈·马尔可夫(A.A.Markov,1856-1922)得名,是指数学中具有马尔科夫性质的离散随机过程。
在给定当前知识或信息的情况下,过去(即当前以前的历史状态)对于预测将来(即当前以后的未来状态)是无关的。

每个状态的转移,只依赖于之前的n个状态,这个过程被称为1个n阶的模型。其中n是影响转移状态的数目。
最简单的马尔可夫过程是一阶过程。每一个状态的转移只是依赖于之前的那一个状态。用数学表达式表示就是下面的样子。
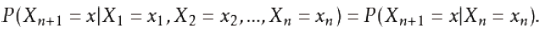
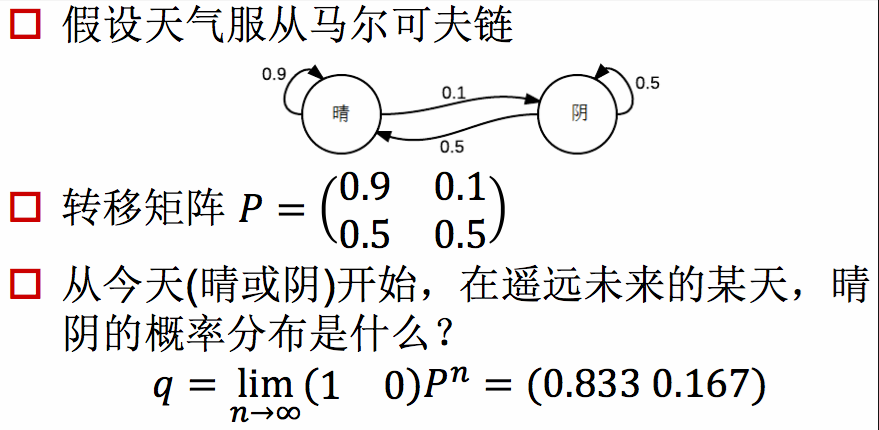

至此我们就为上面的一阶马尔可夫过程定义了以下三个部分。
1.状态:晴天、阴天。
2.初始向量:定义系统在时间为0的是偶的状态的概率。
3.状态转移矩阵:每种天气转换的概率。所有的可能被这样描述的的系统都是一个马尔可夫过程。
马尔可夫链的缺陷:
很明显,前后关系的缺失,带来了信息的缺失:
比如我们的股市,如果只是观测市场,我们只能知道当天的价格、成交量等信息,但是并不知道当前股市处于什么样的状态
(牛市、熊市、震荡、反弹等等),在这种情况下,我们有两个状态集合,一个可以观察到的状态集合。
(股市价格成交量状态等)和一个隐藏的状态集合(股市状况)。
我们希望能找到一个算法,可以根据股市价格成交量状态和马尔科夫假设来预测股市的状况。
在上面这些情况下,可以观察到的状态序列和隐藏的状态序列是概率相关的。
于是我们可以将这种类型的过程建模为有一个隐藏的马尔可夫过程和一个隐藏马尔可夫过程概率相关的,并且可以管擦到的状态集合。
就是隐马尔科夫模型。
隐马尔可夫链:
隐马尔可夫链(Hidden Markov Model)是一种统计模型:
用来描述一个含有隐含位置参数的马尔科夫过程。
其难点是从可观察的参数中确定隐含参数。
然后利用这些参数来做进一步的分析。

投掷3次骰子,每次随机抽取一个骰子
可观测到的是1-8,如果我不知道投掷的是哪个一骰子,以及每次抽取的是哪一个骰子。
那么每次抽取到D6,D4,D8的概率就是隐藏的马尔科夫链。

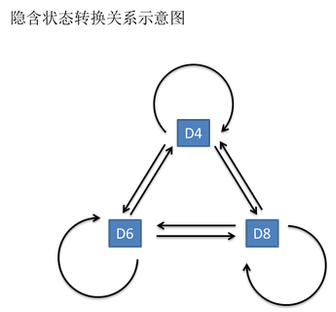
隐马尔可夫链的三大问题:
1.知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据投掷骰子的结果(可见状态链),我们想知道每次投注来的那种骰子(隐含状态链)
2.还是知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据投掷骰子出的结果(可见状态链),我们想知道投掷出这个结果的概率。
3.知道骰子有几种(隐含状态数量),不知道每种骰子是什么(转换概率),观测到很多投掷骰子的结果(可见状态链),我想反推出每种骰子是什么(转换概率)。

O:可观察到的序列
A:状态转移矩阵
B:观测出的分布概率
π:初始分布概率
Q:中间状态
课堂问答:
初始概率分布:π
状态转移矩阵:A
观测量的概率分布:B
同时有2个状态rainy,sunny
三种可能的观测值:walk,shop,clean
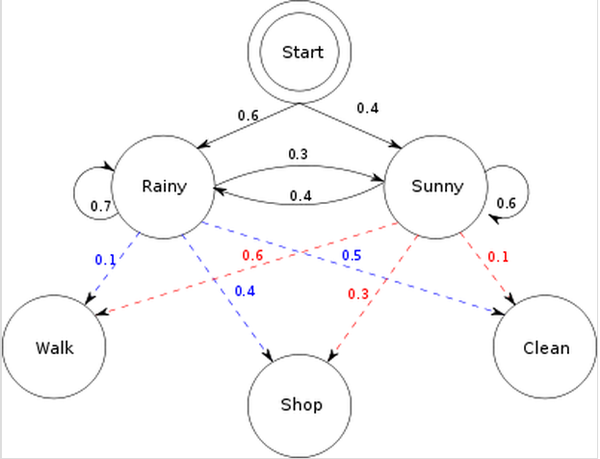
初始概率分布π:start
\begin{bmatrix}
0.6 &0.4
\end{bmatrix}
状态转移矩阵A:rainy,sunny
\begin{bmatrix}
0.7 &0.3 \\
0.6&0.4
\end{bmatrix}
观测量的概率分布B:walk,shop,clean
\begin{bmatrix}
0.1 &0.4 &0.5 \\
0.6 & 0.3 &0.1
\end{bmatrix}
问题1:已知整个模型,我们观测到连续三天做的事情是:散步,购物,收拾。那么,根据模型,计算产生这些行为的概率是多少。(已知模型,求观测概率)
问题2:同样知晓这个模型,同样是这三件事,我想猜一下,这三天的天气是怎么样的?(已知模型,求状态转换矩阵)
问题3:最复杂的,我知道这3天做了3件事,而其他什么信息也没有。我得建立一个模型,晴雨转换概率,第一天天气情况的概率分布。根据天机情况选择做某事的概率分布。(求初始概率,转换矩阵,根据实际值建模)
隐马尔可夫的解法:
问题1:遍历算法;Forward Algorithm,向前算法;或者Backward Algo,向后算法。
问题2:Viterbi Algo ,维特比算法。
问题3:Baum-Welch Algo,鲍姆-韦尔奇算法。
问题1:遍历算法;


就是根据模型,把所有的可能性相乘
如果计算P(R,R,R,W,S,C)三天下雨,分别是W,S,C的行为的概率:
就是:0.6*0.1*0.7*0.4*0.7*0.5
问题1:Forward Algorithm,向前算法;

就是将模型看成时间单位,按照时间单位进行一步一步的计算:
t =1,W的概率:
P(W,R)=P(1R)*P(W|R)=0.6*0.1=0.06 #第一天下雨跑步的概率
P(W,S)=P(1S)*P(W|S)=0.4*0.6=0.24 #第一天晴天跑步的概率
t =2,Shoping的概率,基于上一步的计算结果
P(1W,2S,2R) = [ #第一天跑步,第二天购物,第二天下雨
P(1W,1R)*P(2R|1R)+ #第一天跑步又下雨*第一天下雨第二天也下雨
P(1W,1S)*P(2R|1S) #第一天跑步又是晴天*第一天晴天且第二天下雨
]*P(2S,2R) #第2天购物,第二天下雨
问题1:Backward Algo,向后算法:

将后向某个观测点设为概率1
t = 3
β(3R) = 1
β(3S) = 1
递推:
β(2R) = a(R→R)*b(R)(3O =C)*β(3R) + #前一天下雨后一天也下雨的概率*后一天下雨行为是C的概率的喷射值(喷射值就是发生的概率,英文版公式写的是喷射值)
a(R→S)*b(S)*(3O =C)*β(3S) #前一天下雨后一天晴天的概率*后一天晴天行为是C的喷射值
=0.7*0.5*1+
0.3*0.1*1
问题2,Viterbi算法

遍历所有路径获得最大值
δ1(R) = π(R)*b(R,O1=W) #初始值下雨且第一天跑步的概率
δ1(S) = π(S)*b(S,O1=W) #初始值晴天且第一天跑步的概率
路径变量:
φ1(R) = 0
φ2(S) = 0
δ2(R) =max[δ1(R)*a(R→R),δ1(S)*a(S→R)]b(R,O2 = S) #第2天下雨的概率 = max[第1天下雨的概率*前一天下雨且后一天下雨的概率,第1天晴天的概率*前一天晴天后一天下雨的概率]*第二天下雨且O2是Shopping的概率
δ2(S) =max[δ1(S)*a(R→S),δ1(R)*a(S→S)]b(S,O2 = S) #第2天天晴的概率 = max[第1天晴天的概率*前一天下雨且后一天天晴的概率,第1天下雨的概率*前一天晴天后一天晴天的概率]*第二天晴天且O2是Shopping的概率
路径变量:
φ2(R) = max[δ1(R)and δ2(R),δ1(S) and δ2(R)] #选取由δ1到δ2使得δ2最大的路径
φ2(S) = max[δ1(R)and δ2(S),δ1(S) and δ2(S)] #同上
记录前一步使我这一步最好的结果,以此类推
问题3:Baum-Welch算法

ε表示中间状态从i(t = t)到j(t = t+1)的概率

γ的求和表示中间状态 i 可以喷射出多少种
ε的求和表示中间状态 i 喷射后有多少回喷射到 j 上

最后的π,a,b的最大似然估计就是π,A,B
HMM应用:词性标注

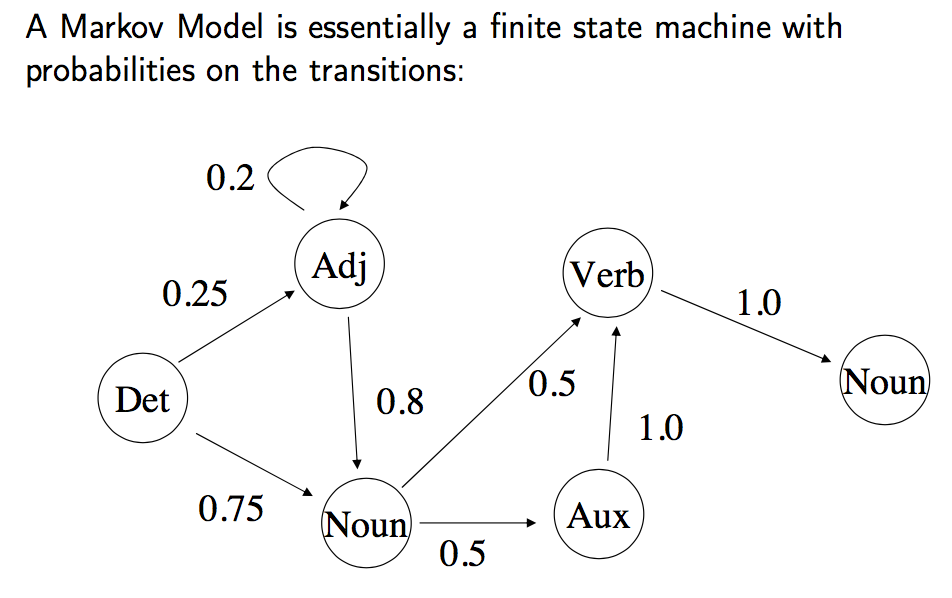




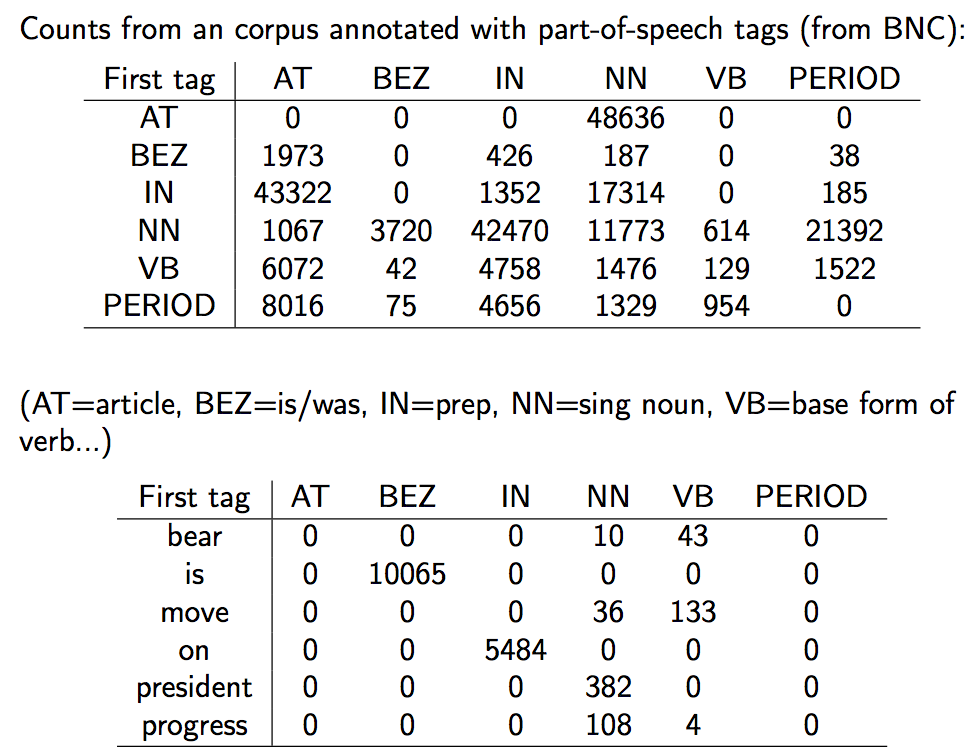
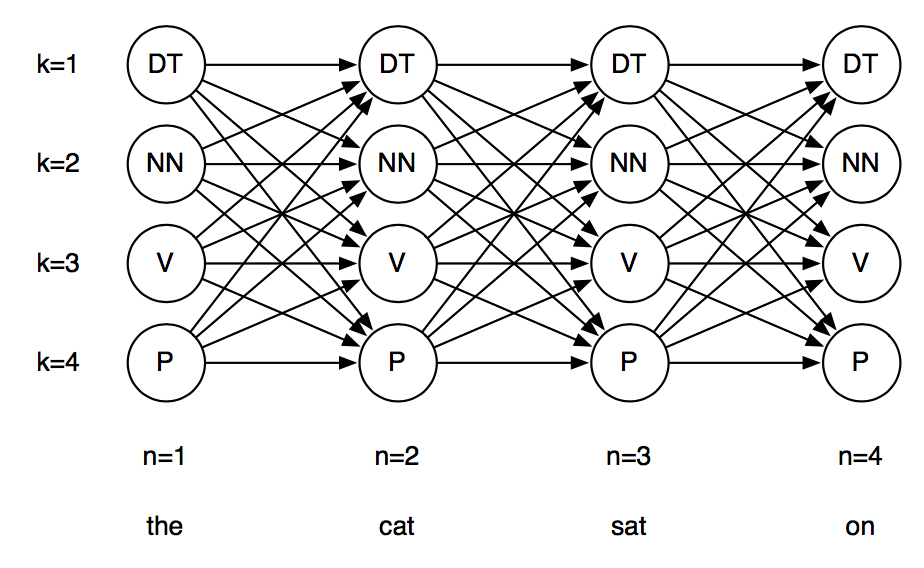


使用HMM进行词性标注
原理上课讲了。不多说。
这里我们用NLTK自带的Brown词库进行学习。
算了,稍微说几句吧。
假设我们的单词集: words = w1 ... wN
Tag集: tags = t1 ... tN
并且上课我们讲了,
P(tags | words) 正比于 P(ti | t{i-1}) * P(wi | ti)
为了找一个句子的tag,
我们其实就是找的最好的一套tags,让他最能够符合给定的单词(words)。
首先,
导入需要的库
import nltk import sys from nltk.corpus import brown
预处理词库
这里需要做的预处理是:给词们加上开始和结束符号。
Brown里面的句子都是自己标注好了的,长这个样子:(I , NOUN), (LOVE, VERB), (YOU, NOUN)
那么,我们的开始符号也得跟他的格式符合,
我们用:
(START, START) (END, END)
来代表
预处理词库 这里需要做的预处理是:给词们加上开始和结束符号。 Brown里面的句子都是自己标注好了的,长这个样子:(I , NOUN), (LOVE, VERB), (YOU, NOUN) 那么,我们的开始符号也得跟他的格式符合, 我们用: (START, START) (END, END) 来代表
词统计
这个时候,我们要把我们所有的词库中拥有的单词与tag之间的关系,做个简单粗暴的统计。
也就是我们之前说过的:
P(wi | ti) = count(wi, ti) / count(ti)
你可以自己一个个的loop全部的corpus,
当然,这里NLTK给了我们做统计的工具,(这属于没有什么必要的hack,装起逼来也不X,所以,大家想自己实现,可以去实现,不想的话,就用这里提供的方法)
# conditional frequency distribution cfd_tagwords = nltk.ConditionalFreqDist(brown_tags_words) # conditional probability distribution cpd_tagwords = nltk.ConditionalProbDist(cfd_tagwords, nltk.MLEProbDist)
好,现在我们看看平面统计下来的结果:
print("The probability of an adjective (JJ) being 'new' is", cpd_tagwords["JJ"].prob("new"))
print("The probability of a verb (VB) being 'duck' is", cpd_tagwords["VB"].prob("duck"))
好,接下来,按照课上讲的,还有第二个公式需要计算:
P(ti | t{i-1}) = count(t{i-1}, ti) / count(t{i-1})
这个公式跟words没有什么卵关系。它是属于隐层的马科夫链。
所以 我们先取出所有的tag来。
brown_tags = [tag for (tag, word) in brown_tags_words ]
# count(t{i-1} ti)
# bigram的意思是 前后两个一组,联在一起
cfd_tags= nltk.ConditionalFreqDist(nltk.bigrams(brown_tags))
# P(ti | t{i-1})
cpd_tags = nltk.ConditionalProbDist(cfd_tags, nltk.MLEProbDist)
好的,可以看看效果了:
一些有趣的结果:
那么,比如, 一句话,"I want to race", 一套tag,"PP VB TO VB"
他们之间的匹配度有多高呢?
其实就是:
P(START) * P(PP|START) * P(I | PP) * P(VB | PP) * P(want | VB) * P(TO | VB) * P(to | TO) * P(VB | TO) * P(race | VB) * P(END | VB)
prob_tagsequence = cpd_tags["START"].prob("PP") * cpd_tagwords["PP"].prob("I") * \
cpd_tags["PP"].prob("VB") * cpd_tagwords["VB"].prob("want") * \
cpd_tags["VB"].prob("TO") * cpd_tagwords["TO"].prob("to") * \
cpd_tags["TO"].prob("VB") * cpd_tagwords["VB"].prob("race") * \
cpd_tags["VB"].prob("END")
print( "The probability of the tag sequence 'START PP VB TO VB END' for 'I want to race' is:", prob_tagsequence)
Viterbi 的实现
如果我们手上有一句话,怎么知道最符合的tag是哪组呢?
首先,我们拿出所有独特的tags(也就是tags的全集)
distinct_tags = set(brown_tags)
然后 随手找句话
sentence = ["I", "want", "to", "race" ] sentlen = len(sentence)
接下来,开始维特比:
从1循环到句子的总长N,记为i
每次都找出以tag X为最终节点,长度为i的tag链
viterbi = [ ]
同时,还需要一个回溯器:
从1循环到句子的总长N,记为i
把所有tag X 前一个Tag记下来。
backpointer = [ ]
first_viterbi = { }
first_backpointer = { }
for tag in distinct_tags:
# don't record anything for the START tag
if tag == "START": continue
first_viterbi[ tag ] = cpd_tags["START"].prob(tag) * cpd_tagwords[tag].prob( sentence[0] )
first_backpointer[ tag ] = "START"
print(first_viterbi)
print(first_backpointer)
以上,是所有的第一个viterbi 和第一个回溯点。
接下来,把楼上这些,存到Vitterbi和Backpointer两个变量里去
viterbi.append(first_viterbi) backpointer.append(first_backpointer)
我们可以先看一眼,目前最好的tag是啥:
currbest = max(first_viterbi.keys(), key = lambda tag: first_viterbi[ tag ]) print( "Word", "'" + sentence[0] + "'", "current best two-tag sequence:", first_backpointer[ currbest], currbest)
好的
一些都清晰了
我们开始loop:
for wordindex in range(1, len(sentence)):
this_viterbi = { }
this_backpointer = { }
prev_viterbi = viterbi[-1]
for tag in distinct_tags:
# START没有卵用的,我们要忽略
if tag == "START": continue
# 如果现在这个tag是X,现在的单词是w,
# 我们想找前一个tag Y,并且让最好的tag sequence以Y X结尾。
# 也就是说
# Y要能最大化:
# prev_viterbi[ Y ] * P(X | Y) * P( w | X)
best_previous = max(prev_viterbi.keys(),
key = lambda prevtag: \
prev_viterbi[ prevtag ] * cpd_tags[prevtag].prob(tag) * cpd_tagwords[tag].prob(sentence[wordindex]))
this_viterbi[ tag ] = prev_viterbi[ best_previous] * \
cpd_tags[ best_previous ].prob(tag) * cpd_tagwords[ tag].prob(sentence[wordindex])
this_backpointer[ tag ] = best_previous
# 每次找完Y 我们把目前最好的 存一下
currbest = max(this_viterbi.keys(), key = lambda tag: this_viterbi[ tag ])
print( "Word", "'" + sentence[ wordindex] + "'", "current best two-tag sequence:", this_backpointer[ currbest], currbest)
# 完结
# 全部存下来
viterbi.append(this_viterbi)
backpointer.append(this_backpointer)
Word 'want' current best two-tag sequence: PP VB Word 'to' current best two-tag sequence: VB TO Word 'race' current best two-tag sequence: IN NN
找END,结束:
# 找所有以END结尾的tag sequence
prev_viterbi = viterbi[-1]
best_previous = max(prev_viterbi.keys(),
key = lambda prevtag: prev_viterbi[ prevtag ] * cpd_tags[prevtag].prob("END"))
prob_tagsequence = prev_viterbi[ best_previous ] * cpd_tags[ best_previous].prob("END")
# 我们这会儿是倒着存的。。。。因为。。好的在后面
best_tagsequence = [ "END", best_previous ]
# 同理 这里也有倒过来
backpointer.reverse()
最终:
回溯所有的回溯点
此时,最好的tag就是backpointer里面的current best
current_best_tag = best_previous
for bp in backpointer:
best_tagsequence.append(bp[current_best_tag])
current_best_tag = bp[current_best_tag]
显示结果:
best_tagsequence.reverse()
print( "The sentence was:", end = " ")
for w in sentence: print( w, end = " ")
print("\n")
print( "The best tag sequence is:", end = " ")
for t in best_tagsequence: print (t, end = " ")
print("\n")
print( "The probability of the best tag sequence is:", prob_tagsequence)
结果不是很好,说明要加更多的语料



 浙公网安备 33010602011771号
浙公网安备 33010602011771号