003-LDA

主题模型

主题模型理理论
　　直观版
　　标准版
　　公式版
实战
　　一眼看穿『希拉⾥里里邮件门』

 

什么是主体模型？

 

理论解释

理理解整个过程，涉及到⽐比较复杂数学推导。
一般来说，从公式1⼀一直推导到公式100，
大部分同学会在公式10左右的时候，就关了了直播，洗洗睡了了
所以，我今天⽤用3个不不同版本的讲解，从简单到复杂，
来让⼤大家⼀一步步理理解主体模型。
据我推测，⼤大部分⼈人是可以撑过前两个版本的。
这样，就算第三个版本太过枯燥，你也可以安⼼心的洗洗睡，⽆无妨。
么么

 

 

直观版

假设某企业想要招聘⼀一个⼯工程师，
他们收到了了⼀一把的简历，
他们想直接通过简历来看谁是⼤大⽜牛，谁是彩笔

 

简历里里通常会包含这些个人特征：

这三个要素，构成了了这家企业的⼈人⼒力力总监判断的基础：

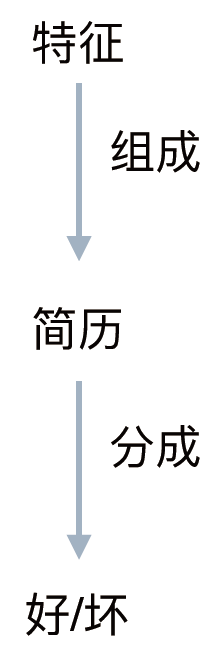
这位人力总监要做的事是：

拿出一份简历
记录下每份简历包含的特征
然而，他并不不知道，这一切代表着什什么
于是他开始猜
拿起一份简历A，
他看到里面说A参加过七⽉月课程
他就猜这位童鞋的⽔水平应该很高，八成应该是个好工程师
但是他又看到A的学历只是小学毕业，心里又有了了两成的担忧
他又看到B
又看到C
等等。。。

 

 

当然，这个猜，只是猜，没有任何证据可以证实。
但是这位人力总监是久经职场的老司机，他通过经验统计来调整自己的猜想：
- 选一份『张三』的简历，选一个特征『条纹衬衫』
- 为什什么『张三』有可能喜欢穿『条纹衬衫』？也许是因为穿条纹衬衫是优秀
程序员的信仰
- 也就是说，越多的优秀程序员穿『条纹衬衫』，越让人力总监猜想『张三』
的其他个特征也符合优秀程序员的喜好，并且『张三』本人穿『条纹衬衫』
是一个优秀的程序员自我修养的体现
- 继续猜，继续拿『张三』和『条纹衬衫』两个元素。人力总监转念一想，也
有可能爱穿条纹的都是彩笔。
- 于是他按照上面的逻辑，再看看『张三』穿『条纹衬衫』是『彩笔』的可能
性有多少
- 把所有的简历和所有的特征都做个组合，都来猜一下是彩笔还是大牛

 

久经沙场之后，老司机人力总监掌握了了如下信息：
对于是不是优秀程序员的分类，它通过人头统计大概有了了数
这让他在以后看到新简历的时候，一眼就知道他是不是个优秀程序员
对于每个特征C，他也能说出大概百分之多少的人拥有特征C可以说明他们是优秀的程序员。

 

 

 总结成公式就是：

以上，就是我们用现实的例子模拟的LDA模型来区分简历好坏在文本的主题分类中，我们的例子和实际之间的联系如下：

 

 

 

 

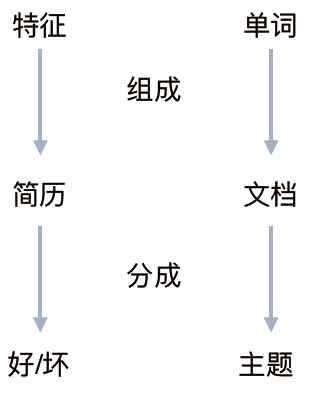
 什么是LDA？

Latent Dirichlet Allocation:
是一种无监督的贝叶斯模型
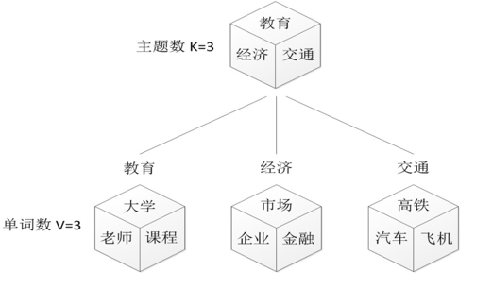
是一种主题模型，它可以将文档集中每篇文档的主题按照概率分布的形式给出。同时它是一种无监督学习算法，在训练时不需要手工标注的训练集，需要的仅仅是文档集以及指定主题的数量量k即可。此外LDA的另一个优点则是，对于每一个主题均可找出一些词语来描述它。
是一种典型的词袋模型，即它认为一篇文档是由一组词构成的一个集合，词与词之间没有顺序以及先后的关系。一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。
— wikipedia

 

 什么是贝叶斯模型？

理论

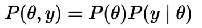
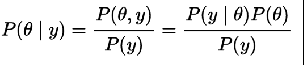
模型

- 用概率作为『可信度』
- 每次看到新数据，就更更新『可信度』
- 需要一个模型来解释数据的生成

 

 

 先验，后验与似然

 

 

 

 

 

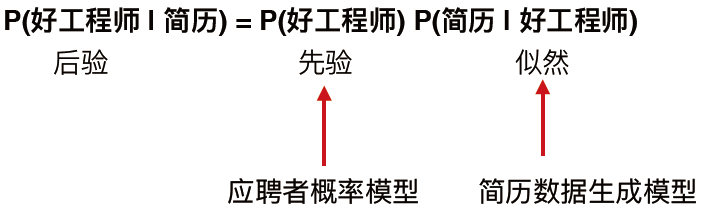
标准版

 我们用LDA找寻的就是之前例子里总监大人统计出来的经验：

一份简历的每个特征都是因为本人有一定概率是好/坏程序员，并从好/坏这个分类中以一定概率选择某些特征而组成的

一篇文章的每个词都是以一定概率选择了某个主题，并从这个主题中以一定概率选择某个词语而组成的

P(单词 | 文档) = P(单词 | 主题) * P(主题 | 文档)

 

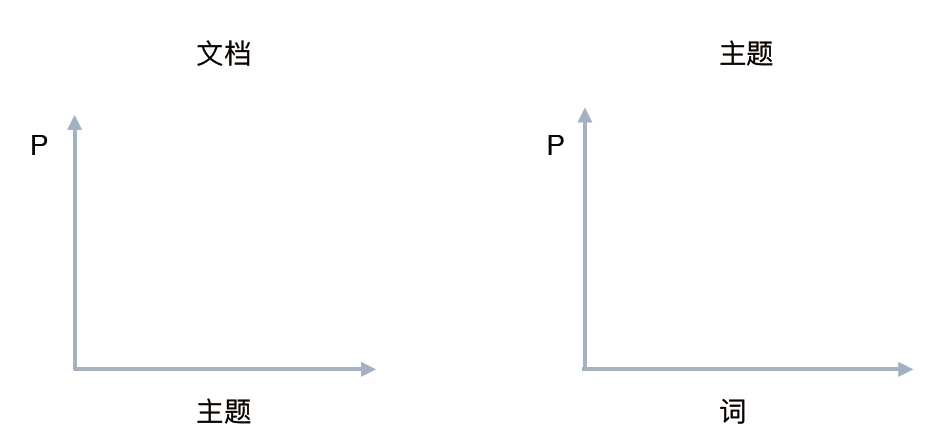
LDA生成过程

对于语料料库中的每篇文档，LDA定义了如下生成过程（generative process）：
1.对每一篇文档，从主题分布中抽取一个主题；
2.从上述被抽到的主题所对应的单词分布中抽取一个单词；
3.重复上述过程直至遍历文档中的每一个单词。

 

 

稍微具体点儿讲：
（w代表单词；d代表⽂文档；t代表主题；⼤大写代表总集合，⼩小写代表个体。）
标准版
D中每个文档d看作⼀一个单词序列列<w1,w2,...,wn>，wi表示第i个单词。
D中涉及的所有不同单词组成一个词汇表大集合V (vocabulary)，LDA以文档集合D
作为输入，希望训练出的两个结果向量量（假设形成k个topic，V中⼀一共m个词）：
 对每个D中的文档d，对应到不不同Topic的概率θd<pt1,...,ptk>，其中，pti表示d对应T中第i个topic的概率。计算方法是直观的，pti=nti/n，其中nti表示d中对应第i个topic的词的数目，n是d中所有词的总数。
 对每个T中的topict，生成不不同单词的概率φt<pw1,...,pwm>，其中，pwi表示t生成V中第i个单词的概率。计算方法同样很直观，pwi=Nwi/N，其中Nwi表示对应到topict的V中第i个单词的数目，N表示所有对应到topict的单词总数。

 用人话说：

pti=某个词在某个主题中的数目/某个词在某个文档中的数目

pwi=某个词在某个主题中的数量/某个词在所有文档中的数量

 

 

所以，LDA的核心公式如下：
P(w|d)=P(w|t)*P(t|d)
直观的看这个公式，就是以Topic作为中间层，可以通过当前的θd和φt给出了文档d中出现单词w的概率。其中p(t|d)利用θd计算得到，p(w|t)利用φt计算得到。
实际上，利用当前的θd和φt，我们可以为一个文档中的一个单词计算它对应任意一个Topic时的p(w|d)，然后根据这些结果来更新这个词应该对应的topic。然后，如果这个更新改变了了这个单词所对应的Topic，就会反过来影响θd和φt

 

 LDA学习过程

LDA算法开始时，先随机地给θd和φt赋值（对所有的d和t）。然后：

1.针对一个特定的文档ds中的第i单词wi，如果令该单词对应的topic为tj，可以把上述公式改写为：Pj(wi | ds)=P(wi | tj)*P(tj | ds) = φt*θd

2.现在我们可以举T中的topic，得到所有的pj(wi | ds)。然后可以根据这些概率值结果为ds中的第i个单词wi选择一个topic。最简单的想法是取令pj(wi | ds)最大的tj（注意，这个式子里只有j是变量量）

3.然后，如果ds中的第i个单词wi在这里选择了一个与原先不同的topic（也就是说，这个时候i在遍历ds中所有的单词，而tj理当不变），就会对θd和φt有影响了了。它们的影响又会反过来影响对上面提到的p(w | d)的计算。对D中所有的d中的所有w进行一次p(w | d)的计算并重新选择topic看作一次迭代。这样进行n次循环迭代之后，就会收敛到LDA所需要的结果了。

用人话说：

P(单词|文档)=P(单词|主题)*P(主题|文档)

最终要求的是：P(主题|文档)

已知的是：P(单词|文档)

1，一个文档中，某个词对应一个主题。

2，选择所有主题中的每一个主题进行计算，得到所有的P(单词|文档)，然后根据这个概率，为这个词选择一个主题。

3，第二步为这个词选择的主题，不是原先的主题，那么就更新P(单词|主题)，P(主题|文档)，更新他两的同时也会根据公式得到新的P(单词|文档)，知道更新的P(单词|文档)与已知的P(单词|文档)相同，那么P(单词|主题)和P(主题|文档)就可以确定下来

要求的不就是P(主题|文档)么。

搞不懂这些培训机构为什么不说人话！！！

 

 

 公式版：

现在，我们对LDA的玩法基本了了解了了，
我们终于可以安静的刷刷公式了了（注：尿点时刻）：
这一部分的解释，可以参照七月在线创始人July的CSDN博客：
http://blog.csdn.net/v_july_v/article/details/41209515

 

 

正经的理理解LDA，分为下述5个步骤：

一个函数：gamma函数
四个分布：二项分布、多项分布、beta分布、Dirichlet分布
一个概念和一个理理念：共轭先验和贝叶斯框架
两个模型：pLSA、LDA
一个采样：Gibbs采样

 

共轭分布与共轭先验：

 

 

 

Gamma函数
阶乘函数在实数上的推广。
我们知道，对于整数⽽而言：

 

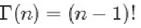
对于实数：

 

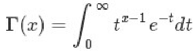
二项分布（Binomial distribution）

二项分布是从伯努利利分布推进的。伯努利利分布，又称两点分布或0-1分布，是一个离散型的随机分布，其中的随机变量量只有两类取值，非正即负{+，-}。而二项分布即重复n次的伯努利利试验，记为 。简言之，只做一次实验，是伯努利利分布，重复做了了n次，是二项分布。二项分布的概率密度
函数为：

 

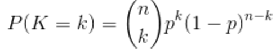
多项分布，是二项分布扩展到多维的情况

多项分布是指单次试验中的随机变量量的取值不不再是0-1的，而是有多种离散值可能（1,2,3...,k）。比如投掷6个⾯面的骰子实验，N次实验结果服从K=6的多项分布。当然啦，他们加起来的P应该是等于1的。
多项分布的概率密度函数为：

 

 

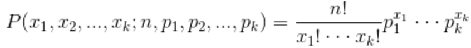
Beta分布，二项分布的共轭先验分布
给定参数a>0和b>0，取值范围为[0,1]的随机变量量 x 的概率密度函数：

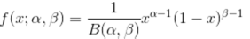
其中：

 

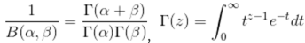
 Dirichlet分布，是beta分布在高维度上的推⼴广

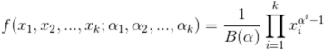
其中

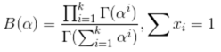
贝叶斯派的思考方式：

几个主题模型（循序渐进）：

Unigram model

 

 

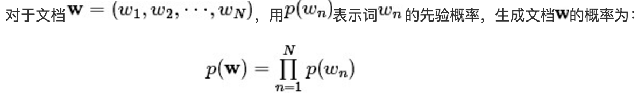
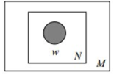
Mixture of unigrams model

该模型的生成过程是：给某个文档先选择一个主题z，再根据该主题生成文档，该文档中的所有词都来自一个主题。假设主题有z1,z2,z3,...zk，生成文档的概率为：

 

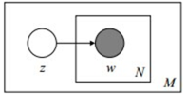
 PLSA模型

刚刚的mix unigram模型里里面，一篇文章只给了了一个主题。但是现实生活中，一篇文章可能有多个主题，只不不过是『出现的⼏几率』不一样。

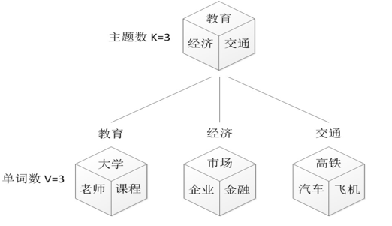
我们定义：

我们的文本生成模型就是：
（还记得什什么是文本生成模型嘛？返回标准版part回顾一下）

我们通过观测，得到了『知道主题是什么，我就用什么单词』的文本生成模型，那么，根据贝叶斯定律律，我们就可以反过来推出『看见用了了什么单词，我就知道主题是什么』

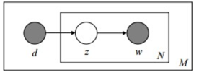
LDA模型

LDA就是在pLSA的基础上加层⻉贝叶斯框架，即LDA就是pLSA的⻉贝叶斯版本

 

PLSA与LDA对比

PLSA

LDA

pLSA跟LDA的本质区别就在于它们去估计未知参数所采用的思想不不同，前者⽤用的是频率派思想，后者用的是贝叶斯派思想。

 

 

 

 

 

LDA模型应用：一眼看穿希拉里的邮件

我们拿到希拉里泄露的邮件，跑一把LDA，看看她平时都在聊什么。

首先，导入我们需要的一些库

 

import numpy as np
import pandas as pd
import re

　　

然后，把希婆的邮件读取进来。

这里我们用pandas。不熟悉pandas的朋友，可以用python标准库csv

df = pd.read_csv("../input/HillaryEmails.csv")
# 原邮件数据中有很多Nan的值，直接扔了。
df = df[['Id','ExtractedBodyText']].dropna()

　　

文本预处理：

上过我其他NLP课程的同学都知道，文本预处理这个东西，对NLP是很重要的。

我们这里，针对邮件内容，写一组正则表达式：

（不熟悉正则表达式的同学，直接百度关键词，可以看到一大张Regex规则表）

 

def clean_email_text(text):
    text = text.replace('\n'," ") #新行，我们是不需要的
    text = re.sub(r"-", " ", text) #把 "-" 的两个单词，分开。（比如：july-edu ==> july edu）
    text = re.sub(r"\d+/\d+/\d+", "", text) #日期，对主体模型没什么意义
    text = re.sub(r"[0-2]?[0-9]:[0-6][0-9]", "", text) #时间，没意义
    text = re.sub(r"[\w]+@[\.\w]+", "", text) #邮件地址，没意义
    text = re.sub(r"/[a-zA-Z]*[:\//\]*[A-Za-z0-9\-_]+\.+[A-Za-z0-9\.\/%&=\?\-_]+/i", "", text) #网址，没意义
    pure_text = ''
    # 以防还有其他特殊字符（数字）等等，我们直接把他们loop一遍，过滤掉
    for letter in text:
        # 只留下字母和空格
        if letter.isalpha() or letter==' ':
            pure_text += letter
    # 再把那些去除特殊字符后落单的单词，直接排除。
    # 我们就只剩下有意义的单词了。
    text = ' '.join(word for word in pure_text.split() if len(word)>1)
    return text

好的，现在我们新建一个colum，并把我们的方法跑一遍：

docs = df['ExtractedBodyText']
docs = docs.apply(lambda s: clean_email_text(s))  

好，来看看长相：

docs.head(1).values

array([ 'Thursday March PM Latest How Syria is aiding Qaddafi and more Sid hrc memo syria aiding libya docx hrc memo syria aiding libya docx March For Hillary'], dtype=object)

我们直接把所有的邮件内容拿出来。

doclist = docs.values

　　

LDA模型构建：

好，我们用Gensim来做一次模型构建

首先，我们得把我们刚刚整出来的一大波文本数据

[[一条邮件字符串]，[另一条邮件字符串], ...]

转化成Gensim认可的语料库形式：

[[一，条，邮件，在，这里],[第，二，条，邮件，在，这里],[今天，天气，肿么，样],...]

引入库：

 

from gensim import corpora, models, similarities
import gensim

　　

为了免去讲解安装NLTK等等的麻烦，我这里直接手写一下停止词列表：

这些词在不同语境中指代意义完全不同，但是在不同主题中的出现概率是几乎一致的。所以要去除，否则对模型的准确性有影响

 

stoplist = ['very', 'ourselves', 'am', 'doesn', 'through', 'me', 'against', 'up', 'just', 'her', 'ours', 
            'couldn', 'because', 'is', 'isn', 'it', 'only', 'in', 'such', 'too', 'mustn', 'under', 'their', 
            'if', 'to', 'my', 'himself', 'after', 'why', 'while', 'can', 'each', 'itself', 'his', 'all', 'once', 
            'herself', 'more', 'our', 'they', 'hasn', 'on', 'ma', 'them', 'its', 'where', 'did', 'll', 'you', 
            'didn', 'nor', 'as', 'now', 'before', 'those', 'yours', 'from', 'who', 'was', 'm', 'been', 'will', 
            'into', 'same', 'how', 'some', 'of', 'out', 'with', 's', 'being', 't', 'mightn', 'she', 'again', 'be', 
            'by', 'shan', 'have', 'yourselves', 'needn', 'and', 'are', 'o', 'these', 'further', 'most', 'yourself', 
            'having', 'aren', 'here', 'he', 'were', 'but', 'this', 'myself', 'own', 'we', 'so', 'i', 'does', 'both', 
            'when', 'between', 'd', 'had', 'the', 'y', 'has', 'down', 'off', 'than', 'haven', 'whom', 'wouldn', 
            'should', 've', 'over', 'themselves', 'few', 'then', 'hadn', 'what', 'until', 'won', 'no', 'about', 
            'any', 'that', 'for', 'shouldn', 'don', 'do', 'there', 'doing', 'an', 'or', 'ain', 'hers', 'wasn', 
            'weren', 'above', 'a', 'at', 'your', 'theirs', 'below', 'other', 'not', 're', 'him', 'during', 'which']

　　

人工分词：

这里，英文的分词，直接就是对着空白处分割就可以了。

中文的分词稍微复杂点儿，具体可以百度：CoreNLP, HaNLP, 结巴分词，等等

分词的意义在于，把我们的长长的字符串原文本，转化成有意义的小元素：

texts = [[word for word in doc.lower().split() if word not in stoplist] for doc in doclist]

　　这时候，我们的texts就是我们需要的样子了：

texts[0]

　　

['thursday',
 'march',
 'pm',
 'latest',
 'syria',
 'aiding',
 'qaddafi',
 'sid',
 'hrc',
 'memo',
 'syria',
 'aiding',
 'libya',
 'docx',
 'hrc',
 'memo',
 'syria',
 'aiding',
 'libya',
 'docx',
 'march',
 'hillary']

 

建立语料库

用词袋的方法，把每个单词用一个数字index指代，并把我们的原文本变成一条长长的数组：

dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]

　　给你们看一眼：

corpus[13]

　　

[(36, 1), (505, 1), (506, 1), (507, 1), (508, 1)]

 

这个列表告诉我们，第14（从0开始是第一）个邮件中，一共6个有意义的单词（经过我们的文本预处理，并去除了停止词后）

其中，36号单词出现1次，505号单词出现1次，以此类推。。。

接着，我们终于可以建立模型了：

 

lda = gensim.models.ldamodel.LdaModel(corpus=corpus, id2word=dictionary, num_topics=20)

　　我们可以看到，第10号分类，其中最常出现的单词是：

lda.print_topic(10, topn=5)

'0.007*kurdistan + 0.006*email + 0.006*see + 0.005*us + 0.005*right'
我们把所有的主题打印出来看看

lda.print_topics(num_topics=20, num_words=5)

　　

[(0, '0.010*nuclear + 0.006*us + 0.005*american + 0.005*iran + 0.005*also'),
 (1,
  '0.019*labour + 0.016*dialogue + 0.015*doc + 0.015*strategic + 0.014*press'),
 (2, '0.007*mr + 0.007*us + 0.006*would + 0.006*new + 0.004*israel'),
 (3,
  '0.013*israel + 0.011*israeli + 0.011*settlements + 0.007*settlement + 0.006*one'),
 (4, '0.012*us + 0.007*diplomacy + 0.006*state + 0.005*know + 0.005*would'),
 (5, '0.045*call + 0.021*yes + 0.020*thx + 0.010*ops + 0.009*also'),
 (6,
  '0.012*obama + 0.009*percent + 0.008*republican + 0.007*republicans + 0.006*president'),
 (7,
  '0.069*pm + 0.036*office + 0.027*secretarys + 0.021*meeting + 0.020*room'),
 (8, '0.008*would + 0.006*party + 0.006*new + 0.005*said + 0.005*us'),
 (9, '0.007*us + 0.006*would + 0.005*state + 0.005*new + 0.005*netanyahu'),
 (10, '0.007*kurdistan + 0.006*email + 0.006*see + 0.005*us + 0.005*right'),
 (11,
  '0.007*health + 0.007*haitian + 0.006*people + 0.005*would + 0.005*plan'),
 (12, '0.012*see + 0.009*like + 0.009*back + 0.008*im + 0.008*would'),
 (13, '0.009*new + 0.007*fyi + 0.006*draft + 0.006*speech + 0.005*also'),
 (14,
  '0.006*military + 0.006*afghanistan + 0.005*security + 0.005*said + 0.005*government'),
 (15, '0.033*ok + 0.028*pls + 0.023*print + 0.014*call + 0.011*pis'),
 (16,
  '0.015*state + 0.008*sounds + 0.007*us + 0.006*department + 0.005*sorry'),
 (17, '0.053*fyi + 0.012*richards + 0.006*us + 0.005*like + 0.004*defenses'),
 (18, '0.043*pm + 0.021*fw + 0.018*cheryl + 0.015*mills + 0.014*huma'),
 (19, '0.012*clips + 0.007*read + 0.006*tomorrow + 0.006*see + 0.005*send')]

 

接下来：

通过

lda.get_document_topics(bow)

或者

lda.get_term_topics(word_id)

两个方法，我们可以把新鲜的文本/单词，分类成20个主题中的一个。

但是注意，我们这里的文本和单词，都必须得经过同样步骤的文本预处理+词袋化，也就是说，变成数字表示每个单词的形式。