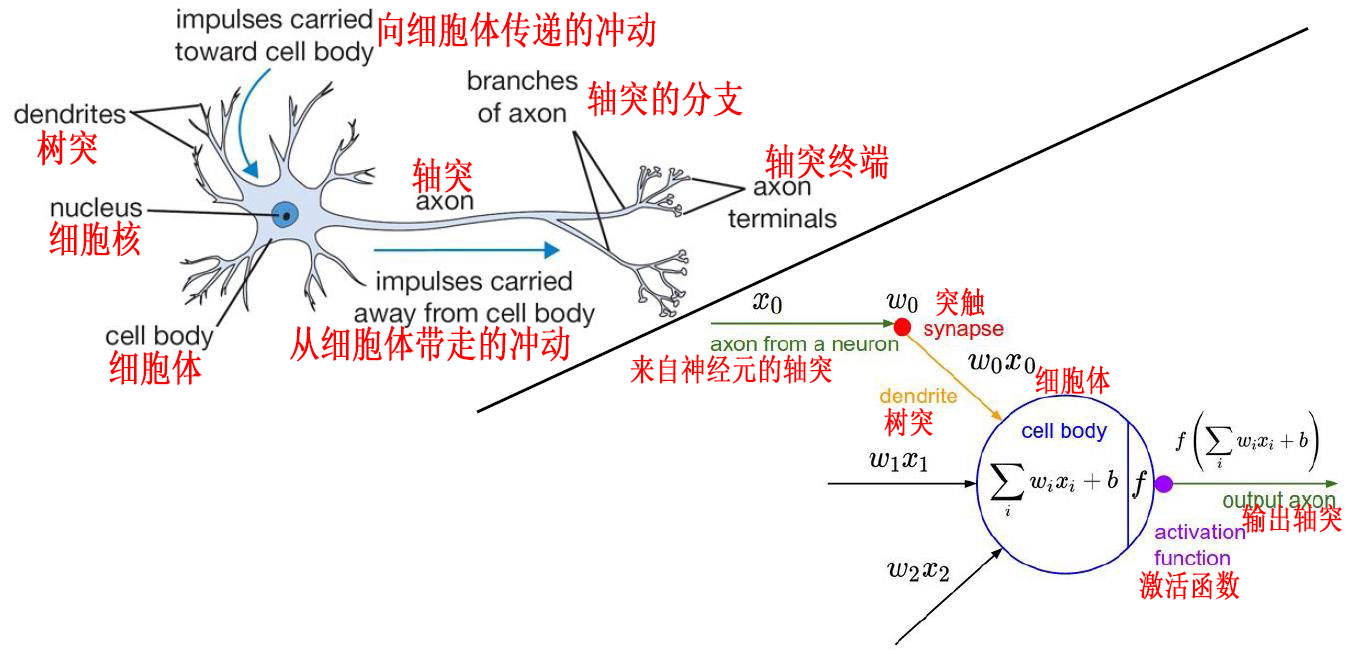
004-神经网络

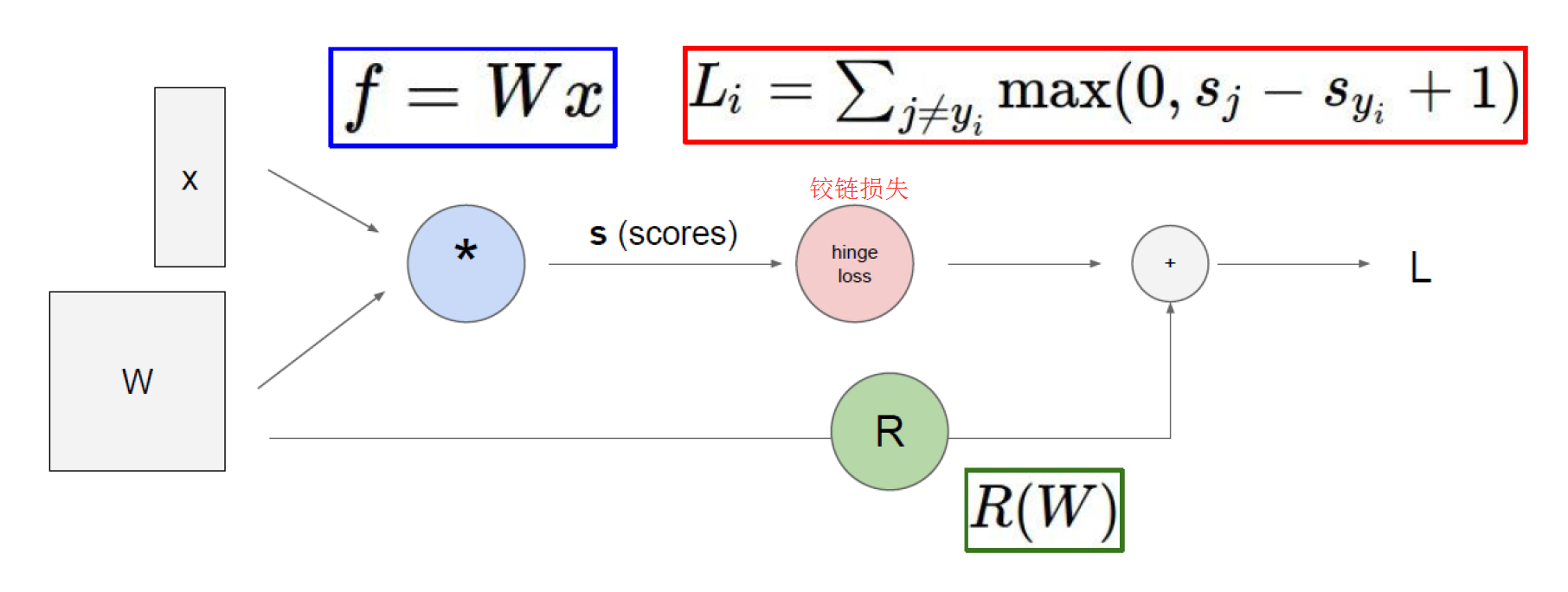
神经网络公式与模型：

 

神经网络在计算机中的样子：

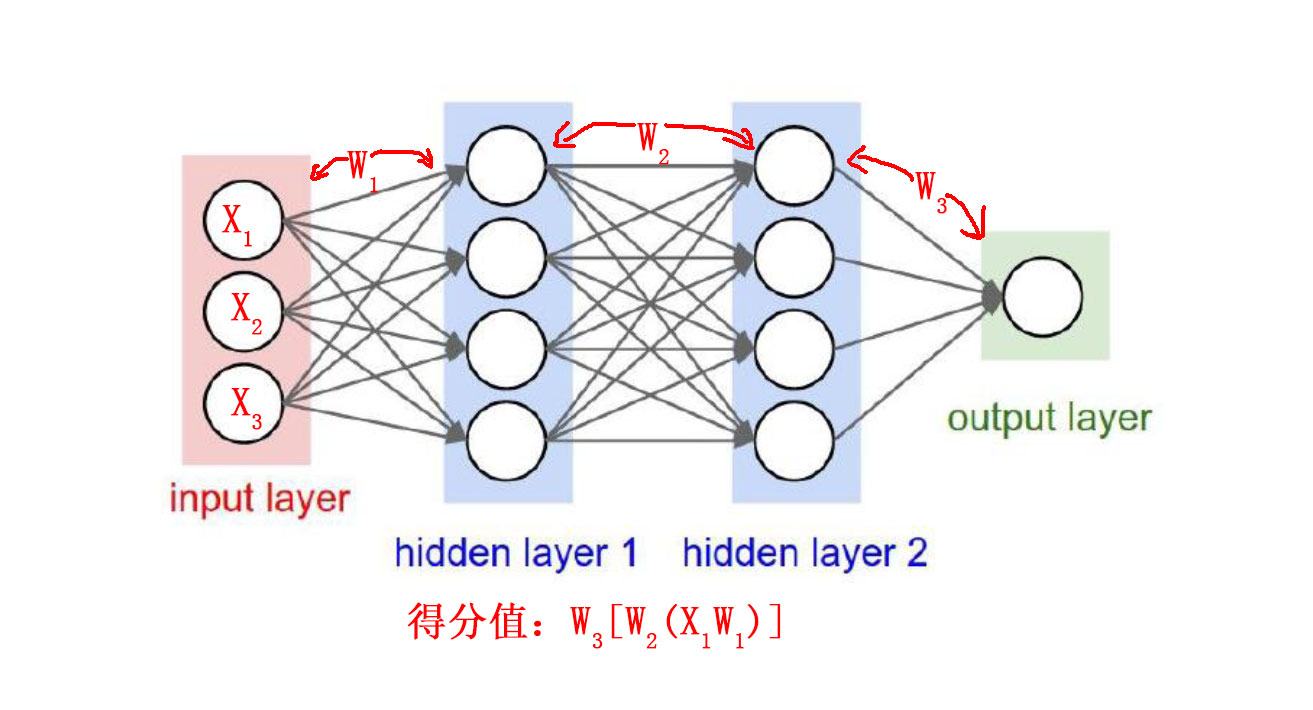
输入层和隐藏1层用w1链接，隐藏1和隐藏2层用w2链接，隐藏2层和输出层用w3链接。

那么w1应该是一个3×4的矩阵，表示有3个样本，4个特征。

 

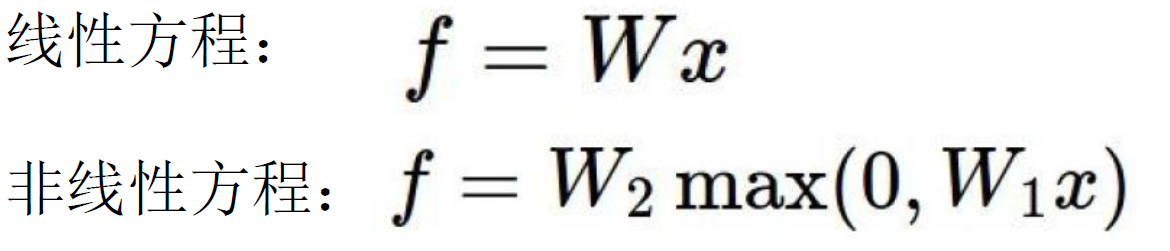
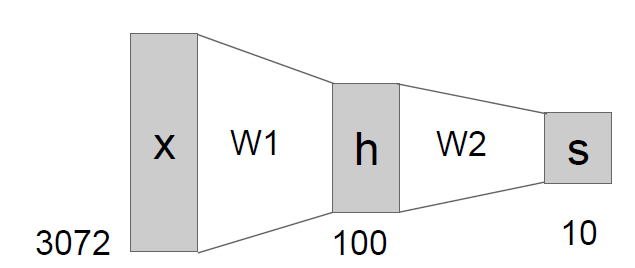
线性很少能满足实际要求，于是非线性的函数出现了，max（0，w1x）称为激活函数

例如用sigmoid当做激活函数，将任意值压缩至0~1的区间范围内。

就好比在第一个隐藏层后加一个激活函数，在第二个隐藏层后加一个激活函数。。。。。。

 

多层神经网络：

单层的神经网络：

　　

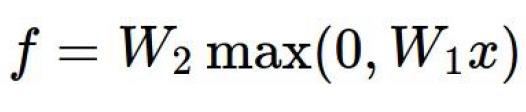
双层神经网络：

　　

 

激活函数：

在神经网络中，sigmoid函数会出现梯度消失的情况

什么叫做梯度消失的情况？说白了就是在反向传播时，要对激活函数求偏导数，如果x的值很大，那么在sigmoid函数中偏导数就会接近于0，再进行偏导数的累乘，那么就会更接近于0，这就叫做梯度消失。

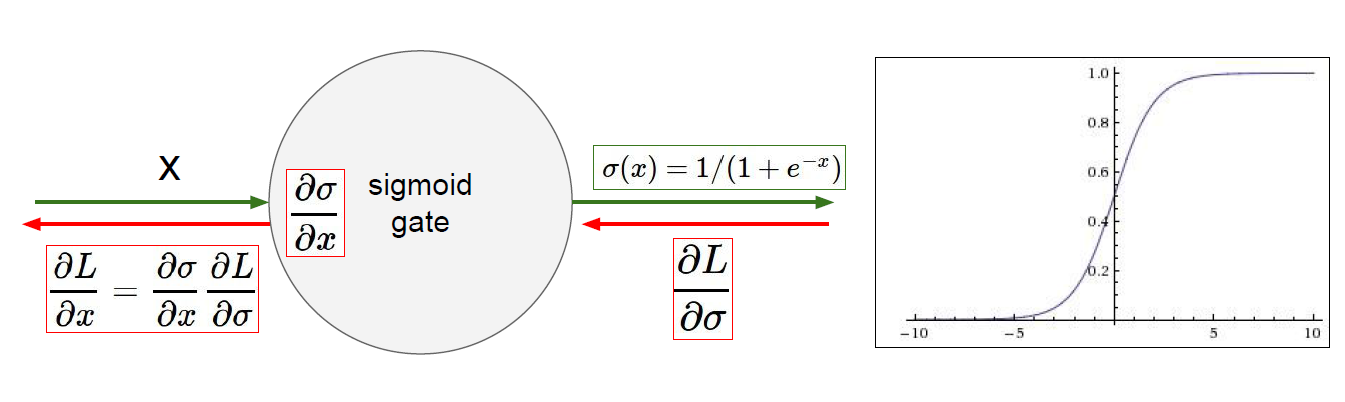
解决的方法：

通过relu函数

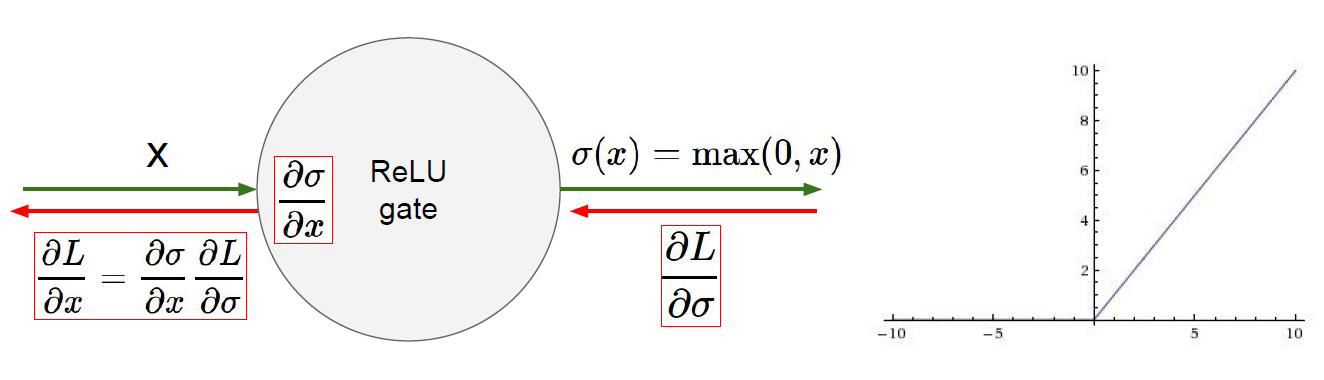
当做激活函数。

 

神经网络层数（神经元）选择：

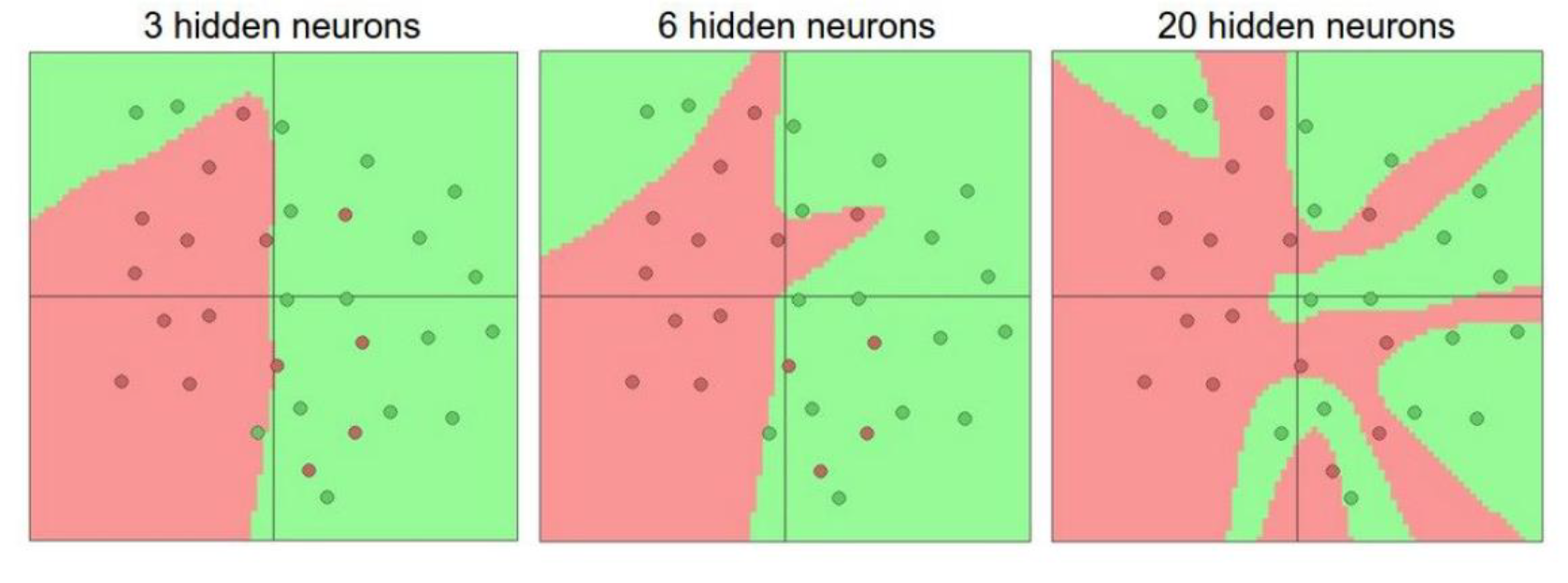
可以看到中间的隐藏层（以后叫做神经元）越多，分类的效果就越好，但是容易过拟合，这也是神经网络的最大缺点，神经元的提升泛化能力减弱，过拟合的风险提高。

 

正则化项在神经网络中的重要作用：

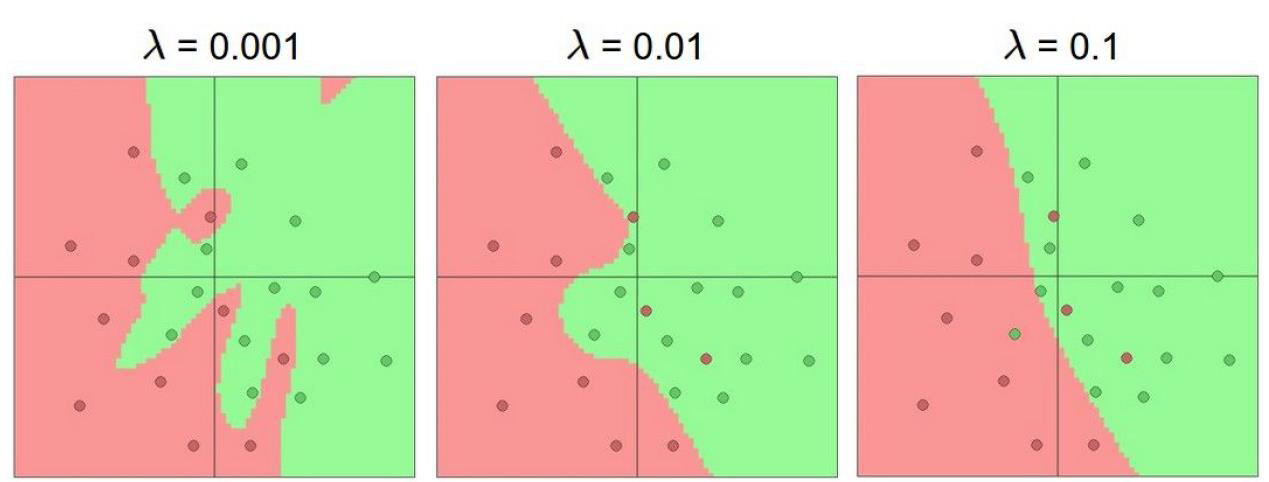
当在损失函数中添加正则化惩罚项，可以见得惩罚系数越高，过拟合的风险就越小。

 

drop-out：

左边的叫做全连接，更容易过拟合。

所以用右图来解决，就是增加迭代次数，每次迭代减少神经元的个数。

 

数据预处理：

数据的归一化操作

图一是原始数据

图二是将原始数据减去了一个均值的操作，就会以0位中心。

图三是将图二进行了除以标准差的操作，数据就会在纵轴上缩小。

 

权重初始化：

D-维数

h-神经元个数

b对最终结果影响一般很小。所以

b=0或1