DBSCAN聚类算法

基本概念：（Density-Based Spatial Clustering of Applications with Noise）基于密度的噪声应用空间聚类

核心对象：若某个点的密度达到算法设定的阈值则其为核心点。
（即r 邻域内点的数量不小于minPoints）

ϵ-邻域的距离阈值：设定的半径r

直接密度可达：若某点p在点q的r 邻域内，且q是核心点则p-q直接密度可达。

密度可达：若有一个点的序列q0、q1、…qk，对任意qi-qi-1是直接密度可达的，则称从q0到qk密度可达，这实际上是直接密度可达的“传播”。

密度相连：若从某核心点p出发，点q和点k都是密度可达的,则称点q和点k是密度相连的。

边界点:属于某一个类的非核心点,不能发展下线了

直接密度可达：若某点p在点q的r 邻域内，且q是核心点则p-q直接密度可达。

噪声点：不属于任何一个类簇的点，从任何一个核心点出发都是密度不可达的

用人话说：每个点都可以画一个圈，在圈内点的叫直接密度可达，能间接被圈上的叫做密度可达，隔了好几层被间接圈上的叫做密度相连，被圈之后，圈不到其他新的点的叫做边界点，谁也圈不到的叫做离群点（噪音点）。

一张图

 

 工作流程：

参数D：输入数据集

参数ϵ：指定半径

MinPts：密度阈值

 

 

 参数选择：

半径ϵ，可以根据K距离来设定：找突变点K距离：给定数据集P={p(i); i=0,1,…n}，计算点P(i)到集合D的子集S中所有点之间的距离，距离按照从小到大的顺序排序，d(k)就被称为k-距离。

 MinPts：密度值也就是点的数量。

 

 

优势：

不需要指定簇个数

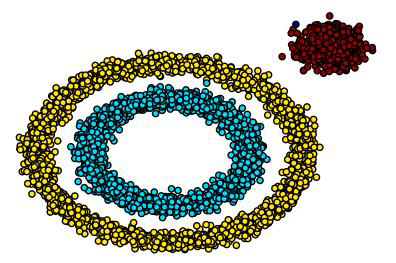
可以发现任意形状的簇

擅长找到离群点（检测任务）

两个参数就够了

 

 劣势：

高维数据有些困难（可以做降维）
Sklearn中效率很慢（数据削减策略）
参数难以选择（参数对结果的影响非常大）

 

可视化展示网站： 

https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/