001-决策树算法介绍

树模型：

决策树：从根节点一步一步走到叶子节点（决策）

所有的数据最终都会落到叶子节点，既可以做分类也可以做回归

例如：

一家5个人是否愿意玩电脑游戏：

 

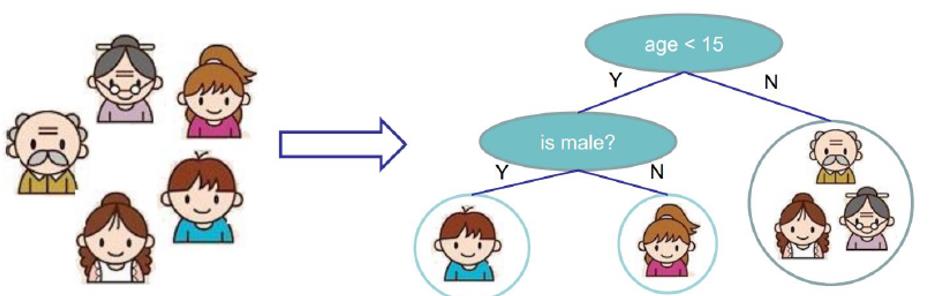
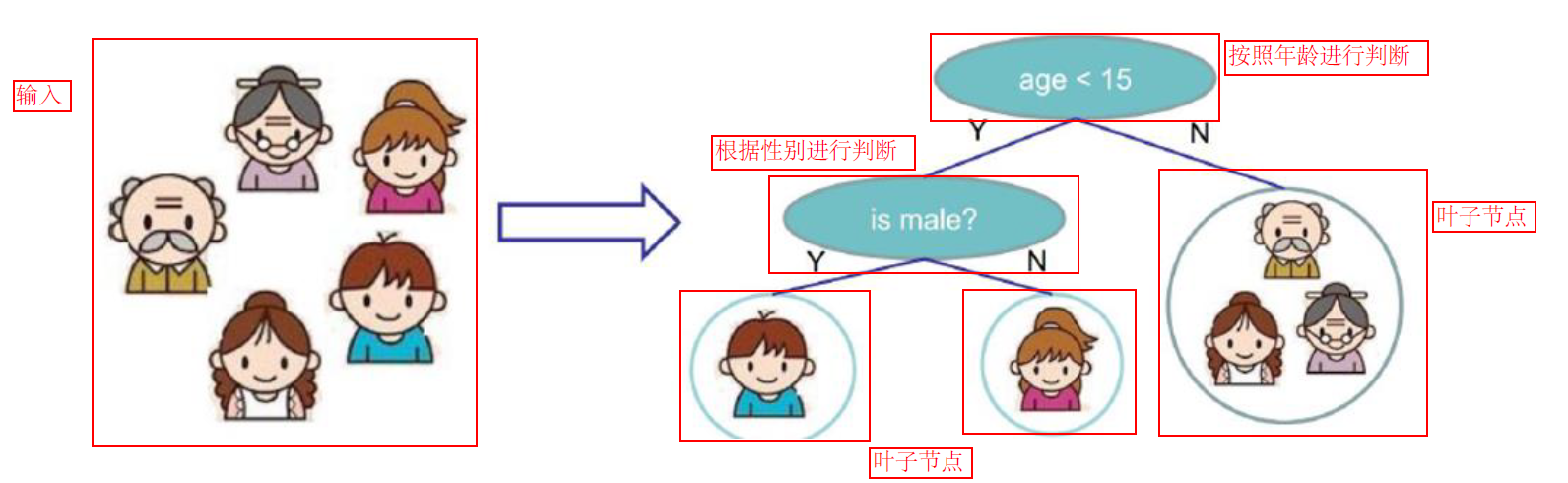
树的组成：

根节点：第一个选择点

　　　　最重要的节点，也是分类效果最明显的方式

非叶子节点与分支：中间过程

　　　　　　　　   进一步的分类，效果没有根节点明显

叶子节点：最终决策的结果

决策树就相当于是选秀节目，层层选拔

 

 

节点：

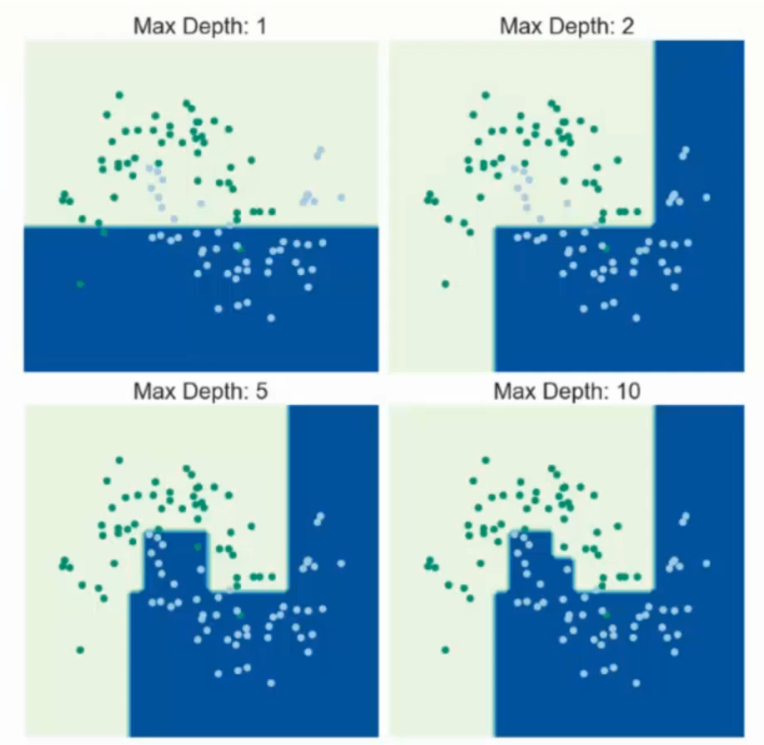
　　增加节点相当于在数据内部横切一刀

　　节点是否是越多越好？

　　　　　　　　　　　　表面看起来像是这样，实际中不是，后边会提到

　　　　　　　　　　　　

 

 

 

决策树的训练与测试：

训练阶段：从给定的训练集构造出来一棵树（从跟节点开始选择特征，如何进行特征切分）

测试阶段：根据构造出来的树模型从上到下去走一遍就好了

一旦构造好了决策树，那么分类或者预测任务就很简单了，只需要走一遍就可以了，那么难点就在于如何构造出来一颗树，这就没那么容易了，需要考虑的问题还有很多的！

 

 

 

如何切分特征（选择节点）

问题：根节点的选择该用哪个特征呢？接下来呢？如何切分呢？

想象一下：我们的目标应该是根节点就像一个老大似的能更好的切分数据（分类的效果更好），根节点下面的节点自然就是二当家了。

目标：通过一种衡量标准，来计算通过不同特征进行分支选择后的分类情况，找出来最好的那个当成根节点，以此类推。

 

那么衡量标准该如何选取呢？根据什么？例如比武是根据武力高强，唱歌是根据唱歌好坏，我不是明星是根据拼爹爹。

我们的数据衡量标准

 

 

衡量标准-熵

熵：熵是表示随机变量不确定性的度量

（解释：说白了就是物体内部的混乱程度，比如杂货市场里面什么都有那肯定混乱呀，专卖店里面只卖一个牌子的那就稳定多啦，也就是混乱程度越大的熵值越大）

$H(X)=-\sum Pi*logPi,i=1,2,3,...,n$

-求和（取到一个类别的概率*log该类别的概率）

一个栗子：A集合[1,1,1,1,1,1,1,1,2,2]
　　　　　B集合[1,2,3,4,5,6,7,8,9,1]

显然A集合的熵值要低，因为A里面只有两种类别，相对稳定一些而B中类别太多了，熵值就会大很多。（在分类任务中我们希望通过节点分支后数据类别的熵值大还是小呢？）

如果有一个C集合[1,1,1,1,1,1,1,1,1,1]，则LogPC= 0，1出现的概率是100%

 

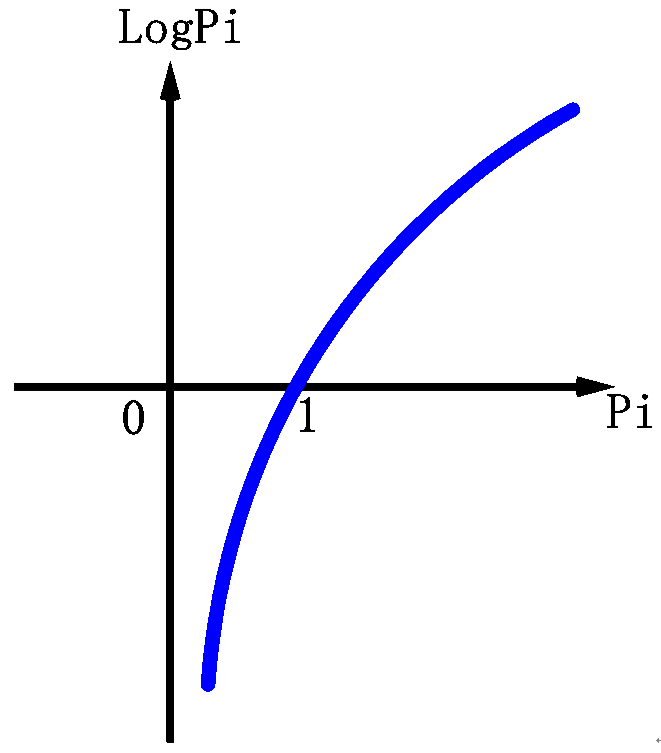
如果Pi的值很大，也就是说i的概率很大，那么LogPi的值就很接近于0，反之LogPi的值就会越小，前边有一个负号，则-LogPi的值就越大，

那么越大说明熵值越大，也就是越混乱，也就是i内的每个元素，出现概率很小，也就是权重很低，说明i内的每个元素很分散，相同程度很小，

反之，越接近于0的时候，就说明，i内的每个元素，出现概率很大，也就是权重很高，说明i内的每个元素很集中，相同程度很大。

 

熵：不确定性越大，得到的熵值也就越大

看下图：

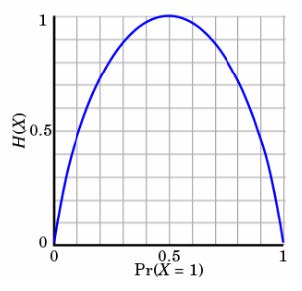
例如抛硬币：

当p=0或p=1时，H(p)=0,随机变量完全没有不确定性，0表示正面，1表示反面，或者说，0表示完全不发生，1表示100%发生
当p=0.5时，H(p)=1,此时随机变量的不确定性最大，0.5表示中间的混乱值

如何决策一个节点的选择呢？

信息增益：表示特征X使得类Y的不确定性减少的程度。（分类后的专一性，希望分类后的结果是同类在一起），也就是按照这个方法分类后，熵值变小了

增益的意思就是，原来的熵值如果是10，分类后熵值变为8，那么信息增益就是10-8=2，

也就是说，寻找信息增益最大的分类方法。

接着在寻找信息增益第二大，第三大，第四大。。。。。