003-逻辑回归

目的：分类还是回归？经典的二分类算法，其实做的是分类任务

机器学习算法选择：先逻辑回归再用复杂的，能简单还是用简单的

逻辑回归的决策边界：可以是非线性的

 

 

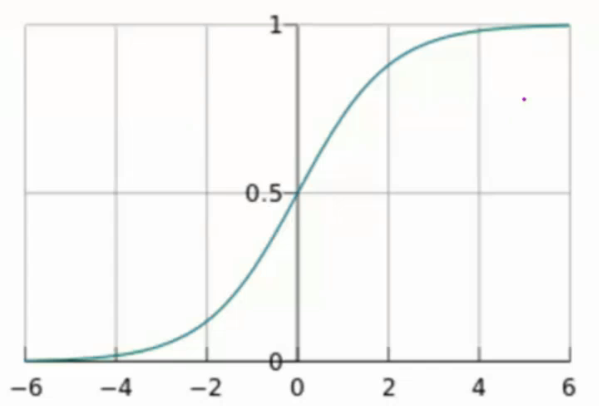
sigmoid函数

公式：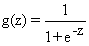

自变量为任意实数，值域为[0,1]

y的取值范围是0-1，相当于概率

此函数相当于概率论中的概率密度累积函数

输入范围是（-oo，+oo），输出范围[0,1]

将线性回归预测出的一个值，放到sigmoid函数当中来，转换为概率问题

一个概率值如果可能性是70%，那么不可能性就是1-70%

一旦求出概率，就可以得到分类结果

解释：将任意输入映射到了[0,1]区间，我们在线性回归当中可以得到一个预测值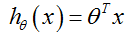（），但是线性回归是特例，这里的θ是随机取值的

再将该值映射到sigmoid函数当中，就完成了预测值到概率的转换问题，也就是分类任务

ps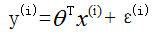：这个函数对应的是实际值，线性回归所要做的事是，在误差最小概率最大的地方求出θ，是概率的问题，而不是实际值的问题，这里是讨论的并不是线性回归，线性回归只是回归的一种特例；

这里是随机θ之后，为了得到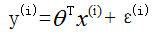的最小值，化成的概率问题，只是单纯地变为概率问题，再由θ和新的x得到预测值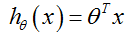，这里说的预测值就是这个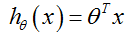

 

预测函数：

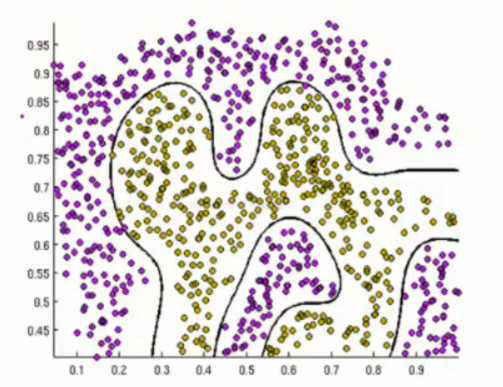
这里引入概率函数相当于线性回归中的将实际值转换为高斯分布概率函数

分类任务：，

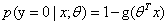
整合后：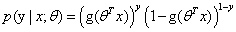

似然函数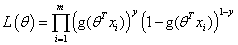：，要让所有的样本满足θ准确最大概率，就是误差最小的概率，也就是上节课所说的损失函数最小的概率，所以要进行累乘。

对数似然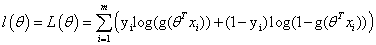：，同线性回归一样，用对数将累乘转换为求和。

对于似然函数是求梯度上升时的最大值，引入转换为梯度下降任务

则

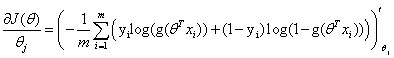化简得：

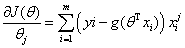
i表示第几个样本，j表示样本的第几个特征，一个样本有N个特征

 

这样做的目的是，找到一组θ值，使得\(J(\Theta)\)最小，则\(J(\Theta )\)对\(\Theta\) 求导，得出\(\Theta\)的方向，然后一步步的去试\(\Theta\)，

当\(\Delta \Theta\)的变化率很小的时候，我们可以认为找到了最小的$\Theta$

 

参数更新：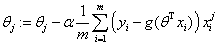

α是步长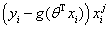，是更新的方向，也就是求出来θ的导数

每走一步，θj就会更新一次，

例如在python中写一个for循环，循环体就是θj = θj-α后面那一串，

则θj在循环结束后，就会得到最优值

多分类：

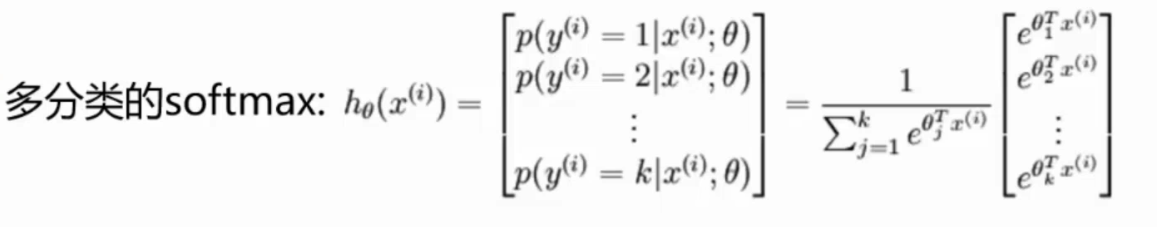，后期神经网络再介绍

 

总结：

逻辑回归相当于随机取θ，然后算出预测值，将预测值带入到sigmoid函数中，转换为概率问题，求出损失函数最小的概率，如何求出最小的概率？

并不是让导数等于0，而是先求出θ偏导的方向，一次取一个θ，再带入到参数更新中，因为α是步长，后面那一串是方向，有了步长和方向，就可以得到新的θ，最后求新老θ的差值

如果导数越接近于0的时候，那么差值就越小，θ就会越收敛，这样就会求出θ。