001-线性回归
如果有一组样本
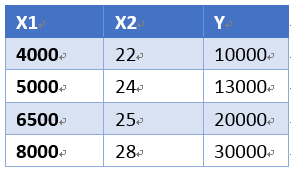
要根据以后的x1，x2来预测以后未知的y
相当于拟合一个由θ1x1，θ2x2的平面hθ（x）来估计Y值
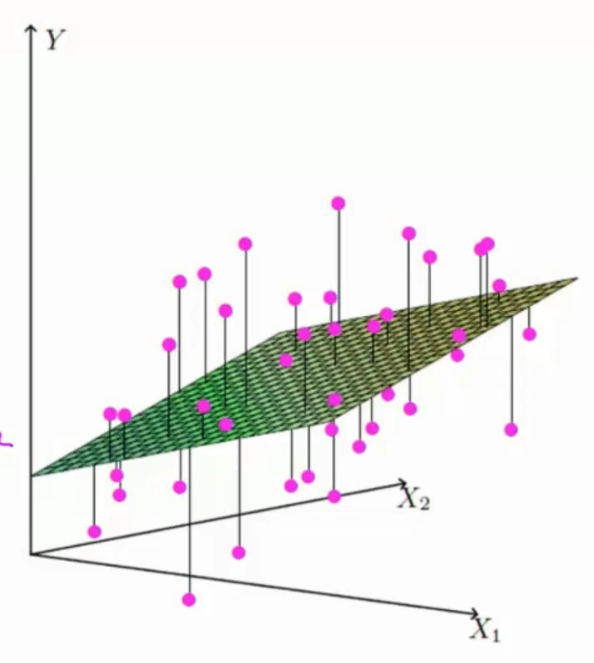
是偏置项
如果样本的特征无限增多，也就是x项有n多个
相当于
令x0=1
则有
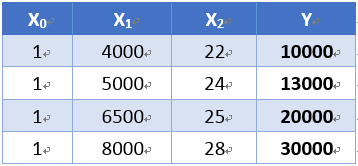
矩阵比较高效，需要转换为矩阵，则
化为矩阵：
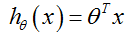
预测值和真实值之间必定存在误差
则设，误差为：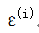
则每个样本的实际值为：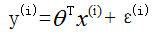
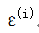的概率密度服从正态分布，独立并且相同分布
均值为0，方差为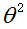
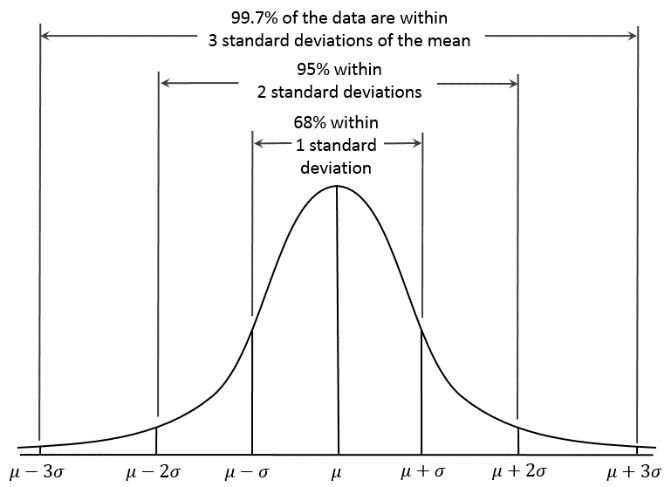
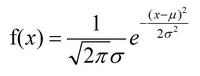
则此处的μ为0，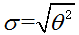
独立：每一组x的误差都与另外一组x的误差无关
相同分布：属于同一组数据或同一个作用域或x来自于同样一个地方的
因为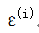服从高斯分布
则：
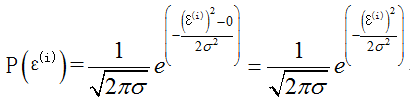
因为：
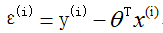
则：
似然函数：根据样本来估计参数值，也就是说，什么样的参数跟数据组合后恰好是真实值
目标是让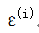越小越好，也就是说，让真实值和估计值越接近越好，或者是真实值与估计值相同的概率越高越好
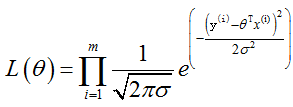
累乘关系，为什么是累乘？
因为这里是要满足所有样本数据，相当于与的关系 ，
因为前面说，误差的均值是0，并且满足高斯分布，
那么高斯分布在均值处，概率最大，均为为0，误差为0
也就是说所有的误差分布的概率相乘之后，越大越好，对应的点就是误差为0
对数似然：为什么要取对数？因为加法比乘法简单
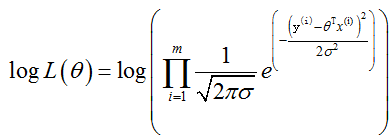
因为：
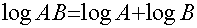
则可以化为：
化简：
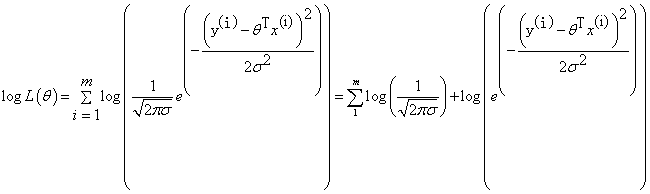
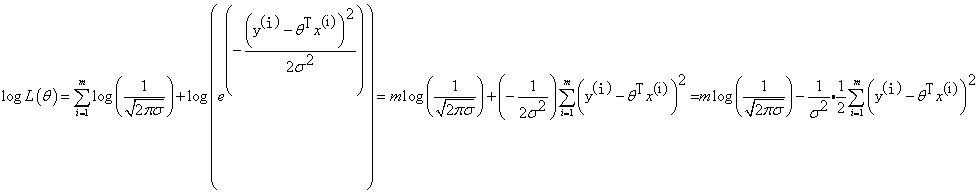
前面说过，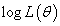
越大越好
则
可看做常数而且为正数
当
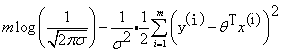时
则让
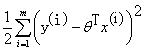最小
就可以有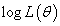最大
令
称为最小二乘法
真实值减去预测值的函数，
这里也说明，真实值减去预测值越小越好，得到的误差最小的概率也就越大，
这里一直是概率问题，不是实际误差值
这里的θ，x，y都是矩阵
展开后化简为：
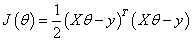
这里矩阵X，y都是已知量
则对θ求偏导，导数为0时，有θ最小值
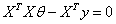
则
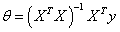时
有θ最小值
X就是样本，Y也是样本
则可以求出θ
评估方法：
残差平方和越小越好，也就是真实值和预测值越接近，
则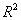
越接近1，就说明这个模型是越好的
数学不要过一遍，用到哪里去看哪里就行，过一遍也不一定全都能记住。
唐宇迪机器学习视频笔记——线性回归算法原理推导
