HDU5733 tetrahedron

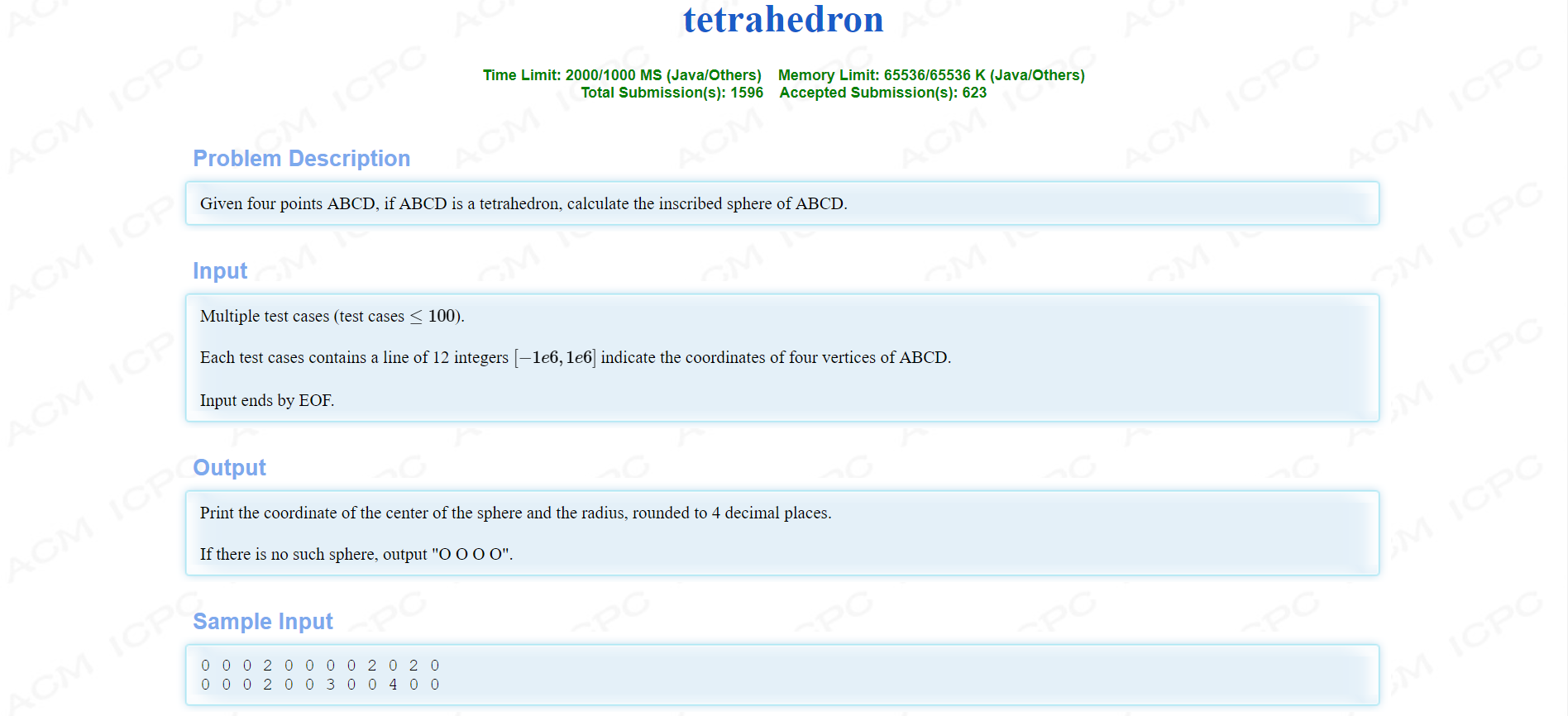
计算几何题 给出四个点 求这四个点构成三棱锥的内切球的三维坐标和半径

先判断这个四个点是否共面 共面就直接输出O O O O 然后就用公式啦

注意scanf的时候要用%lf 最开始用的%f就各种出现nan和inf

这里贴个链接公式的链接 http://www.docin.com/p-504197705.html?qq-pf-to=pcqq.c2c

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

class point{
public:
    double x;
    double y;
    double z;
    point(double xx = 0, double yy = 0, double zz = 0){
        x = xx;
        y = yy;
        z = zz;
    }
};

point operator -(point a, point b){
    return point(a.x - b.x, a.y - b.y, a.z - b.z);
}

point cross_product(point a, point b){
    return point(a.y * b.z - a.z * b.y, a.z * b.x - a.x * b.z, a.x * b.y - a.y * b.x);
}

double dot_product(point a, point b){
    return a.x * b.x + a.y * b.y + a.z * b.z;
}

double Herons_formula(double a, double b, double c){
    double p = (a + b + c) / 2;
    return sqrt(p * (p - a) * (p - b) * (p - c));
}

double dist(point a, point b){
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y) + (a.z - b.z) * (a.z - b.z));
}

int main(){
    point A, B, C, D;
    point AB, AC, AD;
    double s1, s2, s3, s4;
    double ab, ac, ad, bc, bd, cd;
    double x, y, z, r;
    double V;
    while (scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf", &A.x, &A.y, &A.z, &B.x, &B.y, &B.z, &C.x, &C.y, &C.z, &D.x, &D.y, &D.z) != EOF){
        AB = A - B;
        AC = A - C;
        AD = A - D;
        V = abs(dot_product(cross_product(AB , AC), AD) / 6);
        if (V == 0){
            cout<<"O O O O"<<endl;
            continue;
        }
        ab = dist(A, B);
        ac = dist(A, C);
        ad = dist(A, D);
        bc = dist(B, C);
        bd = dist(B, D);
        cd = dist(C, D);
        s1 = Herons_formula(bc, bd, cd);
        s2 = Herons_formula(ac, ad, cd);
        s3 = Herons_formula(ab, ad, bd);
        s4 = Herons_formula(ab, ac, bc);
        x = (s1 * A.x + s2 * B.x + s3 * C.x + s4 * D.x) / (s1 + s2 + s3 + s4);
        y = (s1 * A.y + s2 * B.y + s3 * C.y + s4 * D.y) / (s1 + s2 + s3 + s4);
        z = (s1 * A.z + s2 * B.z + s3 * C.z + s4 * D.z) / (s1 + s2 + s3 + s4);
        r = (V * 3) / (s1 + s2 + s3 + s4);
        printf("%.4lf %.4lf %.4lf %.4lf\n", x, y, z, r);
    }
    return 0;
}