LeetCode | 236. 二叉树的最近公共祖先
原题(Medium):
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
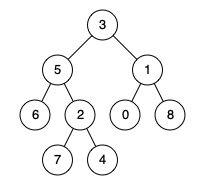
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
思路:递归
想到这个思路的人肯定很牛。所需代码非常简洁。我虽然也想到递归,但没想过可以这么简单。
这题需要从根节点出发自上而下的遍历节点,寻找p跟q节点,但问题不是找这两个节点,而是找这两个的节点的最近公共祖先节点,所以要把找到p或q节点这个信息通知父节点,告知父节点你的左或右子树有目标节点。但是通过根节点我们只能往下寻找,不能返回,所以唯有递归的方式能把子节点的情况告知父节点。
树的根节点作为当前节点出发,只要当前节点不是p或q节点,就分别进入左子节点和右子节点(把这两个节点分别作为根节点进入左子树和右子树)去继续寻找p节点和q节点,只要发现当前节点就是p或q其中一个,就立马返回,告知其父节点,p或q节点在左或右子树,如果在父节点处发现其左子树包含q、右子树包含p,或者左子树包含p、右子树包含q的情况,就意味着这父节点就是最近公共祖先节点。如果并不是,说明该父节点并不是最近祖先(只有一个目标节点在其左或右子树,另一个不在),那么继续把发现目标节点这个信息往上返回,告知其父节点的父节点。
特殊情况就是 p就是q或q就是p的最近祖先。这时我们的递归结果只能发现一个目标节点在其左或右子树上,而不见另一个目标节点的踪影,因为我们是找到就立即返回,而另一个节点是在第一个节点的下面,所以是不可能找到另一个目标节点的,但找到这个节点不就是最近公共祖先了吗?所以直接返回该结点就好了。
1 TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { 2 //找到其中一个目标节点就是返回,告知父节点 3 if(root == NULL | root == p | root == q) return root; 4 //递归进入左右子树寻找两个目标节点,使用指针记录递归返回的结果(目标节点是否在左或右子树上) 5 TreeNode* left = lowestCommonAncestor(root->left, p, q); 6 TreeNode* right = lowestCommonAncestor(root->right, p, q); 7 //判断两个目标节点是不是一个在当前节点的左子树一个在当前节点的右子树,如果是说明当前节点是最近公共祖先,返回自己; 8 //如果不是,而是只有其中一个,那就返回那个,告知父节点 9 return left == NULL ? right : (right == NULL ? left : root); 10 }



