LeetCode | 221. 最大正方形

原题（Medium）：

　　在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

　　

 

 

 

思路：动态规划

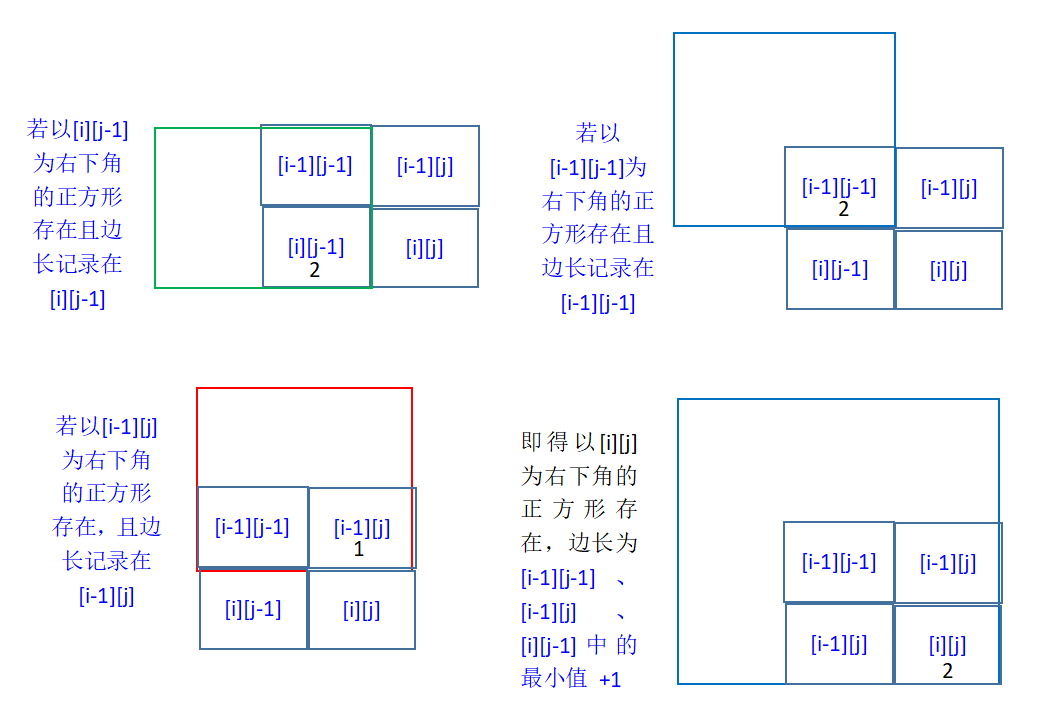
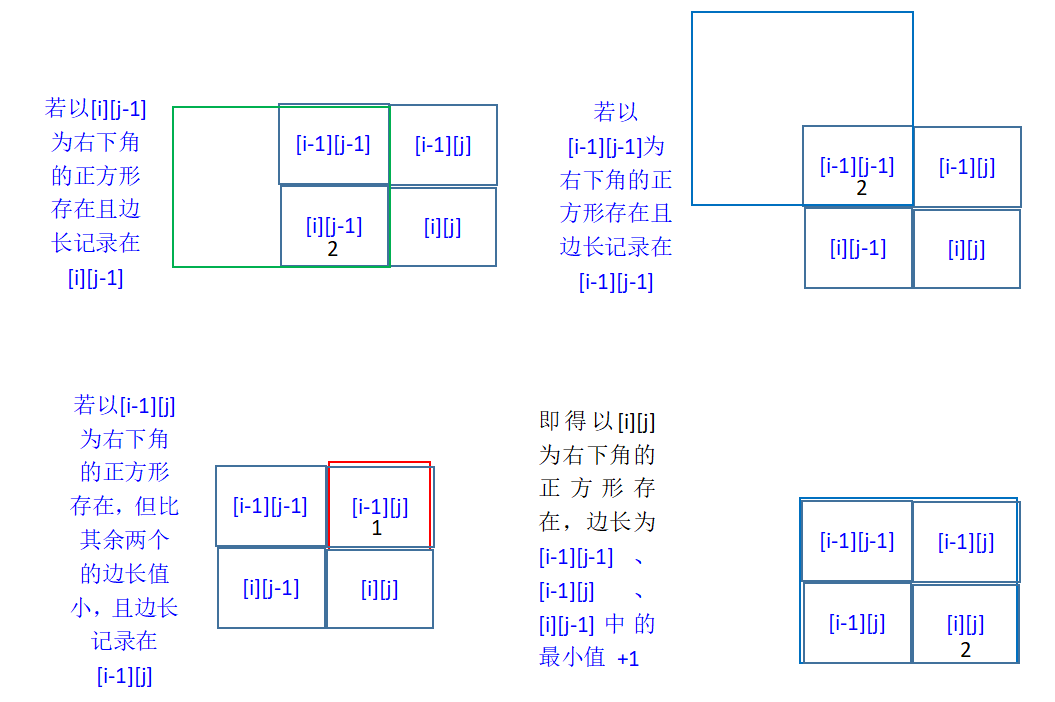
　　如果某一个点 [i][j] 的值为1，我们不妨可以假设它是一个正方形的右下角，且另起一个数组dp，记录该点所在的正方形的边长，即使有可能它周围点都是0，但它自己本身也是一个边长为1的正方形，所以这个假设是可行的。该点为右下角的正方形的最大边长，最多比它的上方，左方和左上方为右下角的正方形的边长多1。要想它是一个边长为3的正方形的右下角，那么它的左上[i-1][j-1]，左前[i][j-1]，上方[i-1][j]的点（这些点也被赋予了作为某一正方形右下角的意义，记录的是其所在的正方形的边长）在数组dp里的值也必须记录为2。如果它们其中有的点值为0或为1，说明以[i][j]为右下角且边长为2的正方形不存在，取这些点的最小值+1，即为点 [i][j] 所在的正方形的边长：

 

 

 

 

 

 

    int maximalSquare(vector<vector<char>>& matrix) {
        if(matrix.empty()) return 0;
        vector<vector<int>> dp(matrix.size(),vector<int>(matrix[0].size(),0));
        
        for(int i = 0;i<matrix[0].size();i++)
            if(matrix[0][i] == '1')
                dp[0][i] = 1;
            else dp[0][i] = 0;
        for(int i = 0;i<matrix.size();i++)
            if(matrix[i][0] == '1')
                dp[i][0] = 1;
            else dp[i][0] = 0;
        
        for(int i = 1;i<matrix.size();i++)
            for(int j = 1; j <matrix[i].size();j++)
            {
                if(matrix[i][j]=='1')
                {
                    int min = dp[i][j-1] < dp [i-1][j] ? dp[i][j-1] : dp[i-1][j];
                    min = min< dp[i-1][j-1] ? min : dp[i-1][j-1];

                    dp[i][j] = min+1;
                }
            }
        
        int max = dp[0][0];
        for(int i = 0;i<matrix.size();i++)
            for(int j =0; j <matrix[i].size();j++)
                max = max > dp[i][j] ? max : dp[i][j];
        return max*max;
    }