LeetCode | 142. 环形链表 II

原题（Medium）：　

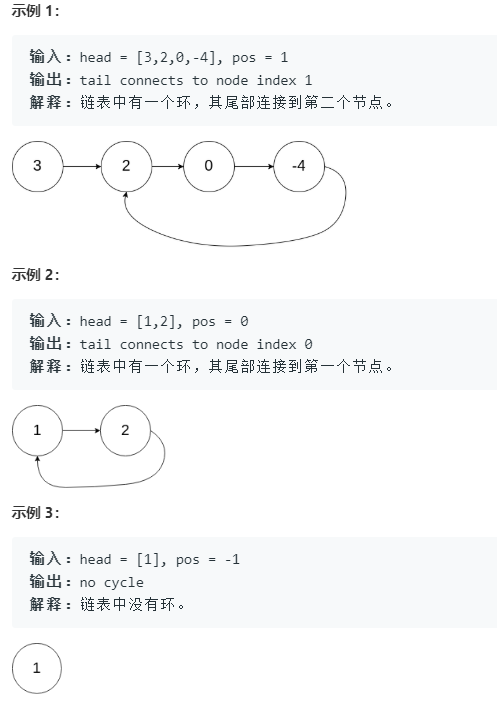
　　给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

　　为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

　　说明：不允许修改给定的链表。

　　

 

 

思路：

　　首先要考虑的就是怎么发现一个链表是否有环，一个比较普遍的解法就是：快慢指针，定义两个指针：一个快指针，快指针每次跨链表的两个节点；一个慢指针，慢指针每次指向下一个节点。如果链表有环，那么两指针迟早会相遇，从而发现有环而结束比遍历，如果没指针，快指针就会到达链表尾部而结束遍历。

　　接下来就是难点了，如何找到入环的节点，我们假设入环的节点与链表的首节点距离为a，然后假设入环的节点与快慢指针相遇的那个结点的距离为b，那么在两指针相遇时，我们可以知道快指针走过的距离为a+x圈+b，而慢指针走过的距离为a+y圈+b，且有一个重要的信息就是，在两指针相遇时，快指针走过的距离是慢指针的两倍。就是说a+x+b  = 2(a+y+b) 还有一个条件就是快指针比慢指针多走的路程一定是环长的整数倍（假设是n倍），这是肯定的，因为a的长度两个节点都会走，那么快指针比慢指针多出来的长度就是快的比慢的多走很多圈，即2(a+y+b)  - (a+y+b)  = a+b+y圈 = n 圈：入环节点与链表的首节点距离（a）+入环节点到相遇点之间的距离（b）是环的整数倍（n - y圈），现在我们知道两个指针都在离入环节点距离为b的那个相遇点，而现在a+b是环长度的整数倍，就是说如果慢指针再走a步，就等于慢指针再走了一次a+b的路程，（1圈也好，n圈也好，都是）回到了入环结点的位置，但是问题是，我们不知道a是多少啊？

　　我们可以再定义一个指针指向首节点，该指针走a步的同时慢指针也走a步，两者就相遇啦，相遇的节点就是入环节点。

ListNode *detectCycle(ListNode *head) {
    if (head == NULL) return NULL;
    ListNode* fast = head;
    ListNode* slow = head;
    bool hasCycle = false;
    //首先，快慢指针判断是否有环
    while (fast&& fast->next != NULL)
    {
        fast = fast->next->next;
        slow = slow->next;
        if (fast == slow)
        {
            hasCycle = true;
            break;
        }
    }
    //没环，结束
    if (!hasCycle) return NULL;
    //有环，两指针同时走，必在a步后相遇，相遇点为入环节点
    ListNode* q = head;
    while (q != slow)
    {
        q = q->next;
        slow = slow->next;
    }
    return q;
}