LeetCode | 139. 单词拆分

原题（Medium）：　

　　给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

　　说明：

• 拆分时可以重复使用字典中的单词。
• 你可以假设字典中没有重复的单词。

　　

 

 

 

思路：动态规划

　　这题有个陷阱，需要特别注意，就是非空字符串s的字母是可以被重复使用的，例如 s = "cars"， wordDict = ["car", "ca", "rs"]，输出是true，cars可以被分为car和rs，重复使用了字母r。就是因为这点这题的难度就大了很多。至少不能用类似双指针的暴力解法了。

　　因为这点，说明字符串s的任何长度的子串都能作为一个单词，亦如"cars"，它的组合有c、ca、car、cars、a、ar、ars、r、rs、s。我们可以用一数组记录以任意长度子串能否拆分为单词的可能，即一bool数组dp，而dp[i]代表字符串s从s[0]开始到s[i]这一个子串能否拆分为单词的可能，而dp[i]是否成立（true or false），取决于dp[j]是否为（true）和s[j+1]到s[i]组成的子串能否在字典中找到对应的单词，这段话可能有点难以理解，可以配合图：

 

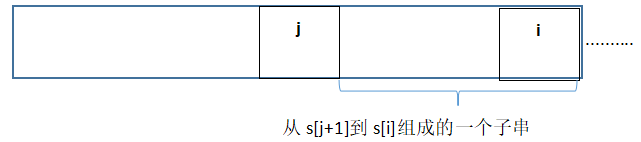
 　　dp[j]如果为true，说明从s[0]开始到s[j]的这一个子串能被拆分为单词，那么此时dp[i]要想成立，只需看能否在字典中找到与s[j+1]到s[i]组成的子串匹配的单词了，找到就dp[i]为true，找不到就j++，直到j等于i为止。如果dp[j]为false，那么即使s[j+1]到s[i]组成的子串能在字典中被找到也无济于事，所以如果dp[j]为false,j直接++。那么j从0开始，直到i为止。这样s[0]开始到s[i]这一个子串能否拆分为单词的所有可能性都被我们尝试过了（如果中途有成立的情况就可以跳出了）。那么i从0开始到整个字符串末尾结束，整个字符串能否被拆分为单词的所有可能性都被我们尝试过了。

　　不过超出字典最长单词长度的距离是可以忽略的，例如字典最长单词长度为4，那么j和i的距离只要大过4就没有意义，如果i已经大于4了，j就可以直接从i-4开始。所以我们需要先获取字典最长单词的长度。

bool wordBreak(string s, vector<string>& wordDict) {
    //dp数组下标从1开始，有利于计算子串
    vector<bool> dp(s.size() + 1, false);
    dp[0] = true;
    int maxLength = 0;
    auto beg = wordDict.begin();
    auto end = wordDict.end();
    //获取字典最长单词长度
    for (int i = 0; i < wordDict.size(); i++)
        if (maxLength < wordDict[i].length())    
            maxLength = wordDict[i].length();
    
    //在前maxLength个字符组成的字符串时，j都从0开始，如果i已经大于maxLength了，j就从i - maxLength开始
    for (int i = 1; i <= s.length(); i++)
        for (int j = std::max(i - maxLength, 0); j < i; j++)
            //取决于dp[j]是否为（true）和s[j+1]到s[i]组成的子串能否在字典中找到对应的单词
            if (dp[j] && find(beg, end, s.substr(j, i - j)) != wordDict.end())
            {
                //substr的作用是从字符串s的j号元素出发（从0开始算的j，但不包括j），之后的i - j个元素形成一个子串返回。
                dp[i] = true;
                break;
            }
    return dp[s.size()];
}