LeetCode | 105. 从前序与中序遍历序列构造二叉树

原题（Medium）：　

　　根据一棵树的前序遍历与中序遍历构造二叉树。

　　注意:
　　　　你可以假设树中没有重复的元素。

　　

 

思路：

　　前序遍历，其数组的分布应为[根结点，左子树结点，右子树结点]。

　　中序遍历，其数组分布应为[左子树结点，根结点，右子树结点]。

　　那么，从前序遍历数组出发，第一个元素即为根结点的值，在中序数组中获取该结点的位置，该位置的前面即为根结点的左子树，后面即为根结点的右子树。区分了中序数组的左中右分布后，我们还要知道前序数组的分布：从中序数组的左子树部分的第一个元素开始，计算到根结点位置的距离L。在前序数组中，根结点开始的L个元素为左子树部分，剩余的为右子树部分。

 

 

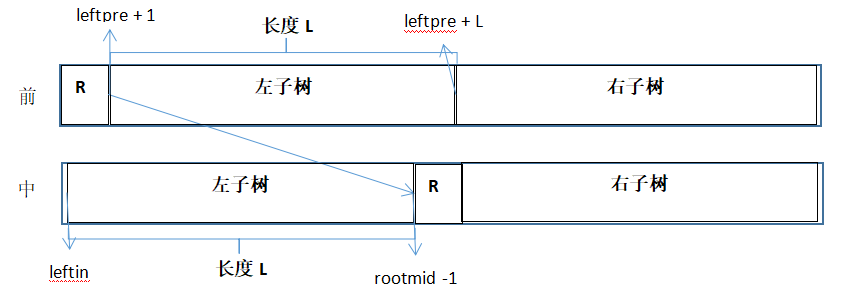
　　之后，确定了两个数组的左右子树的分布后，就可以递归了，把左子树看作一棵完整的树，继续往下确定其左右子树的分布，右子树同理。至于怎么把子树看作一棵完整树，得知前序遍历子树的范围（例如左子树前序范围为[leftpre+1, leftpre+L]）和中序遍历子树的范围（例如左子树的中序范围为[leftin, rootmid-1]），把这两个范围看作新的前序和中序数组：

 

 

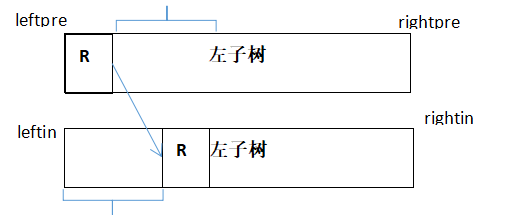
　　在确定左右子树的之前，先把根结点记录在二叉树里，按照递归，根结点值就是前序数组范围的第一个元素。

//leftpre、rightpre为当前树的前序范围，leftin、rightin为当前树的中序范围，
TreeNode* helper(vector<int>& preorder, vector<int>& inorder, int leftpre, int rightpre, int leftin, int rightin)
{
    if (leftpre <= rightpre && leftin <= rightin)
    {
        TreeNode* root = new TreeNode(preorder[leftpre]);    //前序范围的第一个元素就为当前树根结点
        //在中序数组中确定根结点的位置，顺便找出当前树的左子树的长度left
        int rootmid = leftin;
        while (inorder[rootmid] != preorder[leftpre]) rootmid++;
        int left = rootmid - leftin;

        //那么左子树的前序范围就是[leftpre+1, leftpre+left]，中序范围就是[leftin, rootmid-1]
        root->left = helper(preorder, inorder, leftpre + 1, leftpre + left, leftin, rootmid - 1);
        //那么左子树的前序范围就是[leftpre+left+1, rightpre]，中序范围就是[rootmid+1, rightin]
        root->right = helper(preorder, inorder, leftpre + left + 1, rightpre, rootmid + 1, rightin);
        return root;
    }
    else
        return NULL;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    return helper(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
}