LeetCode | 114. 二叉树展开为链表
原题(Medium):
给定一个二叉树,原地将它展开为链表。

根据题意,原地展开的意思是,按照中序遍历的顺序(中左右)把二叉树的结点逐一放到树的右节点上。
思路:
我们已经知道,展开为链表后各节点顺序就是二叉树中序遍历的顺序,那么于一个节点而言,展开后,原本在其左子树节点肯定在原本其右子树的前面,例如:
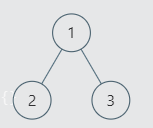
其展开后节点2肯定在结点3前面。结果为: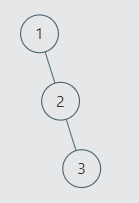
那么,用左节点取代右节点的位置,这于根结点而言,应该是没错的,是合乎顺序的,但是在这之前,我们肯定要考虑右节点的去向,我们可以以题目的例子为例:
我们用左子树取代右子树,右子树暂时孤立,即:
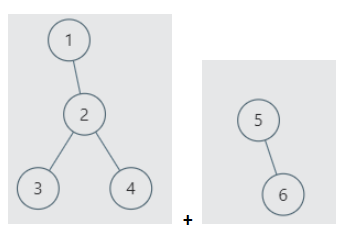
那么按照中序遍历的顺序(节点内的数字就代表中序遍历的顺序),这右子树应该落在哪里呢?显然,应该节点4的右节点上:

而于根结点1而言,节点4是一个什么节点呢?我们能否根据特征找到这个节点然后把右子树接上去呢?其实我们要找的就是根节点的左子树的最右节点(节点4就是最右节点),按照中序遍历的顺序,这个最右节点就是在遍历到根节点之前的最后一个节点(就是说遍历完该节点后下一个被遍历的节点就是根节点),那么把右子树接到该最右节点的右子树上,就非常合理了。至于怎么找到它也非常容易,因为我们已经知道它是左子树的最右节点了。从左子树的第一个节点开始一直往其右节点遍历,直到右节点为空。
再经历了上述的变换后,我们还没有解决问题,可以看到,虽然节点1的下的所有节点已经移动到右子树,但右子树里仍有不合题意的节点,显然需要我们进入右子节点,以节点2为根节点,继续考虑其左右子树的情况,进行类似的变换。可以得知,这是递归的思路,但实现的方法可以是递归,也可以不是递归。
1 void flatten(TreeNode* root) { 2 while (root != nullptr) { 3 if (root->left != nullptr) { 4 auto most_right = root->left; // 如果左子树不为空, 那么就先找到左子树的最右节点 5 while (most_right->right != nullptr) most_right = most_right->right; // 找最右节点 6 most_right->right = root->right; // 然后将跟的右孩子放到最右节点的右子树上 7 root->right = root->left; // 这时候跟的右孩子可以释放, 因此我令左孩子放到右孩子上 8 root->left = nullptr; // 将左孩子置为空 9 } 10 root = root->right; // 继续下一个节点 11 } 12 return; 13 }