C++边双缩点，Redundant Paths 分离的路径

一道比较简单的 关于边双的题，个人感觉难度不大。
求出整个图的边双，根据边双的定义我们可以延伸出 边双的任两个点都有至少两种路径来互相抵达（因为其不存在割边） 。不妨将每个边双缩成一个点，样例中的图便变成了一棵树：

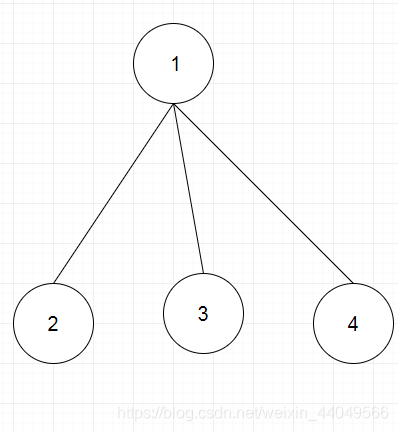
为什么呢？因为缩了点之后的图如果存在环，这个环便又可以构成一个边双了。

我们发现只要 将所有的叶子节点（度为1）的节点连起来，整个图便就构成了一个边双。那么我们的做法就很明确了，选取一个度不为1的点作为根，统计度为1的节点的数量n,答案便是(n+1)/2.

#include <iostream>
#include <vector>
#include <stack>
#include <cstring>
#include <cstdio>
using namespace std;

#define N 5010
#define M 10010
#define LL long long

struct node {
	int to,no;
	node () {};
	node (int T,int No) {
		to=T;no=No;
	}
};

LL flag,ans,value[M],n,m,num,cntn,DFN[N],IsCut[M],low[N];
vector <node> G[N];

LL read() {
    LL f=1,s=0;char a=getchar();
    while(!(a>='0'&&a<='9')) { if(a=='-') f=-1 ; a=getchar(); }
    while(a>='0'&&a<='9') { s=s*10+a-'0'; a=getchar();}
    return f*s;
}

int min(int a,int b) {
	if(a<b) return a;
	return b;
}

void Tarjan(LL u,LL fano) {
	DFN[u]=low[u]=++num;
	for(LL i=0;i<G[u].size();i++) {
		LL v=G[u][i].to,vno=G[u][i].no;
		if(!DFN[v]) {
			Tarjan(v,vno);
			if(low[v]>DFN[u]) {
				IsCut[vno]=1;
				cntn++;
			}
			low[u]=min(low[u],low[v]);
		}
		else if(DFN[u]>DFN[v] && vno!=fano)
			low[u]=min(low[u],DFN[v]);
	}
}

bool vis[N];
int belong[M],rel[N],cntno,cnt=1;

void init() {
	memset(low,0,sizeof(low));
	memset(DFN,0,sizeof(DFN));
	memset(IsCut,0,sizeof(IsCut));
	memset(vis,0,sizeof(vis));
	cin>>n>>m;
	for(int i=1;i<=n;i++) 
		G[i].clear();
	cntno=cntn=0;
	for(int i=1,u,v,w;i<=m;i++) {
			u=read();v=read();
			G[u].push_back( node (v,cnt) );
			G[v].push_back( node (u,cnt++) );
		}
	
}



int dfs(int u) {
	belong[u]=cntno;
	for(int i=0,v,vno;i<G[u].size();i++) {
		v=G[u][i].to,vno=G[u][i].no;
		if(!IsCut[vno] && !belong[v])
			dfs(v);
	}
}

bool book[N][N];

int main() {
	init();
	Tarjan(1,-1);
	for(int i=1;i<=n;i++)
		if(!belong[i]) {
			cntno++;
			dfs(i);
		}
		
	//cout<<cntno<<endl;
	for(int i=1;i<=n;i++)
		for(int j=0;j<G[i].size();j++) {
			int x=belong[i],y=belong[G[i][j].to];
			if(x!=y ) {
				rel[x]++; //rel统计边双的度
			}
		}
	for(int i=1;i<=n;i++)
		if(rel[i]==1)
			ans++;
	cout<<(ans+1)/2<<endl;
}