C++食物链【NOI2001】 并查集+建虚点

B. 食物链【NOI2001】
内存限制：256 MiB
时间限制：1000 ms
标准输入输出
题目类型：传统
评测方式：文本比较
题目描述
动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。

现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这N个动物所构成的食物链关系进行描述：

第一种说法是"1 X Y"，表示X和Y是同类。

第二种说法是"2 X Y"，表示X吃Y。

此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

1）当前的话与前面的某些真的话冲突，就是假话；

2）当前的话中X或Y比N大，就是假话；

3）当前的话表示X吃X，就是假话。

你的任务是根据给定的N（1≤ N ≤50,000）和K句话（0≤K≤100,000），输出假话的总数。

输入格式
第一行是两个整数N和K，以一个空格分隔。

以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。

若D=1，则表示X和Y是同类。

若D=2，则表示X吃Y。

输出格式
只有一个整数，表示假话的数目。

样例
样例输入
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
样例输出
3
数据范围与提示
100 7 1 101 1 假话 2 1 2 真话 2 2 3 真话 2 3 3 假话 1 1 3 假话 2 3 1 真话 1 5 5 真话

首先考虑题目中所说的3种矛盾情况中的后两种，都很好判断，关键是如何判断当前的话是与前面的话冲突的。

这里我们先给出两个定理以方便判断一些关系：

一.因为三个种族都有一个且且仅有一个能吃的种族。如果动物A能吃B，动物C也能吃B，那么说明 A和C便是同一个种族 ，否则这个关系就是矛盾的。
二.如果A能吃B，B能吃C，那么可以得出C能吃A，也就是如下这个关系：

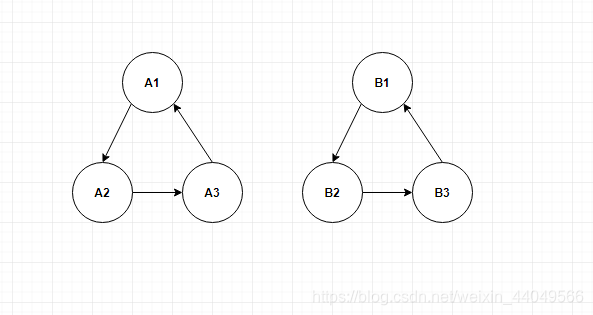
对于单个点\(A_{1}\)，我们可以给它建两个虚点\(A_{2},A_{3}\)，并且假设出这三个点之间的关系，\(A_{1}\)吃\(A_{2}\)，\(A_{2}\)吃\(A_{3}\)，\(A_{3}\)吃\(A_{1}\)。同样在假设有一个点\(B_{1}\)，它同样也有这些虚点。我们可以使用一个有向图来表示这个关系以方便理解。

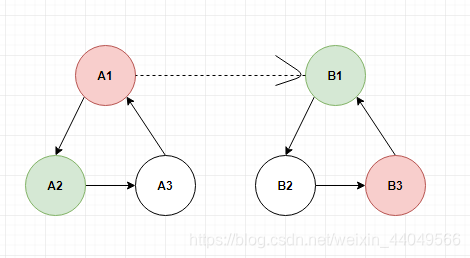
当\(A_{1}\)可以吃掉\(B_{1}\)时，我们可以发现\(A_{1}\)和\(B_{3}\)成了同类（参考定理1，同样根据定理1，我们还可以得出\(A_{2}\)和\(B_{1}\)是同类，如果是\(B_{1}吃A_{1}则相反\)）。

根据定理2，我们可以得出\(B_{1}\)可以吃掉\(A_{3}\)，同时它也可以吃掉\(B_{2}\)，所以\(A_{3}\)和\(B_{2}\)也是同类..

如果我们判断两个点是同类，则可以将他们放入同一个并查集中。需要注意的是，虚点只是用来帮助我们判断动物之间的关系的，并没有实际含义。

那么如何判断一句话是矛盾的呢，我们可以分情况讨论。
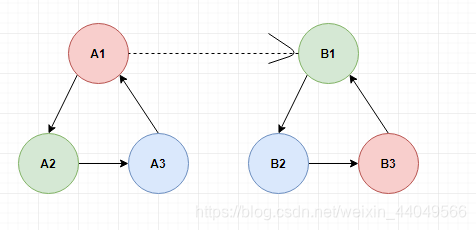
如果\(A_{1}\)可以吃\(B_{1}\)，结合图片，我们可以发现\(A_{1}\)和\(B_{2}\)，依此类推\(B_{1}\)和\(A_{3}\)也不是同类，\(A_{1}\)和\(B_{1}\)更不是同类。我们便可以使用并查集，如果上述两者在同一个并查集，便说明它们是矛盾的。

同理如果\(A_{1}\)和\(B_{1}\)是同类的话也可以这么考虑。需要注意的是，所以情况都要考虑完，实点和虚点入并查集时情况也要考虑完（不然就是WA,XD）。

可能有些同学要问为什么要判断两个点在同一个并查集，来判断这句话是不是矛盾的，而不是判断两个点不在同一个并查集，也就是

if(find(A1) == find(B2)） 矛盾

和

if(find(A3) != find(B2)) 矛盾

的区别。

因为我们建立的是虚点，一开始所有的点都在独立的并查集，直接判断便会误判。
可以这么理解，我们在条件不够的情况下，第二种方式是“猜测”，第一种方式则是“尽量满足关系，最后不得不判断矛盾”。

关于建立虚点，设当前有n个实点,\(A\)的两个虚点可以用\(A+n\)和\(A+2*n\)来表示.

代码

#include <iostream>
#include <cstdio>
#include <string>
#include <map>
using namespace std;

#define N 50010

int fa[N*3],n,k,ans;

int find(int x) {
    if(fa[x]!=x) return fa[x]=find(fa[x]);
    return x;
}

int main() {
    cin>>n>>k;
    for(int i=1;i<=n*3;i++) fa[i]=i;
    for(int i=1,a,b,c;i<=k;i++) {
        cin>>a>>b>>c;
        if(b>n || c>n || (a==2 && b==c)) { ans++; continue; }
        if(a==2) {
            if(find(b)==find(c)||find(b+n*2)==find(c)||find(c+n)==find(b)) ans++;
            else {
                fa[find(b+n)]=find(c);
                fa[find(b)]=find(c+2*n);
                fa[find(c+n)]=find(b+2*n);
            }
        }
        if(a==1) {
            if((find(b+n) == find(c)) ||(find(b+2*n) == find(c))) ans++;
            else {
                fa[find(b+2*n)]=find(c+2*n);
                fa[find(b+n)]=find(c+n);
                fa[find(b)]=find(c);
            }
        }
    }
    cout<<ans;
}