线段tree~讲解+例题
最近学习了线段树这一重要的数据结构,有些许感触。所以写一篇博客来解释一下线段树,既是对自己学习成果的检验,也希望可以给刚入门线段树的同学们一点点建议。
首先声明一点,本人是个蒟蒻,如果在博客中有什么不当的地方,还请大佬们指出来,感激不尽!
一.为什么要用线段树?
既然线段树对于初学者来说,不是那么好学也不好写,那么为什么要用到线段树,是一个问题。
下面,我们先看一个问题:
100000个正整数,编号从1到100000,用A[1],A[2],A[100000]表示。
修改:1.将第L个数增加C (1 <= L <= 100000)
统计:1.编号从L到R的所有数之和为多少? 其中1<= L <= R <= 100000.
我们很容易就想到暴力算法,但是在实现后,我们发现程序运行起来很慢。
那么有没有什么解决方法?答案当然是:线段树!
二.什么是线段树?
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。(摘自百度百科)
便于对一段元素的查询与修改。
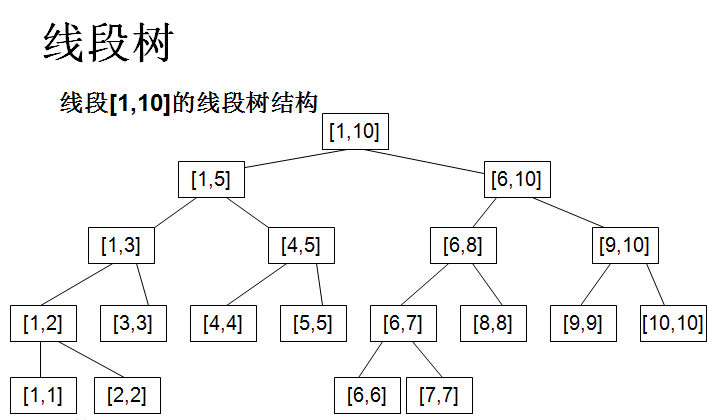
我们观察上图可以看出:
每一个叶子节点就是每个元素,每一个父节点都是对自己下面子节点的整合,而根节点就是对整个元素的整合。
学过分块的同学不难看出来,线段树就是在分块里面分块。
按理说分块能做的题,线段树绝大部分都能做,但是也有一部分题目所要求维护的元素信息是只有分块能维护的,在这里不细讲分块和线段树的区别,我们继续看线段树。
如果觉得我讲的不是很明白,在这里借用luogu 皎月半洒花(✿✿ヽ(°▽°)ノ✿)dalao的一段解释:

三.如何实现一颗线段树?
先说一下我的码风习惯:rt是当前节点,left是整棵树的左端点,right是右端点,mid是中点,l,r是代表要查询或者修改的区间范围,add是要更改的值,lson和rson我更喜欢在宏定义里搞定,build是递归建树,update是修改函数,query是查询函数,PushUP是上滤,PushDOWN是下滤
1.建造一颗线段树:
利用二叉树父子节点关系,父亲为i,孩子为2i+1,2i的特点,我们考虑递归建树(当然有其他更快的建树方法,在这里先不讲了)
在建树前,我们要先取出父节点的孩子,还需要一个PushUP函数来维护向上父子节点的关系。
在不同的要求下,PushUP的写法会不一样。这里以luogu P3372为例,PushUP函数的作用是求和。
1 #define ll long long 2 #define lson left, mid, rt<<1//左儿子 3 #define rson mid+1, right, rt<<1|1//右儿子 4 5 const int maxn = 100000; 6 ll ans[maxn<<2];//因为线段树所以要开四倍的空间 7 void PushUP(ll rt)//在这里的作用是求和,维护父子节点关系的正常 8 { 9 ans[rt] = ans[rt<<1] + ans[rt<<1|1]; 10 } 11 void build(ll left, ll right, ll rt) 12 { 13 if(left == right)//如果到了叶子节点 14 { 15 cin>>ans[rt];//输入叶子节点元素,即所给的序列元素 16 return; 17 } 18 ll mid = (left + right)>>1; 19 build(lson);//左右递归建树,并且维护上下父子关系 20 build(rson); 21 PushUP(rt); 22 }
2.线段树的基本操作
这里列举几个基本的线段树操作:
(1)单点修改
这里的单点修改是把一个新的值付给某个序列中的元素。
1 void update(ll s, ll add, ll left, ll right, ll rt) 2 { 3 if(left == right) 4 { 5 ans[rt] = add; 6 return ; 7 } 8 ll mid = (left + right)>>1; 9 if(s <= mid) update(s, add, lson); 10 else update(s, add, rson); 11 PushUP(rt); 12 }
(2)区间修改
因为是修改的是一个区间,所以我们会直接修改线段树中的父节点。于是我们需要一个下滤的操作,即PushDOWN,在这里我们为了让我们的线段tree跑的更快,我们引入了一个新的数组——lazy。(也可以叫染色col,但是我更喜欢懒标记这个叫法)懒标记实际上就是让子节点暂时处于不更新状态,用到的时候再更新。因为线段树的优点不在于全记录,而在于传递式记录。跑的才快。这里依旧是luogu P3372的区间修改,作用为给一段区间每个元素都加上一个数。
1 void PushDOWN(ll rt, ll mid, ll left, ll right) 2 { 3 if(lazy[rt]) 4 { 5 lazy[rt<<1]+=lazy[rt]; 6 lazy[rt<<1|1]+=lazy[rt]; 7 ans[rt<<1]+=(mid-left+1)*lazy[rt]; 8 ans[rt<<1|1]+=(right-mid)*lazy[rt];//给线段树更新lazy标记的值,因为是修改区间,所以要乘元素个数 9 lazy[rt]=0;//lazy已经传递完,归零 10 } 11 } 12 void update(ll l, ll r, ll add, ll left, ll right, ll rt) 13 { 14 if(l<=left&&r>=right) 15 { 16 lazy[rt]+=add; 17 ans[rt]+=add*(right-left+1); 18 return; 19 } 20 ll mid = (left+right)>>1; 21 PushDOWN(rt,mid,left,right);//下滤更改元素值 22 //这里注意判断左右子树跟[l,r]有无交集,有交集才递归 23 if(l<=mid) update(l,r,add,lson); 24 if(r>mid) update(l,r,add,rson); 25 PushUP(rt);//更新当前节点信息 26 }
(3)区间查询
区间查询l到r的和,返回res
ll query(ll l, ll r, ll left, ll right, ll rt)//这里变量的意义是查询l到r,左区间为left到mid,右区间为mid+1到right { ll res = 0; if(l<=left&&r>=right)//在区间内直接返回 { return ans[rt]; } ll mid = (left + right)>>1; PushDOWN(rt,mid,left,right); if(l<=mid) res += query(l,r,lson);//左子区间与[L,R]有重叠,递归 if(r>mid) res += query(l,r,rson);//右子区间与[L,R]有重叠,递归 return res; }
至于单点查询,你知道区间还能不会单点嘛~
四.线段树实战
1.luogu P3372 【模板】线段树1
区间修改,区间求和查询
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #define ll long long 5 #define lson left, mid, rt<<1 6 #define rson mid+1, right, rt<<1|1 7 using namespace std; 8 const int maxn = 100000; 9 ll n, m, ans[maxn<<2],lazy[maxn<<2]; 10 void PushUP(ll rt) 11 { 12 ans[rt] = ans[rt<<1] + ans[rt<<1|1]; 13 } 14 void build(ll left, ll right, ll rt) 15 { 16 if(left == right) 17 { 18 cin>>ans[rt]; 19 return; 20 } 21 ll mid = (left + right)>>1; 22 build(lson); 23 build(rson); 24 PushUP(rt); 25 } 26 27 void PushDOWN(ll rt, ll mid, ll left, ll right) 28 { 29 if(lazy[rt]) 30 { 31 lazy[rt<<1]+=lazy[rt]; 32 lazy[rt<<1|1]+=lazy[rt]; 33 ans[rt<<1]+=(mid-left+1)*lazy[rt]; 34 ans[rt<<1|1]+=(right-mid)*lazy[rt]; 35 lazy[rt]=0; 36 } 37 } 38 ll query(ll l, ll r, ll left, ll right, ll rt) 39 { 40 ll res = 0; 41 if(l<=left&&r>=right) 42 { 43 return ans[rt]; 44 } 45 ll mid = (left + right)>>1; 46 PushDOWN(rt,mid,left,right); 47 if(l<=mid) res += query(l,r,lson); 48 if(r>mid) res += query(l,r,rson); 49 return res; 50 } 51 void update(ll l, ll r, ll add, ll left, ll right, ll rt) 52 { 53 if(l<=left&&r>=right) 54 { 55 lazy[rt]+=add; 56 ans[rt]+=add*(right-left+1); 57 return; 58 } 59 ll mid = (left+right)>>1; 60 PushDOWN(rt,mid,left,right); 61 if(l<=mid) update(l,r,add,lson); 62 if(r>mid) update(l,r,add,rson); 63 PushUP(rt); 64 } 65 66 int main() 67 { 68 cin.sync_with_stdio(false); 69 cin>>n>>m; 70 ll p,x,y,k; 71 build(1,n,1); 72 while(m--) 73 { 74 cin>>p; 75 if(p==1) 76 { 77 cin>>x>>y>>k; update(x,y,k,1,n,1); 78 } 79 if(p==2) 80 { 81 cin>>x>>y; cout<<query(x,y,1,n,1)<<endl; 82 } 83 } 84 return 0; 85 }
2.luogu P1531 I Hate It
单点修改,区间最值查询
此题注意一点,对于是否确定修改,我们可以用max来搞定
1 #include <cstdio> 2 #include <algorithm> 3 #include <iostream> 4 #define lson left, mid, rt<<1 5 #define rson mid+1, right, rt<<1|1 6 #define ll long long 7 using namespace std; 8 const int maxn = 200000 + 10; 9 ll n, m, a[maxn], ans[maxn<<2]; 10 inline void PushUP(ll rt) 11 { 12 ans[rt] = max(ans[rt<<1],ans[rt<<1|1]); 13 } 14 15 void build(ll left, ll right, ll rt) 16 { 17 if(left == right) {scanf("%d",&ans[rt]); return ;} 18 ll mid = (left + right)>>1; 19 build(lson); 20 build(rson); 21 PushUP(rt); 22 } 23 void update(ll s, ll add, ll left, ll right, ll rt) 24 { 25 if(left == right) 26 { 27 ans[rt] = max(add,ans[rt]); 28 return ; 29 } 30 ll mid = (left + right)>>1; 31 if(s <= mid) update(s, add, lson); 32 else update(s, add, rson); 33 PushUP(rt); 34 } 35 ll query(ll l, ll r, ll left, ll right, ll rt) 36 { 37 38 if(l <= left&&right <= r){return ans[rt];} 39 ll mid = (left + right)>>1; 40 ll res = 0; 41 if(l <= mid) res = max(res,query(l, r, lson)); 42 if(r > mid) res = max(res,query(l, r, rson)); 43 return res; 44 } 45 int main() 46 { 47 int a,b; 48 char c; 49 scanf("%lld%lld", &n, &m); 50 build(1,n,1); 51 for(int i = 1; i <= m; i++) 52 { 53 cin>>c; 54 if(c == 'U') 55 { 56 cin>>a>>b; 57 update(a,b,1,n,1); 58 } 59 if(c == 'Q') 60 { 61 cin>>a>>b; 62 printf("%lld\n",query(a,b,1,n,1)); 63 } 64 } 65 return 0; 66 }
3.luogu P2068 统计和
单点修改 区间求和查询
1 #include <cstdio> 2 #include <iostream> 3 #define lson left , mid , rt << 1 4 #define rson mid + 1 , right , rt << 1 | 1 5 using namespace std; 6 const int maxn = 100000; 7 int sum[maxn<<2]; 8 void PushUP(int rt) { 9 sum[rt] = sum[rt<<1] + sum[rt<<1|1]; 10 } 11 void build(int left,int right,int rt) { 12 if (left == right) { 13 sum[rt] = 0;//我们干脆直接建一颗所有初始元素都是0的线段树 14 return ; 15 } 16 int mid = (left + right) >> 1; 17 build(lson); 18 build(rson); 19 PushUP(rt); 20 } 21 void update(int p,int add,int left,int right,int rt) //在p位置上增加add 22 { 23 if (left == right) { 24 sum[rt] += add; 25 return ; 26 } 27 int mid = (left + right) >> 1; 28 if (p <= mid) update(p , add , lson); 29 else update(p , add , rson); 30 PushUP(rt); 31 } 32 int query(int l,int r,int left,int right,int rt) { 33 if (l <= left && right <= r) { 34 return sum[rt]; 35 } 36 int mid = (left + right) >> 1; 37 int res = 0; 38 if (l <= mid) res += query(l , r , lson); 39 if (r > mid) res += query(l , r , rson); 40 return res; 41 } 42 int main() { 43 int m , n; 44 scanf("%d%d",&n,&m); 45 build(1 , n , 1); 46 char x; 47 while (m--) { 48 cin>>x; 49 int a , b , c; 50 51 if (x == 'y') { 52 scanf("%d%d",&a,&b); 53 printf("%d\n",query(a , b , 1 , n , 1)); 54 } 55 else { 56 scanf("%d%d",&a,&c); 57 update(a , c , 1 , n , 1); 58 } 59 } 60 return 0; 61 }
当然还有很多的线段树例题。但是我不建议用线段树去做luogu P1816 忠诚,那个题我觉得更适合ST表,因为是裸的RMQ,而且你线段树如果没有优化跑不快会被卡。
这里我讲的只是关于线段树很基本的一些东西,关于线段树,还有很多很多,比如二维线段树,重口味zkw线段树,各种各样的优化,不用递归建树等等等等......
希望对线段树初学者能有所帮助,如果我写的有不对的地方,希望大佬能指出。
最后推荐几个博客,也是对线段树的讲解:
http://blog.csdn.net/zearot/article/details/52280189
http://blog.csdn.net/zearot/article/details/48299459
http://blog.csdn.net/kzzhr/article/details/10813301
最后特别推荐_pks luogu 皎月半洒花的一篇对线段树的讲解
https://pks-loving.blog.luogu.org/senior-data-structure-qian-tan-xian-duan-shu-segment-tree
隐约雷鸣,阴霾天空,但盼风雨来,能留你在此。
隐约雷鸣,阴霾天空,即使天无雨,我亦留此地。


