ZR24 Summer A Day7 | Ad-hoc

CF1672E notepad.exe

询问的是宽度，而宽带范围太大我们无法直接枚举宽度找到最小行数。

于是暴力就是枚举所有可能的行数此时对应的 \(w\) 是在一个区间内的，二分一下 \(w\) 进行询问看看返回值是不是当前枚举的行，这样子的复杂度是 \(O(n\log n)\) 的。

观察数据规模大概是在 \(O(n+\log n)\) 级别的。

我们可以通过一次二分，找到全都放在第一行所需要的长度记为 \(w_1\)。我们枚举行数 \(h\)，发现放 \(h\) 行如果比 \(1\) 行更优的话，那么 \(h\) 的长度 \(w_h\le \lfloor\dfrac{w_1}{h} \rfloor\)。我们又知道放 \(h\) 行最多能节省的是单词之间的空格 \(h-1\) 个，即 \(h\times w_h\ge w_1-h+1\)，所以 \(w_h\) 只能取 \(\lfloor\dfrac{w_1}{h} \rfloor\)，对于每个 \(h\) 询问 \(\lfloor\dfrac{w_1}{h} \rfloor\)，如果返回值是 \(h\) 就去更新答案即可。

这个卡住上下界很精巧。

CF1354G Find a Gift

\(\mathrm{Trick:}\) 看到 \(> \dfrac{n}{2}\)，就要想到随机化。

可以发现石子的个数大于一半，且重量唯一最大，于是随机 \(\log n\) 个位置取重量最大的就几乎肯定是石子了。

现在我们得到了一个石子，要求出最前面的一个礼物。前缀长度最值可以考虑倍增。

每次询问一段长度为 \(2^{k-1}\) 的前缀，前 \(k\) 次询问了 \(\sum\limits_{i=0}^{k-1}2^{i}=2^{k}-1\) 长度的一个前缀，配合上我们第一次找到的石子点就可以得到一个 \(2^k\) 大小的集合。以此来询问第 \(k+1\) 次的 \(2^k\) 大小的集合。

在某一次中，我们发现了新增的集合重量小于之前的集合，于是就代表礼物在这个新增集合中，对于这个集合内部二分就行了。

QOJ7637. Exactly Three Neighbors

是否存在黑白相间的循环矩阵，满足黑格子占比为 \(\dfrac{p}{q}\)，且每个黑格子都与 \(3\) 黑 \(1\) 白相连。\(p,q\le 10\)。

数据范围很小，可以当作提交答案题来做。

先满这个约束条件，也就是颜色分布。我们可以构造三列，也就是两黑一白。由于是循环矩阵，这样子每个黑格子上下都有黑格子，左右是一黑一白。

可以发现 \(\le\dfrac{2}{3}\) 一定有解，因为上述构造是 \(\dfrac{2}{3}\)，因为对于白格子没有约束所以发现如果两个白列中间夹了一个白列这样子的话，白列是可以无限增多的。

同时分析上下界，\(1\) 白最多对应 \(4\) 黑，所以极限是 \(\dfrac{4}{5}\)。可以构造验证，用大小为 \(5\times 5\) 的矩阵，每列每行出现一个白即可。也就是用用一圈黑围一个白。

剩下就只有 \(\dfrac{3}{4}\)，\(\dfrac{5}{7}\)，\(\dfrac{7}{9}\)，\(\dfrac{7}{10}\)。

对于上述 \(\dfrac{4}{5}\) 的情况改造，如果我们用一圈黑围住两个白，那就是 \(\dfrac{3}{4}\) 了。

对于 \(\dfrac{5}{7}\) 和 \(\dfrac{7}{10}\) 都可以类似构造，但是 \(\dfrac{7}{9}\) 就很难办了。

对于 \(\dfrac{7}{9}\)，需要用多种图形强行拼接可以这么构造。

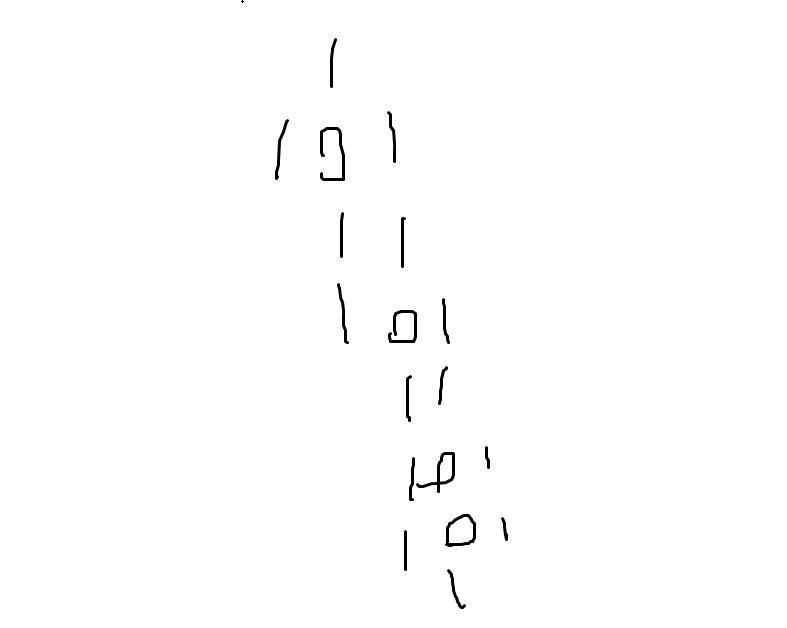
这样子可以构造出 \(\dfrac{2}{3}\) 到 \(\dfrac{4}{5}\) 间的所有数字。

HDU 7393

有 \(n\) 个人，每个人头上有个 \([1,m]\) 之间的某个数字，每个人都能看到其他所有人的数字，但看不到自己的。求一种整体策略，使得至少 \(\lfloor\dfrac{n}{m} \rfloor\) 个人猜对自己头上的数字。

发现一个人猜对的概率为 \(\dfrac{1}{m}\)，题目中所给下界就是近似于期望的一个数字。但是随机猜的话有可能低于下界，我们要构造一个互斥的方案。

互斥考虑分组，分成 \(m\) 组，使得某个组可以猜对，这样子就可以了。

不难发现如果我们知道了所有人的数字总和为 \(S\)，那么猜数字的人 \(i\) 可以立马知道 \(a_i=S-\sum\limits_{j\neq i} a_j\)。由于这个总和不确定，所以按照上述分组思想，我们可以对于总和分组，分成 \(m\) 组就是按照 \(S\bmod m\) 来分组，我们直接令 \(S\equiv i\pmod m\)，这样子就可以实现对于 \(n\) 个人每个人猜测的 \(S\) 的分组。于是第 \(i\) 个人猜测 \((i-\sum\limits_{j\neq i}a_j)\pmod m\)，由于是 \([1,m]\) 之间的数，所以我们 \(+1\) 即可。

AGC004F Namori

对于树有一个很巧妙的转化，就是按照深度奇偶性将点权颜色取反，这样子每次操作就可以看成交换相邻两个点的颜色。

CF1450C2 Errich-Tac-Toe (Hard Version)

对于 \(i+j\bmod 3\) 分三类，然后根据选哪两类又可以分成三种操作，这三种操作可以覆盖整个图，选最少的那个操作就行了。

Topcoder 13366

给定一个 \(n\times m\) 的图，其中一些位置是不能放兔子的，现在要求随机 \(r\) 个位置放兔子，然后每个兔子向欧几里得距离最近的兔子连无向边（如果有多个相同就行坐标最小，再相同就列坐标最小），问这样的图期望有多少个联通块。\(n,m\le 20\)。

把不可做通过找性质转化为可做。
每一个兔子连一条边，连出来的是一个基环树。基环树计数，可以对于环来计数。
我们发现一个圈上长度相同，同时又有长度相同的时候的坐标限制，所以只能是二元环。

CF1909H Parallel Swaps Sortf

把值域压成 0/1 可以做出 \(O(n\log n)\)，但是无法继续优化。

Zigzag MST

HDU 6664

给定无向图，有边权。求经过某 \(k\) 个点各一次的最大权值和。 \(n,m\le 10^4，k\le 6\)。
单次正确率 \(\dfrac{k!}{k^k}\)

AGC006D Median Pyramid Hard

削弱条件/特定数据
可以改成 \(a_i\in\{0,1\}\)。然后二分。

QOJ141. 8 染色

把两个优化拼接在一起。一种优化是只传前两个 bit 跑二分图染色，还有一个是度数优化。

CF1887E Good Colorings

考虑将行列拿出来形成一个二分图，中间连一条颜色边。\(2n\) 个点 \(2n\) 条边，必定有一个偶环。不断从中间缩短这个偶环即可。

AGC044D Guess the Password

\(dis(S,T)=\lvert S\rvert-\lvert T\rvert\)，当且仅当 \(T\) 是 \(S\) 的子串。

清华集训 文学

给定 \(p\le100\) 个平面上的点，和 \(n\le 100\) 个有代价的半平面（\(ax+by\le c\)），需要你选出一些半平面覆盖所有点，使得代价之和最小。

发现半平面剩下部分构成了凸包。区间 DP

HDU 6804

给定两个班级，分别有 \(n\) 和 \(m\) 个学生，学生有力量和价值两个属性，现在要对两个班级分别找出一个集合，使得这两个集合相等并且价值之和最大化。\(n,m\le 1000,w_i\le1000,\lvert v_i \rvert\le 10^9\)。

这个背包值域太大，于是打乱数组，期望值域是 \(O(\sqrt V)\) 的。

Pepe Racing

对于询问后凑不齐 \(n\) 个的就从别的里里面找一个非组内最大值的拉过来。这样子不会影响全局最大值。

AGC019F Yes or No

\(\max(n,m)\) 每次减一的时候，答案加一。不减的时候如果 \(n=m\) 答案加 \(0.5\)。