ZR24 Summer A Day2 | DS
P4719 【模板】动态 DP
详见 dp合集
这里就放个转移方程。
\(\begin{bmatrix}g_{i,0}&g_{i,0} \\g_{i,1}&-\infty \end{bmatrix}\)\(\begin{bmatrix}f_{j,0} \\f_{j,1} \end{bmatrix}=\) \(\begin{bmatrix} f_{i,0} \\f_{i,1} \end{bmatrix}\)
可以用树剖或者全局平衡二叉树维护。
lct 维护子树信息
对于每个点记录所有轻儿子信息和。把 \(u\) 转成根后,\(u\) 所在重链就是平衡树上右子树了。
在 access 中 \(ch(x,1)=y\) 的时候 \(O(1)\) 修改即可。
P8265 [Ynoi Easy Round 2020] TEST_63
发现本题这些操作有点像 LCT,于是我们考虑用 LCT 的虚实边来维护树上的轻重边。也就是对应映射一下。那么每个 Splay 上面维护的便是一条重链的信息。
考虑将 \(y\) 变成 \(rt\) 的操作,是先 \(\operatorname{access}\) 和 \(\operatorname{splay}\),再翻转。一次 \(\operatorname{access}\) 之后 \(y-rt\) 的所有边都变成了实边,对应一下也就是所有都变成了重边,但是显然不太符合实际情况。我们需要找到那些轻边在 LCT 中把他们变成虚边。因为根据轻边定义 \(sz_u > 2 sz_{son}\),所以对于每条轻边必然存在一个 \(k\) 使得 \(sz_u \ge 2^k > sz_{son}\)。可以枚举 \(k\) 通过 Splay 上二分找到 \(sz_u \ge 2^k > sz_{son}\),然后直接修。
对于统计重链第 \(k\) 大,在每次上述修改虚实边后一条重链会断成两段,我们将两段加入权值线段树中即可。
同时补充一下,对于上述 \(sz\) 的维护是在 LCT 中维护子树信息。做法是对于每个点记录所有轻儿子信息之和 \(gs\) ,改在 \(\operatorname{access}\) 中 \(ch(x,1)=y\) 的时候 \(O(1)\) 修改即可。子树大小就是 \(gs(u)+s(ch(u,1))+1\)。同时本题规定了在子树大小相同的时候,选择下接重链上编号更大的那个作为重儿子,于是我们还要记录最大编号。
然后有一个卡常小技巧就是用两个优先队列来代替 set,一个优先队列负责添加元素,一个优先队列负责删元素,这样子常数小了好多。
下面是对于 LCT 一些传统的函数内部细节的说明。
在 \(\operatorname{push}\) 中维护的信息 \(sz\) 信息不只是平衡树上信息了,还要加上其他轻儿子信息 \(gs\)。维护 \(val\) 代表实链异或和,也就是重链异或和。同时记录一下该重链中最大编号。
void pushup(int u){
s[u]=1+gs[u]+s[lc]+s[rc];
Mx[u]=max({Mx[lc],Mx[rc],u});
val[u]=val[lc]^val[rc]^u;
}
在 \(\operatorname{access}\) 中由于要修改 Splay 中右子树信息,这一项的修改涉及到了重链断裂成两个重链,同时新的重链生成。轻儿子的信息修改。于是我们记录下一路需要断开的边的位置,然后从上到下倒着修改一下。需要用到函数 modify(u,v)表示断开 \(u\) 原先的右子树,连上 \(v\)。首先,把原先保存的两条重链权值删掉。因为重链会发生变化。然后维护轻儿子信息,也就是轻儿子的子树信息和,还有 \(sz\) 的排名保存下来。然后在权值线段树中加入新产生的两条重链,注意第二条重链要在 \(\operatorname{pushup}\) 更新过新的重链信息后再加入权值线段树。当然对于 \(\operatorname{access}\) 造成的重链数量变多,我们在 \(\operatorname{link}\),\(\operatorname{cut}\) 和 \(\operatorname{makeroot}\) 这些调用 \(\operatorname{access}\) 的函数里面再修改,而不是立刻修改。
void modify(int u,int v){
seg.update(1,0,V,val[u],-1); if(v)
seg.update(1,0,V,val[v],-1);
if(rc) S[u].ins(s[rc],Mx[rc]);
if(v) S[u].del(s[v],Mx[v]);
gs[u]+=s[rc]; gs[u]-=s[v];
if(rc) seg.update(1,0,V,val[rc],1);
rc=v; pushup(u); seg.update(1,0,V,val[u],1);
}
然后 \(\operatorname{cut}\) 的时候,要注意我们先要根据子树大小看看谁是谁的父亲,然后本来要判断一下 \(v\) 是否是 \(u\) 的轻儿子,但是我们可以通过 access(u) 让 \(v\) 先变成 \(u\) 的轻儿子,这样子后面的操作就统一了。
\(\operatorname{link}\) 稍微修改一下,先记录一下轻儿子信息即可。
\(\operatorname{cut}\),\(\operatorname{link}\) 和 \(\operatorname{makeroot}\) 函数后面都要跟着一个 change
函数,就是上面那个枚举 \(k\) 然后 Splay 上二分修改轻儿子的操作。
其余未提及函数均按照原先写法即可。
JOISC2019D ふたつのアンテナ (Two Antennas)
很巧妙的一个线段树配合扫描线维护信息的题目。
发现 \(i,j\) 对称,不妨假设我们要求的是 \(i<j\)。
可以直接对于询问进行扫描线,扫 \(j\),线段树维护 \(i\) 位置处的答案。
在扫描线扫到 \(i+l_i\) 时标记 \(i\) 可用,在扫到 \(i+r_i+1\) 时标记为不可用。只需要在扫描线扫到对应位置的时候插入删除即可。
然后对于每个 \(j\) 在 \([j-r_j,j-l_j]\) 中为 \(i\) 的可能集合。于是我们用 \(a_j\) 在线段树上区间更新即可,线段树上维护 \(\lvert a_j-a_i\rvert\) 的最大值。
实现方法是我们在线段树上维护五个标记 \(mx,mn,tmx,tmn,A\) 前两个表示区间 \(a_i\) 的最大最小值,中间两个表示区间 \(a_j\) 的最大最小值,最后一个表示区间的答案。一定要注意 \(i,j\) 要分开来维护,不能混用。每次就用 \(mx-tmn\) 和 \(tmx-mn\) 来更新答案即可。
上面还提到了 \(a_i\) 的插入与删除,其实做法就是把单点修改 \(mx\gets 0\),\(mn\gets -\infty\)。
时间复杂度 \(O((n+m)\log n)\)。
P9061 [Ynoi2002] Optimal Ordered Problem Solver
首先有一个观察就有题中操作之后,我们可以发现被影响的点实时的位置形成了一条轮廓线。因此我们可以用二维偏序对于每个点找到第一个能够影响它的操作,这样子这就是它第一次进入轮廓线的时间,此后一直在线上。
可以用平衡时来维护轮廓线,因为轮廓线上的点满足 \(x\) 单调不减,\(y\) 单调不增,且不论怎么修改上面的点相对位置不变,于是我们以 \(x\) 为第一关键字,\(y\) 为第二关键字进行维护即可。询问和修改的都是一个矩形内的点,在轮廓线上对应的就是一段区间,因此用平衡树可以很方便的进行操作。
对于修改操作就是在预处理每个点加入轮廓线的时间,然后在对应时刻加入平衡树之中,同时对于已经在平衡树内的点可能会因为修改操作造成轮廓线形状的改变,直接对于一个区间进行 \(x/y\) 坐标的覆盖即可。
对于一个询问,能对其产生贡献的点分为在轮廓线上的点和不在上面的点。对于轮廓线上的点就是平衡树的一个区间和查询,对于不在轮廓线上的点就是 \((x,y)\) 二维偏序,不过为了辨别一个点是否在轮廓线上还需要用到进入轮廓线的时间 \(t\) 维度。于是 \((x,y,t)\) 就是三维偏序,时间复杂度 \(O(n\log^2 n)\)。
考虑优化一下,我们用总的点数减去不在询问范围内的点数。
如果询问点在轮廓线的话答案就是 \(0\) 了。如果在轮廓线外的话,我们根据询问点将不合法的空间划分成 \(3\) 个部分。对于 \(1,2\) 区域用 \((y,t)\) 二维偏序,对于 \(2,3\) 区域用 \((y,t)\) 二维偏序。\(2\) 区域算重了怎么办?容斥一下,减去 \((x,y)\) 二维偏序。对于 \(1,3\) 区域的轮廓线上的点用两次平衡树区间查询即可。
这样子拆成了若干个二维偏序,时间复杂度 \(O(n\log n)\)。

P8987 [北大集训 2021] 简单数据结构
两种思考方式,第一种是 xtq 上课的时候提出。
如果询问是在最后的话,可以考虑把所有 \(\min\) 操作移到最后。
考虑先 \(\min v\) 再 \(+i\),调换一下顺序就是先 \(+i\),再取 \(\min (v+i)\),最后就是若干个 \(\min (v+k\times i)\)。最终 \(a_i=\min(a_i+k\times i,\min\limits_j v_j+t_j\times i)\)。其中 \(t_j\) 表示 \(j\) 操作之后到末尾还有几次全局 \(+i\) 的操作。
考虑处理第二个 \(\min\),这是 \(a_i\) 的理论上界。这是一个在 \(t_j-v_j\) 的坐标系中的一个下凸壳用斜率为 \(-i\) 的直线来截取,可以发现随着 \(i\) 增大,\(\min v_j+t_j\times i\) 也是增大的,所以对于 \(i\) 更大的数的上界也是更大的,因此对于 \(a_i+k\times i\) 能达到上界的位置中数值是随着 \(i\) 单调递增的。可以发现这个结论对于任意时刻都满足。
于是考虑分成能某个时刻某个数否达到上界来考虑,对于当前时刻无法达到上界的位置直接线段树维护,对于当前时刻已经达到上界的数满足单调递增很容易,故可以用线段树二分完成 chkmin。于是对于每个数找到第一次达到界的 \(j\),此后这些数一直满足单调递增。因为一直符合性质,所以可以持续维护。
如何找到每个数第一次达到界的时刻呢,这个时刻是满足 \(a_i+k\times i\ge v_j\) 的,注意这里的 \(t_j=0\),因为我们以该时刻为截止时刻来考虑。移项之后就是 \(a_i\ge v_j-k\times i\),可以用整体二分配合李超线段树解决。时间复杂度 \(O(n\log^2 n)\)。
但我更倾向于题解区结合我个人想法的第二种思考方式,这个 chkmin 和 \(+i\) 都启发我们维护一个单调不降的序列。如果有这么一个序列经过 \(+i\) 之后还是单调的,chkmin 就是线段树二分之后直接打标记即可。
可以发现每次被 chkmin 影响的点此后都是单调递增的,因为这次 chkmin 抹平了他们之间的差距。此后 \(+i\) 后可以维持单调关系。
更进一步观察就是一些点如果先后被 chkmin,他们仍然保持单调关系。也就是说凡是被 chkmin 影响了至少一次的点都具有单调关系。考虑第一次被 chkmin 影响的点 \(i,k\) 和第二次被 chkmin 的点 \(j\),满足 \(i<j<k\)。第一次被 chkmin 之后肯定是 \(a_i=a_k>a_j\),如果最后一个不等号反向那么 \(a_j\) 也会被这次操作影响,矛盾,故式子成立。经历若干次 \(+i\) 操作之后是 \(a_i~?~a_j< a_k\),假设此时 \(j\) 也被 chkmin 影响了,那么首先 \(a_j=a_k\)。当 \(?\) 是 \(>\) 的时候,\(a_i=a_j=a_k\),当 \(?\) 是小于的时候 \(a_i\le a_j\le a_k\)。因此上述结论成立。
所以还是转化为求出每个点第一次被 chkmin 影响,同第一种方法解决即可。
QOJ8235.Top Cluster
给定一颗带点权的树,所有权值互不相同。多次查询距离一个点距离 \(\le d\) 的点的权值 \(\operatorname{mex}\)。\(n,q\le 2\times 10^5\)。
权值互不相同很重要,从这里入手。这代表对于每种权值只有一个代表点,想要在 mex 的时候值域连接上就必须包含住那个点。于是想要达到 \(V\) 就必须 \([0,V-1]\) 之内的所有点都到 \(u\) 的距离 \(\le d\)。转化一下就是其中的最远点到 \(u\) 的距离 \(\le d\),这提示了我们直径,于是考虑对于每种值域前缀都求一下直径端点然后 check 到端点的距离一下就行了。这个动态加点维护直径端点是很好做的,直接每次和原先 \(2\) 个端点共计 \(3\) 个点的三种距离找一下最远的距离就可以得到新的直径端点。
发现答案具有单调性,每次二分一下就可以做到 \(O(n\log n)\) 了。
DMOPC '21 Contest 8 P6 - Castle Building
给一个排列 \(a\),其中有些位置还未填入数字(用 \(0\) 表示)。每次会修改一个位置的信息,你需要每次判定能否补全排列,使得其满足 \(a_1<a_2<...<a_k>a_{k+1}>...>a_n\) 的形式。
\(n,q\le 2\times 10^5\)。
可以发现这个峰值位置很特殊,他一定是 \(n\)。同时应该是出现在单调性改变的位置,也就是在序列最大值的左边或者右边(或者 \(n\) 已经给出)的区间内,可以直接令它贴着最大值,这个不影响解的存在性。
枚举一下在左还是在右,然后每一个未填位置的区间就可以有一个值域范围。这是一个匹配问题,可以用 Hall 定理解决。由于连边形式是一个区间,所以 Hall 定理不需要对于集合 check 只需要对于区间 check,对于一个区间 \([l,r]\) 的判定我们又可以转化为去 check \(al+br>0\) 的形式。这样子就可以把二维转化成一维了,对于损失的一部分我们可以发现对于判定并不影响。对于每次修改只会修改 \(O(1)\) 个区间,很好维护。
P10145 [WC2024] 线段树
我连第一步转化都想不到,太妙了。
首先转化一下题意,对于区间 \([l,r)\) 我们在 \(l\) 和 \(r\) 之间连一条边,最后能表示出 \([L,R)\) 就是 \(L\) 和 \(R\) 联通。等价于去问,有多少边集使得给出的 \(m\) 对点联通。
先从特殊性质入手,就是整个图都联通。
我们可以对于线段树结构进行树上 dp,可以发现在线段树的 \([L,R)\) 节点上我们可以进行的操作是将 \([L,R)\) 连一条边,思考一下这对整张图联通性的贡献,当 \(L\to mid\to R\) 都有联通的时候这条边显然是没啥用的,但是当 \(L,R\) 没有通过 \(mid\) 相连的时候这是连接 \(L,R\) 唯一的机会,必须连上。当 \(L,R\) 都没有和 \(mid\) 相连的时候就不合法了,因为就算我们连接了边 \(L,R\) 也无法使得 \(mid\) 被联通,一旦有一个和 \(mid\) 联通,我们就可以通过形如 \(R\to L\to mid\) 的形式来达成整个的联通。
由上可以发现约束关系为儿子区间左右端点是否联通来决定该点是否进行连边操作,所以设 \(f_u\) 表示 \(u\) 子树内部合法,但是 \(L,R\) 不联通,\(g_u\) 表示 \(u\) 子树内部合法,但是 \(L,R\) 不联通。同时注意左右儿子中至少有一个 \(f\),否则 \(mid\) 无法联通。转移方程为
推广至非特殊性质,我们不需要全图联通而是需要刻画一个部分的联通性,所以需要研究一下局部联通的联通性。自己手画一些图可以发现这张图具有很强的包含性,就是这些区间都不是相交的,而是要么相离,要么包含的。那么一个区间内部的局部联通性就很好描述了,存在一个分解点 \(x\) 满足区间所有与 \(L\) 联通的点都在 \(x\) 左侧,所有与 \(R\) 联通的点都在 \(x\) 右侧。
可以利用这个特性进行 dp 统计。开两个数组,一个记录完全联通性,一个记录局部联通性。
设 \(dp_{u,i}\) 表示 \(u\) 节点下属区间的分界点为为 \(i\) 的方案数,\(f_u\) 表示 \(u\) 节点的 \(L,R\) 相连的方案数。
注意区别,之前 \(f\) 的定义是需要所有的都联通,现在的 \(f\) 只需要满足子树内部符合题目约束且 \(L,R\) 联通就行了,所以之前的 \(f\) 是不能通过两个儿子自己内部不连通的情况转移,而现在这个是可以的。
对于 \(f\) 的转移直接类似上面就行了,
最后一个转移单独列出,因为它比较特殊,需要满足 \([i+1,j]\) 内部无向外面的联通要求,这个可以用异或哈希来处理。
对于 \(dp\) 转移,
最后一类转移也是需要满足 \([i+1,j]\) 无向外联通的需求。
最后的答案就是 \(f_1+\sum dp_{1,i}\)
暴力 dp 是 \(O(n^2)\) 的。
发现对于第一类转移是 \(i\to i\) 自己贡献到自己,这启发我们用线段树合并维护 dp,只需要打一个乘法标记就行了。可是第二类转移不满足啊,考虑约束条件经过异或哈希处理之后是要求哈希值相等,于是我们直接用哈希当成下标就可以完成统一形式了。很巧妙。
时间复杂度 \(O(n\log n)\)。
P6109 [Ynoi2009] rprmq1
先考虑扫描线,扫 \(x\) 维度。矩阵加法可以用差分转化为两次区间加,然后对于矩阵 \(\max\),可以转化为执行时间 \([1,x_2]\) 内的操作,但是只统计时间 \([x_1,x_2]\) 内的区间历史最大值。
看到一段时间内的信息,可以用线段树分治来解决。但是这样子的话,由于每个询问会被分裂成 \(\log\) 个区间,所以最后 \(q\) 前面的系数会多一个 \(\log\),会造成对于 \(q\) 是 \(2\log\) 的。这样子会被卡常。于是我们采用猫树分治就可以去掉这个 \(\log\) 了。
由于是猫树分治,所以每一层内部使用扫描线,从左往右扫,对于加法操作,左加右减就行了。每次在询问右端点查询区间历史最大值,为了防止在不受到前面的影响,我们可以在进入左端点前给后面加上 \(\infty\),最后再减去即可。也可以打了一个标记,表示 \(his\gets mx\)。
时间复杂度 \(O(m\log^2n+q\log n)\)。
QOJ8240. Card Game
对于一个区间 \([l,r]\),其价值为维护一个栈从左往右将数压入栈中,如果当前即将加入栈中的数在栈中已经出现了就先执行弹栈直到那个数被弹出。强制在线,\(n,q\le 3\times 10^5\)。
设 \(t_i\) 为 \(i\) 后面第一次出现 \(a_i\) 的位置,记 \(\rm solve(l,r)\) 表示 \((l,r)\) 的答案。对于 \(l\) 进行从右往左扫描线,
\(\rm solve(l,r)=\begin{cases} \rm solve(l+1,r)+1 & r<t_l \\ \rm solve(t_l+1,r) & t_l\le r \end{cases} \)
使用主席树 \(+\) 标记永久化即可。
\(rt_i\) 中对于 \([i,t_l)\) 的部分直接继承 \(rt_{i+1}\),并且打上 \(+1\) 的标记。\(rt_i\) 中对于 \([t_l,n]\) 的部分是一段后缀继承,直接在最早被包含的点建立新点并且修改上方标记差带来的影响,下方儿子继承即可。
QOJ7884.Campus Partition
官方题解真的写的依托,dp 方程都很乱而且非常不严谨问题很大。
贪心一下,可以发现联通块其实就是幌子,取链的时候最优。而且只有最大值和次大值才会产生贡献,于是这两个一定是在端点处。以上约束条件就可以让我们很方便的 dp 了。
题目转化为选若干条不相交的链,每条链产生的贡献是两个端点取 \(\min\)。
设 \(f_{i,j}\) 表示以 \(i\) 为根的子树中,一端是 \(i\) 点,另一端为权值为 \(j\) 的点所以可以得到的除了这条链之外的最大代价之和,\(g_i\) 表示以 \(i\) 为根的子树的答案。
对于 \(f\) 的转移,我们枚举 \(u\) 的儿子 \(v\)。两种选择,一是从 \(v\) 向上延伸一条链(贡献为 \(f_{v,j}\))。二是 \(v\) 自己就独立了(贡献为 \(g_v\))。
那个 \(\sum g_v\) 最后加上就行了,于是就只需要对于 \(f_{k,i}-g_k\) 进行 chkmax 即可。
对于 \(g\) 的转移,首先是 \(g_u\gets \sum g_v\)。
然后就是需要将 \(f\) 在这个地方闭合。我们需要找到两个端点进行拼接在这里终结并且累加贡献,可以直接以 \(u\) 为一个端点。也可以将子树内的两个儿子拼接,贡献是 \(f_{v1,i}+f_{v2,j}-g_{v1}-g_{v2}+\min (i,j)\)。
对于这个较为复杂的转移,一个比较暴力的思路就是维护 \(v\) 作为 \(\min(i,j)\) 中的小者的贡献,\(pre_{u,i}\gets f_{v,i}-g_v+i\),再维护作为大者的贡献,\(suf_{u,i}\gets f_{v,i}-g_v\)。然后用 \(v\) 的信息和前面点的 \(pre,suf\) 匹配一下即可。
考虑优化,这里使用线段树合并来维护 dp。首先由于 \(\sum g_v\) 是最后加的,所以这个 \(suf\) 和 \(dp\) 的计算式子是一样的。只需要用两颗线段树维护 dp 值和 \(pre\) 就行了,对于它们在对应位置 chkmax,同时为了快速转移得到 \(g\),我们需要记录区间 \(\max\),每次左右两个区间拼接更新一下 \(g\)。
于是时间复杂度 \(O(n\log n)\)。
P11343 [KTSC 2023 R1] 出租车旅行
给定一颗 \(n\) 个节点的树,从 \(u\) 一步走到 \(v\) 的权值为 \(a_u\times dis(u,v)+b_u\)。求从 \(1\) 走到其他所有点所需的最小权值和。\(n\le 10^5\)。
注意本篇题解包括上述描述中的 \(a,b\) 数组和题面中的相反,读者自行 \(\rm {swap}\) 一下即可。
去年暑假集训遇到的题目,洛谷居然搬了。
感受一下这个过程,本来可以一步到位的,我们之所以选择一些途径点,可能是因为当前点的 \(a_u\) 太大了,我们需要走到一些 \(a_u\) 比较小的点上再出发(和 \(b_u\) 无关,因为从一个点出发,不管往哪里走都需要支付 \(b_u\))。于是可以得到一个结论,我们途径点的顺序必然是从 \(a_u\) 大的走到 \(a_u\) 小的点,当然最后的终点不一定满足这个条件。
于是考虑按照 \(a_u\) 从大到小加入每个点作为途径点的信息,对于每个点要从 \(a_u\) 大于它的点中求出到它的最小距离,也要把它加入后续点的选择中。直接做不好求,可以用点分治思想,如果经过 \(rt\),从 \(u\) 到 \(v\) 的代价就是 \(a_u\times d_v+(a_ud_u+b_u)\),这是一个一次函数可以用李超线段树维护。这启发我们建立点分树,每个点维护其子树内的一次函数,每次暴力跳父亲求其最短路,然后暴力跳父亲插入该点信息。
注意每次求完 \(dis(1,u)\) 之后,需要 \(b_u\gets dis(1,u)\),因为最短路需要类加上之前的路径之和。
上面插入的是途径点的信息,最后需要每个点作为终点再查询一下就行了。
时间复杂度 \(O(n\log^2 n)\)。
P8990 [北大集训 2021] 小明的树
trick: 联通块个数是 \(\lvert V\rvert-\lvert E\rvert\)。
题目要求等价于:未点亮部分不存在点亮的祖先,所以新的一个点被点亮后如果满足要求,那么未点亮部分为一个联通块,点亮部分联通块个数是 点-边。所以总体贡献就是 \(\sum\limits_{i=1}^{n-1}[未点亮的点-边=1](点亮的点-边)\)。
我们可以维护时刻 \(i\) 未点亮联通块的个数设为 \(c_i\),初始 \(n-1\) 条边未被点亮,时刻 \(i\) 后有 \(n-i\) 个未点亮,所以我们可以初始化 \(c_i=1-i\)。每条边都有一个被修改的时间也就是两个端点最被先点亮的时间 \(t\) ,然后对于 \(c_t...c_{n-1}\) 区间 \(+1\) 即可。
对于点亮的部分同理维护即可。初始有 \(0\) 条边被点亮,时刻 \(i\) 后有 \(i\) 个点被点亮,所以初始化 \(v_i=i\),记两个端点最晚被点亮的时候为 \(t\),对于 \(c_t...c_n\) 区间 \(-1\)。
如果在 \(c_i=1\) 的时候,统计答案呢?发现 \(c_i\) 的最小值就是 \(1\),于是我们只要维护区间 \(c\) 最小值,并且记录下对应 \(\sum v\)。
QOJ5017. 相等树链
看到路径统计问题考虑点分治。
我们对于 \(T_1\) 进行点分治,注意分治的时候我们不能遍历 \(T_2\) 中 \(T_1\) 的分治重心 \(u\) 的下方子树,因为 \(T_1\) 上平衡并不代表在 \(T_2\) 上是平衡的。
设当前分治重心为 \(c\),我们需要在 \(T_1\) 找到 \((u,c)\) 和 \((c,v)\) 组成的路径放到 \(T2\) 上判断是否成链。考虑在 \(c\to u\) 的过程中动态维护这条路径上所有点在 \(T_2\) 上形成的链的两个端点 \(p_1,p_2\)(如果不成链就直接返回了),这个通过一些对于 LCA 的分类讨论是很好维护的。在 \(c\to v\),的过程中也是同理维护端点 \(p_3,p_4\),最后需要 \(u\) 和 \(v\) 匹配,那么将两个点集内的点混合后如果在 \(T_2\) 上还成链其端点必然是 \(p_1,p_2,p_3,p_4\) 中的两个。根据端点组成类型分类,维护多个哈希值进行匹配。
上述确定端点的目的是为了得到整个路径的哈希值。
不过还是有一个问题,就是如果是 \((p_1,p_2)\) 或者 \((p_3,p_4)\) 成为最终的两个端点是不会出问题的,因为我们在遍历链 \(c-u\) 的时候保证了是两个端点,但是比如 \(p_1,p_3\) 组合,两条链得到的端点无法保证,当 \(T_2\) 上 \(c\) 到 \(p_1,p_2\) 路径上的第二个点相同时,此时不构成链但是哈希值有可能能匹配上这就不对了。于是我们需要对于上述情况按照 \(T_2\) 上 \(c\) 的相邻点分类再做一遍上述统计减去不合法的答案。如何找到某点是属于 \(c\) 的哪个相邻点下方的点?由于上面说了不能遍历 \(T_2\) 去打标记,我们可以用 dfs 序 \(+\) 二分实现。
如果用 std::map 会很慢,可以手写哈希表。
CF1558F Strange Sort
排序的最大次数就是最晚排好序的值所用的时间。于是考虑从局部思考,对于每个点独立求时间。
我们对于每个 \(x\in [1,n]\),设 \(\le x\) 的为 \(0\),\(>x\) 的为 \(1\)。我们得到了一个 01 序列,对这个序列进行题目中的排序,这个时间就是最后 \(x\) 复位的时间。我们对于所有 \(x\in[1,n]\),得到的答案取 \(\max\) 就是答案了。
对于某个 01 序列,我们设有 \(m\) 个 \(1\) 点,从左到右位置是 \(x_i\),到达时间为 \(t_i\)。
首先有,\(t_m=n-x_m+0/1\)(0/1 是奇偶修正)。
然后对于 \(i<m\) 的位置,首先路程是 \(n-(m-i)-x_i\),其次可能被 \(i+1\) 阻挡一下,如果被阻挡了就是 \(t_{i+1}+1\)。于是对于 \(\forall i<m\) 有,
以此类推即可。对于该 01 序列答案就是 \(t_1\)。
我们要对所有 \(x\) 求,那就是从大到小扫描一下值域每次讲阈值移动 \(1\),只有 \(1\) 个位置受到影响,很好动态维护。
令 \(d_i=n-(m-i)-x_i+0/1\),那么 \(t_1=\max\limits_{i}\{d_i+i-1\}\)。注意这里的 \(i\) 不是原排列下标,而是在值为 \(1\) 的序列中的相对位置。
考虑使用线段树维护 \(\{d_i+i-1\}\) 序列,线段树下标是原排列中的位置,但是 \(i\) 指的是 \(1\) 序列中的位置。每次移动阈值 \(x+1\to x\) 的时候,\(x\) 变成了 \(1\),于是加入该点信息。此时 \(m\) 变大了 \(1\),对于右侧点它们的编号也增加了 \(1\)。于是对于右侧点需要区间 \(+1\),对于左侧点要区间 \(-1\)。
需要特判一下,如果末尾一段连续的 \(1\) 的时候这些已经不需要移动了,也就是说这一段答案为 \(0\),然而奇偶修正可能导致其为 \(1\)。所以直接设置为 \(-\infty\) 即可。
时间复杂度 \(O(n\log n)\)。
QOJ4815. Flower's Land
给定 \(n\) 个点的一棵树带权。对于每个点求包含它的大小为 \(k\) 的联通块的最大权值。\(n\le 4\times 10^4,k\le 3\times 10^3\)。
先看一个弱化版,求全局最大的联通块。
首先是一个技巧 dfs 序背包的 trick,设 \(f_{i,j}\) 表示 dfs 序在 \([i,n]\) 之内的点选 \(j\) 个点构成的背包。由于是要求联通块所以要么选儿子要么整个子树都不选。
于是就有,\(f_{i,j}=\max(f_{i+1,j-1}+a_i,f_{i+sz_i,j})\)。时间复杂度 \(O(nk)\)。
由于是对于每个点都要求,考虑点分治。每次对于分治中心 \(rt\) 旗下所有点 \(u\),求出同时包含 \(u,rt\) 的联通块的最大权值。
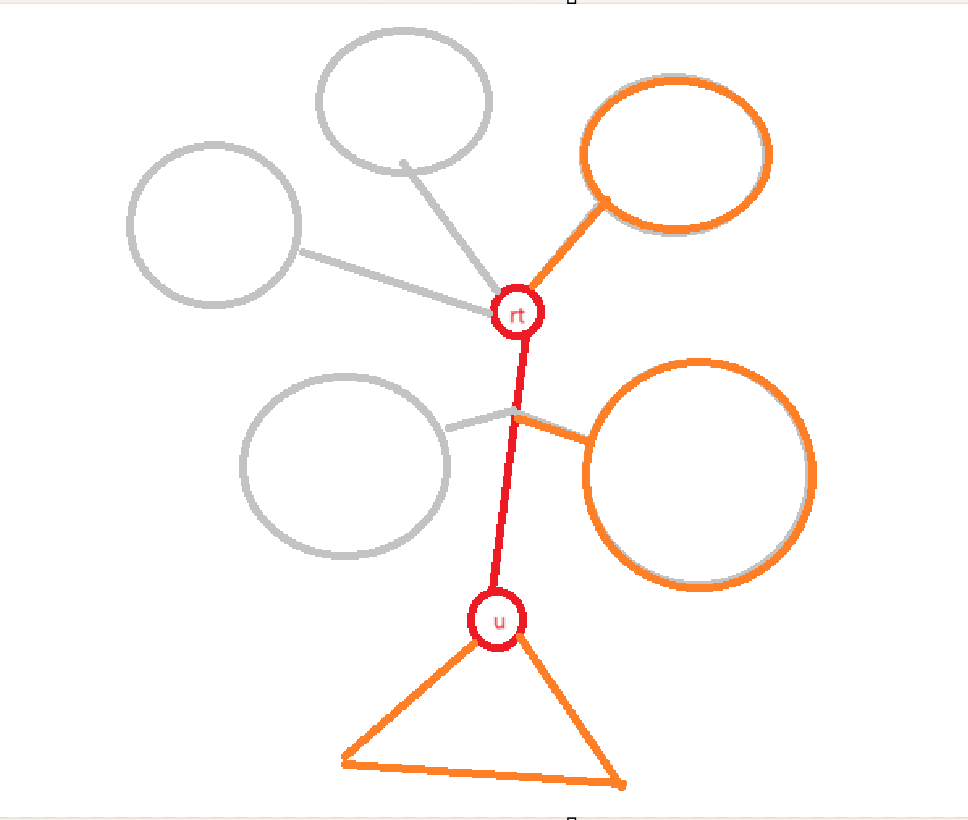
分析一下要选哪些点,首先 \(u-rt\) 路径上的所有点必选(红笔标出)。
然后将点分成两类,dfs 序在 \(u\) 前面的(银+红),dfs 序在 \(u\) 后面的(橙色,其中三角形代表 \(u\) 的子树)。
对于第二类点,直接对于 dfs 序 \(> dfn_u\) 的点做一遍背包即可。
对于第一类点其实不好处理,因为其包含了银色(我们需要加入的贡献)和红色(强制要求加入的贡献),红色 dfs 序混入了银色之中很难分离。这里有一个很巧妙的做法,我们将原本遍历儿子的顺序颠倒(代码实现就是 reverse 一下 std::vector 数组 \(G\) ),这个时候加入 dfs 序 \(\ge dfn_u+sz_u\) 的点的贡献即可,因为这个时候红色会和橙色混合在 dfs 序 \(<dfn_u\) 的部分,而灰色正好被分离出来了。
剪枝一下,分治联通块大小不足 \(k\) 肯定不优,直接 skip。时间复杂度 \(O(nk\log{\frac{n}{k}})\)。
看了一下官方题解,还有一个更优秀的做法。
设 \(f_{u,i}\) 表示 \(u\) 子树内选择 \(i\) 个点可以得到的最大权值。为了求出最后答案,肯定是需要和 \(u\) 之外的一个部分进行合并,所以我们设 \(g_{u,i}\) 表示 \(u\) 上方的一个联通块内选 \(i\) 个点可以得到的最大权值。我们在 \(u\to v\) 的时候求解 \(g_v\),可以发现其实就相当于在 \(g_u\) 的基础上加入 \(u\) 点,加入 \(v\) 的兄弟子树。关于加入兄弟节点,可以对于 \(u\) 的所有儿子进行一个前缀背包和后缀背包,再把 \(pre_{v-1}\) 和 \(suf_{v+1}\) 拼接在一起就可以恰好扣掉 \(v\) 子树信息。时间复杂度 \(O(nk)\)。
这里要注意一下细节,暴力卷积是 \(O(k^2)\) 的,我们必须把求 \(pre,suf,g\) 的卷积做成类似树形 dp 的转移枚举。对于 \(pre\) 的求解很简单就类似于求解 \(f\) 一样动态更新 \(sz\) 卡住上界。对于 \(pre\times suf\to g\) 的卷积需要注意卷积出来的数组大小必须 \(\ge k-sz_v\) 否则没意义,这个下界优化也可以将大小枚举形式规约到树形 dp 的枚举形式上。但是 \(pre\) 的求解就需要小心了,因为我们上述说了还要带上 \(g_u\),为了方便直接设 \(pre_0=g_u\),往后卷,但是如果直接做复杂度还是不对,因为这个形式不符合树形 dp 一个一个合并子树了,而是直接就有了一个 \(sz(g_u)\) 的基础了,一条链就可以卡爆。其实 \(pre\) 有用的部分只有 \([k-sz_{suf},k]\) 这么多,因为更小的就凑不出来 \(k\) 了,所以还是可以转化到树形 dp 复杂度上。
Segbeats
维护一个支持以下两种操作的数据结构
- 区间 chkmin
- 区间和
使用线段树,维护区间最大值,严格次大值,最大值的个数,区间和。
如果 \(c>mx_1\),就直接返回。
如果 \(mx_1>c>mx_2\),我们就把所有最大值变为 \(c\),且修改区间和 \(sum\gets num(c-max1)\)。
如果 \(c\le mx_2\),暴力递归。
时间复杂度 \(O(n\log n)\)。可以有单点修改,如果有区间加,是 \(2\log\)。常数很大。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号