构造/交互/Ad-hoc专题
P6663 [POI 2019] Układ scalony
首先,构造上下界。上界显然是 \(nm-1\),下界需要分奇偶讨论。
右下左上联通,所以需要至少 \(n-1+m-1\) 的长度,我们发现对于 \(m,n\) 中有一个奇数的情况是可以满足的。在奇数那里从中间一列劈开,然后分别向两边连。对于偶数,我们无法到最中间的那个,那么只能选择相对更靠中间的那个。但是如果我们这么选
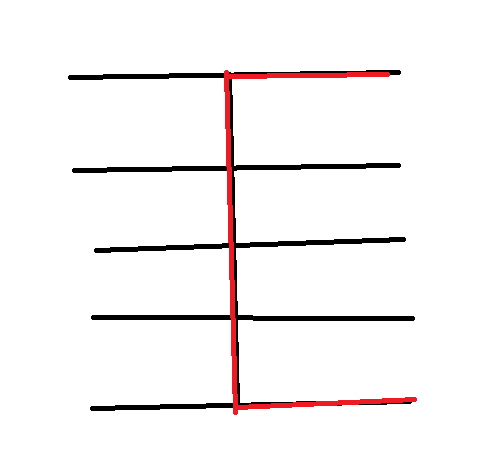
会造成长度加一,也就是 \(n+m-1\)。
最后的构造很显然就是调整法了。我们逐步将最小情况往大去调整,直到遇到答案。以 \(n\) 为奇数为例,我们先构造出红笔的主链,然后目前潜在的连边方式是黑笔的下界,如果我们要调整就一点一点地调整成蓝笔的上界,按照那个螺旋线一点点走就行。
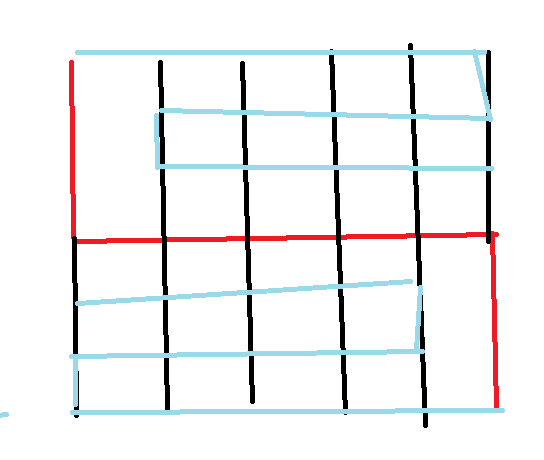
我们可以设置一个标号数组,\(f_{i,j}\) 表示该点连边的朝向,初始化就初始黑边朝向即可。然后如果要变更,就改成蓝笔朝向。
本题在 \(n,m\) 为偶数的时候的构造,初始状态不要设置为图 \(1\) 中那种最小值情况,而是同理设置为图 \(2\),方便后续调整构造,图 \(1\) 形态不方便调整。
P9837 汪了个汪
由于题目要求二元组不同,于是思考二元组特征。
发现一共要填 \(\dfrac{n(n+1)}{2}\) 个二元组,而二元组的个数恰好也是 \(\dfrac{n(n+1)}{2}\),于是就是要根据二元组特征给全体二元组分类。且最好每一类的个数分别是 \(1,2...n\) 这样子正好对应每一行。可以根据二元组两个数之差来分类,这样子正好满足上述条件。
但是我们无法这么去安排数字,下面是一个小技巧,如果可以(相同数字代表一类)
这么放,那么我们同样可以
于是我们可以按照 \(x~x+1~x-1~x+2~x-2...\) 这么来放。最后根据长度排序即可。
本题还可以在半圆上使用 Zig-Zag 来解决。有时间的话就更一下。
CF1325C Ehab and Path-etic MEXs
首先特殊情况,链,随便填。
其他情况的几种思考方式
-
可以自己试几组或者打表,发现答案均为 \(2\) ,于是往 \(2\) 上面构造。
-
根据 \(\rm mex\) 性质考虑分离几个最小值,因为一条链上的一个点对这条链最多有两条边的贡献,所以取前三小值 \(0,1,2\) 放在一个点的三条出边上。
我自己的想法是考虑到要求的是 \(mex\) 的最大值以及 \(mex\) 的性质,于是可以想到一条叶子到叶子的路径比其他路径更可能对答案产生贡献。(好像对本题没啥用)
P7915 [CSP-S 2021] 回文
这题的构造策略是先选取序列的第一个(最后一个同理)加入 \(b\) 中,发现与 \(a_1\) 相同的那个 \(a_x\) 必须最后放入序列中。
于是可以在 \(a\) 数组中以 \(a_x\) 为分界点,此时切记不可再考虑选取 \(a_2\) 或者 \(a_{2n}\) 再次选取分界点。而是应该根据 \(a_x\) 为最后一个推导出 \(a_{x-1}\)或者 \(a_{x+1}\) 为潜在的倒数第二个,于是在序列两端寻找能否找到与 \(a_{x-1}\) 或者 \(a_{x+1}\) 相同的数作为 \(b_2\) 。以此类推,即可完成构造。
ARC144C K Derangement
构造可行解,在条件允许范围内微调使得更优。判断一下如果该数往前放的话,目前的位置可以有其他数字填补就可以进行操作。
CF1311E Construct the Binary Tree
很显然的就是先构造出一组极限情况,然后不断调整。这里以先构造一棵满二叉树为例。构造出以后,感觉自己思路还是有点乱,想的有点放开了,以为是一堆点移来移去,这样子显然是很完成构造题的。还是要大胆猜想出一个一般性策略然后实现。由于极限情况是一条链,所以我们可以把目标设置为链形。首先维护一条链,然后不断把树上节点挂上去。如果 \(rest_d\) 突然小于 \(0\),说明目前链长大于 \(-rest_d-dep_i\),故一定可以在链上找到一点使得 \(rest_d =0\) 并且该点没有挂上子节点,往上放就可以了。
CF1916F Group Division
考虑动态构造这个集合,每次选取剩余图上的与选取图联通的非割点加入即可。
如果要严谨点,可以证明一下存在性。
CF1736D Equal Binary Subsequences
首先 \(0~1\) 个数不相等肯定不行,我们可以大胆猜测一下个数相等的时候必然可以。其实我们也可以发现满足情况的可能很多,所以可能并不能直接找到一个通法。但这也说明了操作空间很大,我们可以钦定一种方案,强行构造。肯定选择相对便利的方案尝试构造,如果两组中对应位置在 \(s\) 中差距过大,那么难以操作,于是我们可以采取一些方法使得两组中对应位置相邻。效果就是类似 \(0011001111110000\) 。考虑分组,\((i,i+1)\),当 \(s_i=s_{i+1}\) 显然可以,我们将不相等的位置提取出来,必定形如 \((1,0)~(0,1)\) 交替着选出 \(0~1\) 然后平移即可。
CF1521E Nastia and a Beautiful Matrix
构造最小矩阵,一般要考虑答案下界,我们发现在 \((2x,2y)\) 的位置填入 \(0\) 剩下的位置填入 \(0\) 这样子显然是最大化的。此时可以填入 \(n^2-\lfloor \frac{n}{2}\rfloor^2\) 个数。设出现次数最多的数出现了 \(Max\) 次。那么为了实现要求 \(2\),需要满足 \(n\lfloor \frac{n}{2}\rfloor \ge Max\),于是二分出最小的边长同时满足两个条件即可。这只是必要条件,为了使得结论充要,下面我们需要给出一个满足条件的构造。条件一是已经满足的了,条件二需要我们让相同数字尽可能在同一行或者隔 \(2\) 行及以上,而非相邻行。直接对于 \(a_i\) 排序,把 \(a_i\) 个 \(i\) 依次放到一个序列中。按照序列顺序放到所有 \((2x+1,y)\) 上,放完之后再放 \((2x+1,2y+1)\) 这显然是更可能的去贴合条件二的情况。下证这构造满足条件二,发现对角线的两个数在序列中位置相差 \(\ge n\lfloor \frac{n}{2}\rfloor\),由上述二分可知,没有某个数出现次数大于 \(\ge n\lfloor \frac{n}{2}\rfloor\) 因此得证。
CF1365G Secure Password
首先可以转化一下题意:每次可以询问一个集合,要求最后对于每一个 \(i\) 需满足询问的集合中不含 \(i\) 的集合的并集等于全集去掉 \(i\)。
其实就是一个集合划分问题,再进一步转化一个上面的条件也就是对任意 \((i,j)\) 满足 \(j\) 出现在一个不含 \(i\) 的集合中。于是我们可以通过元素特征来划分集合。\(i\) 和 \(j\) 不同当且仅当二者的二进制表示中有一位不同,这启发我们考虑二进制的每一位分别询问下标的当前位为 \(0\) 和 \(1\) 的元素的集合。但是这样操作次数是 \(20\) 次。
如何减少操作次数呢,发现操作次数是等于集合总数的,于是我们可以通过减少集合总数来削减操作次数。在当前的划分方式下 \(20\) 个集合确实是必要的,因为只有这样才能区分出那些只有一位不同的数,所以我们可以选择更具有特征性的划分方式。
我们发如果固定 \(1\) 的个数这样不需要对于每一位正反查了,因为如果当前位 \(i\) 为 \(0\) 而 \(j\) 为 \(1\),那么必然存在另一位使得 \(i\) 为 \(1\) 而 \(j\) 为 \(0\),只需要在 \(1\) 的位置统计就可以了,这样就不需要正反询问了。
为什么询问次数上限是 \(13\) 呢,因为 \(C_{12}^i \le C_{12}^6 <1000\),而 \(13\) 恰好满足条件。
P9721 [EC Final 2022] Inversion
区间逆序对显然是不好得出什么结论的,于是我们考虑将区间逆序对转化为有用的东西。
这里一定要敢想,交互题一开始的思路就是先能做出来,再考虑次数限制。所以我们不要吝啬操作次数。我们发现可以用 \(4\) 次询问容斥原理得出 \(a_l\) 与 \(a_r\) 的相对大小关系。
得到的关系只是相对关系,这启发我们动态地维护相对大小,最后就可以得到总的序列。
设 \(pos_i\) 为目前相对排名为 \(i\) 的数的位置,\(a_i\) 表示 \(i\) 位置目前的相对排名。
每次新加入一个 \(p_i\),我们要求出 \(a_i\) 也就是 \(p_i\) 的相对排名。可以二分一下排名就行了,用所给函数来比大小。最后还需要来考虑一下次数。
第一个优化是记忆化。第二个优化发现对于 \(i\) 的每个询问要用到两次 \(f(k,i-1)\),我们很可能要调用函数计算,但其实不用,因为我们已经得出了前 \(i-1\) 个数的相对大小,所以可以直接判断。故其实一次询问只需要调用两次函数。
P3641 [APIO2016] 最大差分
\(T=1\), 的时候我们直接询问 \((0,10^{18})\) 便可以得出最大最小数,然后把最大最小数往中间缩一就可以得到次大和次小,以此类推得到整个数列。
\(T=2\),次数约束的是区间内数的个数,我们发现区间内数的个数越多,答案应该是越小的,而我们要求的是最大化答案,所以两者之中存在一个平衡。这里我们取 \(B\) 为答案下界,\(B=\frac{a_n-a_1}{n-1}\),每次跳跃着查询即可。答案只会是上一个块的最大值和当前块的最小值之差。考虑 \(M\) 是否符合要求,第一次 \(M \gets n+1\),后面会询问 \(n-1\) 次,总共覆盖到 \(n-2\) 个数,于是 \(M \gets n-1+n-2\),所以总数是 \(3n-2\)。
CF1158C Permutation recovery
一眼线段树建图+拓扑排序。不过还有更简便的方法。不过仔细考虑一下就是需要满足 \(i \to p_i\) 不相交就行了,于是单调栈判断一下就行了。考虑 \(-1\) 如何处理,我们发现 \(i\) 和 \(p_i\) 越近越容易满足条件于是直接设为 \(i+1\) 即可。然后需要构造,我们肯定是先构造出约束条件最少的,所以直接按照 \(p_i\) 降序,\(i\) 升序把 \(n-1\) 填入即可。
CF1354G Find a Gift
基本想法肯定是找出一些石子做参考物,然后比较。
问题是我们很难找到很多石子,但是发现石子的个数大于一半,且重量唯一最大,于是随机 \(\log n\) 个位置取重量最大的就大概率是石子了。现在我们得到了一个石子,显然是不够支持我们做大规模询问的,我们单组询问的规模是和已知石子的个数相等的,这里可以倍增,如果目前询问的一组里面没礼物,那么就必然全是石子且可以供我们所用。
CF1493F Enchanted Matrix
发现行列独立,可以分开处理。只需要在 \(n\) 或者 \(m\) 的约数中寻找。对于任意 \(r\),如何判断合法性呢,根据 border 结论,只需要比较 \((1,n-r)\) 与 \((r+1,n)\) 即可。但是本题要求不重叠,我们不能这么问。拆分一下即可,\((1,mid)~(mid+1,2*mid)\) \((1,mid)~(mid+r+1,2*mid+r)\)
CF1514E Baby Ehab's Hyper Apartment
看到竞赛图联通性,肯定要去想 tarjan 缩点之后竞赛图是一条链这个关键结论。但是如何利用这个结论?
第一想法肯定是动态维护这条链,然后通过二分等手段定位其所有在的 SCC,往里面加点。
发现单点和 SCC 进行 check 二者关系是一件困难的事情,因为我们需要 check 双向联通性,但是询问一只能得到是否存在某条边的信息,这就很不利于我们的判定的,最坏情况下要遍历整个 SCC 才能知道二者关系,操作次数无法接受。
但是我们有操作二,可这仅仅能得到点 $\to $ 集合,无法得到集合 \(\to\) 点,不能进行双向串联。
所以第一个想法落空了,于是考虑先得到一个弱化版信息,我们可以充分利用得到边信息这个手段,这是竞赛图存在哈密顿路径,所以可以通过二分询问边信息来找到一条哈密顿路径。我们二分联通性,然后在当前序列中间插入点。另一种很好的做法是可以直接把题目给的操作一的交互接口看成 std::stable_sort 的 cmp 函数,对其进行排序,最后得到的序列也是某条哈密顿回路。次数 \(O(n\log n)\)。
找到这条路径之后,我们要把这条路径的若干个区间缩起来得到 SCC,缩 SCC 等价于找到这条链上的反向往回走的边。问题又来了,我们还是只能得到连边信息,不能直接得到联通性信息,所以不能询问相邻两个 SCC,而且是应该去询问一个前缀 SCC。
我们倒序枚举这条哈密顿路径上的点,通过操作二查询,如果 \(i\to \{1,2,3\dots i-1\}\),那么就可以把 \(i\) 所在 SCC 和 \(i-1\) 这个点缩在一起。次数 \(2n\)。
CF650E Clockwork Bomb
初始树为 \(T1\),目标树为 \(T2\)。
考虑一下下界显然就是在 \(T1\) 在 \(T2\) 中没有出现的边的数量。
但是我们需要满足每次操作完仍然是一颗树。我们发现某个节点只要向上连边就必然保持树的形态,如果向下连边就会出现环。于是我们从叶子节点开始向上遍历即可。
注意处理特殊情况,\(T1\) 和 \(T2\) 中父子颠倒。如果在 \(T1\) 中 \(u\) 为 \(v\) 父亲,可是在 \(T2\) 中 \(v\) 为 \(u\) 父亲,那么我们要保留边 \((u,v)\),可以在从下往上遍历到 \(v\) 的时候,如果 \(v\) 要连自己在 \(T2\) 中的父亲的话,就要断开 \(T1\) 中的边 \((u,v)\) 否则可能成环。矛盾。
于是我们将断开 \(T1\) 中的 \((u,v)\),改为断开 \(T1\) 中 \((fa_u,u)\),这样既保留了边 \((u,v)\),又保证不会成环。可是同理如果 \(T1\) 中的 \((fa_u,u)\) 在 \(T2\) 中也出现过怎么办呢,我们可以采用并查集,找到该链上第一个不同时出现的边断掉即可。
P3514 [POI2011] LIZ-Lollipop
看到这题我的第一反应是每次 \(+-1\) 造成值域连续性,本题中如果是 \(0 1\) 序列的话值域也是连续的。可是这里有一个 \(+2\),按照前面的思路来想,可以发现这里是 \(2-\) 连续的。
假设 \([l,r]\) 和为 \(x\),如果两个端点是 \(1\),我们可以同时拖动两个端点使得其变成 \(x-2\),如果两个端点中出现一个 \(2\),我们也可以减去它构造出 \(x-2\)。
CF468C Hack it!
我们发现单独的各位数字累加没有什么规律或者好用的性质。
于是可以思考两两配对。就是令 \(p=\sum\limits_{i=1}^{10^{18}}i \bmod a\),然后把上界 \(+1\),下届 \(+1\),就可以发现增量就是 \(1+18 \times 0=1\),一直增加直到满足要求即可。
P7115 [NOIP2020] 移球游戏
先思考 \(n=2\) 时候的解法,记录两个栈为 \(s_1\) 和 \(s_2\),分别目标为 \(1\) 球和 \(2\) 球。我们现在想要其中一个栈变成全 \(1\)。我们发现 \(s_1\) 和 \(s_2\) 都往空栈里面放一点东西进去似乎只有暴搜放进去的顺序然后 \(2\) 和 \(3\) 栈互相搞一下的很暴力的做法,没有可扩展性。有没有什么好办法去分离 \(1\) 和 \(2\) 两种小球呢,只有两个空栈能办到。我们现在只有一个空栈,转念一想,其实我们可以再创造半个空栈,设 \(s1\) 中有 \(a\) 个 \(1\),那么我们只需要从 \(s_2\) 中挪 \(\min(a,m-a)\) 个球给 \(s_2\),然后将 \(s_1\) 中球依次弹出,分别放到 \(2\) 和 \(3\) 中这就实现了分离。
那么对于 \(n>2\) 的时候呢?把问题转化到 \(n=2\)!直接设置一个阀值 \(x\),然后 \(\operatorname{solve}(l,r)\),把 \((l,r)\) 分成两半,两边两两匹配,然后大的到一边小的到一边就行了。
还有一种解法是按照 \(n=2\) 的相同手法对于双栈进行排序,使得 \(\max s_1 \le \min s_2\),然后对于所有栈归并排序一下就行了。
P8150 再会 | Sayounara
可以发现由于交互库只能返回 \(\sum a_i-\min a_i\) 的结果,最小值被减去了。所以对于区间 \([l,r]\) 其最小值是一个隐藏信息,不管再怎么用区间内的数去组合询问,都无法得到最小值。
将上述思想扩展至全局,全局最小值更是不可能由操作一得到。所以我们的有一次询问操作二的机会肯定是留给全局最小值的。同时可以发现,一旦我们得到了全局最小值就一定可以在 \(n-1\) 次操作一之后还原整个数组。
所以现在的任务就是用 \(301\) 次操作一和 \(1\) 次操作二确定序列最小值的位置。
试了很久之后,想起来 P9721 [EC Final 2022] Inversion,那一题中是通过 \((l,r),(l,r+1),(l-1,r),(l-1,r+1)\) 四个区间的返回值异或在一起得到两个端点的大小关系,这启发我们不一定是要独立地分析每个询问的返回值,可以考虑将询问的返回值通过运算组合在一起。可以通过类似差分/减法运算使得某个信息暴露出来。
于是我们考虑试一下 \(query(l-1,r)-query(l,r+1)\),看看能否得到 \(a_{l-1}\) 和 \(a_{r+1}\) 的大小关系。
设 \((l-1,r)\) 和 \((l,r+1)\) 的最小值分别为 \(p,q\)。如果两者返回值相等,根据元素互不相等,可以得到 \(a_{l-1}=p\),\(a_{r+1}=q\)。如果前者返回值大,可以得出 \(p=q\),\(a_{l-1}>a_{r+1}\)。
我们可以惊奇地发现我们基本得到了 \(a_{l-1}\) 和 \(a_{r+1}\) 的大小关系,虽然在有的情况不能准确得出。同时可以得到一个更有用的情况,也就是最小值的分布位置。第一种情况可以得到最小值在两个端点,第二种情况可以得到最小值在 \([l,r]\)。这启发我们不断缩小可能区间来得到最后的最小值位置。
所以我们可以 \(\operatorname{solve(l,r)}\) 来找到 \([l,r]\) 的最小值,我们把序列平均分为三段,\([l,s],[s+1,t],[t+1,r]\)。然后比较
列式子分析一下,记录中间区间的和为 \(sum\),三个区间的最小值分别为 \(m_1,m_2,m_3\)。
-
\(m_1\) 为区间最小值,那么 \(L=s\),\(R=s+m_3-\min(m_2,m_3)\),故此时 \(L\le R\)。
-
\(m_2\) 为区间最小值,那么 \(L=s-m_2+m_1\),\(R=s-m_2+m_3\),故此时 \(L\neq R\)。
-
\(m_3\) 为区间最小值,同理分析可得 \(L\ge R\)。
我们每次根据 \(L,R\) 的大小关系可以舍弃一个区间。当 \(L=R\) 的时候,我们舍弃中间区间。当 \(L<R\) 的时候我们舍去最右边区间。当 \(L>R\) 的时候,我们舍弃最左边区间。
因为存在舍弃中间区间的可能,这样子可能会造成序列不连续,但是经过讨论可以发现,中间区间如果在上一步被舍弃,代表最小值不在其中,那么后面的询问带上这个区间也不会造成影响。
如果区间长度等于 \(2\),可以用一次操作一和一次操作二来解决。
需要的操作 \(1\) 次数大概是 \(4\log_{\frac{3}{2}}10^6=136\) 次,符合题目要求。
AGC030C Coloring Torus
对于题目要求很神秘的题,我们可以尝试从感性角度理解一下题目,其实题目的要求就是对于每个数字相同的格子,要求他们所处的 "地位相同"(周围数字的可重集合相同)。所以相同数字的格子应该是比较对称的。
所以我们可以给出 \(k\le 500\) 的构造,就是第 \(i\) 行全填 \(i\)。
对于 \(k> 500\) 的情况,我们无法采取以上策略,因为会有若干数学无法填入了。
思考一下能否扩展,在 \(4\mid n\) 的时候,我们将更大的数间隔塞入。
1 5 1 5
2 6 2 6
3 7 3 7
4 8 4 8
对于 \(4\mid k\) 的情况,我们还是可以构造出来这么一个对称形状的。
对于 \(2\mid k,4 \nmid k\) 的情况,同一行内首尾相同会造成不满足要求。
同时当 \(k\) 是奇数,我们也无法完成。因为必然存在某一行无法被更大数间隔地塞入。局部结构大概是这样子地,
1 x 1 x
2 2 2 2
我们可以发现偶数列的 \(2\) 可以被 \(x\) 影响到,但是奇数列的 \(2\) 无法被 \(x\) 影响到。所以 \(2\) 的地位不对称。
考虑如何解决这个问题,我们要通过某种手段使得统一奇偶列。可以发现如果我们将原图旋转 \(45°\) 的话,原本和 \(x\) 在对角线的奇数列 \(2\) 就可以和 \(x\) 相邻了,并且偶数列的 \(2\) 还是保持相邻。而且对角线也正好保证了对称性。
先给出对角线的基本 \(k\le 500\) 构造。
当 \(k=6\) 的时候,大概是长这样子的,
1 2 3 4 5 6
2 3 4 5 6 1
3 4 5 6 1 2
4 5 1 6 2 3
5 6 1 2 3 4
6 1 2 3 4 5
尝试加入三个数,我们就按照对角线上交替放的原则来插入新数。
1 2 3 4 8 6
2 3 9 5 7 1
3 4 8 6 1 2
9 5 7 1 2 3
8 6 1 2 3 4
7 1 2 3 9 5
注意就是我们默认上三角矩阵加入新的数字就是从每个斜线的第一列开始加,然后对于下三角矩阵,为了符合要求,对于第 \(i\) 行,我们从 \(1+(i\bmod 2)\) 列开始加。
可以发现是符合要求的。发现只有 \(n\) 为偶数的时候,构造才符合要求,因此取 \(n=\lceil\frac{k}{4}\rceil\times 2\)。我们维护 \(2n-1\) 条对角线,然后不断插入新的数,最后还原成一个正方形即可。
其实还有一种构造很精妙,那就是 \(k\le 500\) 的时候 \(a_{i,j}=(i+j)\bmod n\)。对于 \(k\) 更大的情况进行调整。这样子保证了 \(a_{i,j}\) 相邻数字的一致性,不过很难想到。
ZROI2840.千年红
结论:dfs 走出的树上全是返祖边,bfs 走出的树上全是横叉边。
当 \(n,m\) 比较小的时候,可以直接 dfs 构造出来一组全是返祖边的树,然后一条边一条边的调整。
但是可以更快,我们发现如果 \(u\) 有 \(k\) 个祖先边 \(e_1~e_2~e_3...e_k\) 本来是连着 \(e_1\),如果调整到 \(e_{t+1}\) 的话,就会少 \(t\) 条返祖边。于是我们可以正好凑出 \(a\) 条返祖边,然后 bfs。或者直接对于每个点记录所有祖先边,对 dfn 排序,然后从根最后遍历一遍调整。
记录下所有祖先边再最后上调这步是关键。
ZROI2928.无禅零区
非自同构图的构造。
考虑用若干颗小树拼接起来。特判 \(n=5,7\) 的基环树。
P11189 「KDOI-10」水杯降温
两种操作顺序不影响的题,可以考虑先进行某种操作再进行另一种。其中第一个进行的操作必须使得第二个进行的操作正好有可行性。
考虑先进行子树加操作,最后进行链减。可以发现为了使得链减合法,必须满足 \(a'_u=\sum\limits_{v\in son_u}a'_v\),且叶子节点权值 \(\ge 0\)。这样子就和链减无关了,只需要考虑通过子树加来构造出满足上述条件的树。
设 \(val_u\) 表示 \(u\) 以及其祖先执行子树加 \(1\) 操作的次数。\(val\) 肯定有约束的,第一感觉应该是一些很复杂的等式守恒。其实由于可以对于本身加,所以这其实是一个很松的限制,满足对于 \(v\in son(u)\),\(val_u\le val_v\)。
下面就是列式子了,\(a_u+val_u=\sum\limits_{v\in son(u)}a_v+val_v\)。
只需要我们找到一组符合要求的 \(\{val_n\}\) 即可。可以从叶子节点来从下往上推导。
其中对于叶子节点有最终 \(\ge 0\) 的约束,所以有 \(a_u+val_u\ge 0\)。然后依据这个来往上推祖先。由此可以看出每一个满足条件的 \(val_u\) 应该都是一个范围。
我们从下到上解 \([l_u,r_u]\) 代表 \(val_u\) 的范围。在 \(val_u\ge 0,val_v\ge val_u\) 的约束下考虑 \(v\to u\)。对于第一个条件我们可以在解出范围之后对于 \(0\) 取 \(\max\) 即可。对于第二个条件发现 \(val_u\) 越小越容易满足,所以我们贪心地调整所有 \(val_v\) 为 \(l_v\)。那么 \(l_u=-a_u+\sum\limits_{v\in son(u)}a_v+l_v\)。对于上界就有点难搞了,因为约束要求的是 \(val_u\) 尽可能小,而我们想最大化。这里有两种思路:一种是二分 \(val_u\) 的取值。第二种是发现 \(val_v\) 的防缩方向是 \(r_v\) 或者 \(val_u\),直接枚举取 \(val_u\) 的个数然后解不等式即可。
其实顺着我自己的思路走应该也是可以做出这题的,首先数学化这个过程。
那么每个点就是 \(a_u+\sum\limits_{v\in anc(u)} add_v-\sum\limits_{v\in leaf(u)} del_v=0\)。一个很暴力的想法就是 \(O(n^3)\) 来解这个方程,但是时间复杂度不对并不意味着我们不能从这里继续推到。
仔细分析一下,其实是可以发现方程的个数是要小于未知数的个数的,所以我们要求解的应该是未知数的一个范围而不是具体的值!而且这个 \(add\) 和 \(del\) 比较不太统一,尤其是 \(del\) 只有叶子节点处会产生,这启发我们定一个变量,动另外一个变量。我们固定 \(add\),考虑 \(del\)。
这是因为 \(del\) 的约束性和特殊性远远强于 \(add\)。列出 \(del\) 的约束方程,\(del_u=\sum\limits_{v\in son(u)} del_v\)。将上面列出的方程代入进行消元可以得到 \(a_u+sum_u=\sum\limits_{v\in anc(u)} a_v+add_v\)。
这样子一来不仅可以很自然的得到和第一种做法相同的方程式子(至少我是没想到可以先进行某一操作再利用另一个操作来进行调整),而且还可以启发我们得到解应该是一个范围。
CF1819E Roads in E City
本题中询问的联通性都是只是和特殊边相关的,和非特殊边没有啥关系,可以直接看成一张只有特殊边构成的图。于是问题就变成了有一张隐藏的图,给定一些可能在图上的边判断它们是否在图上。下文也是按照把特殊边和非特殊边改成是否在图上来写的。
首先还是交互题老套路,我们要思考如果构造一个良好的初始状态使得可以很好地通过询问来获得一些有效信息。
从全局角度直接对于整个图操作很难下手,我们不妨从每条边单独开始思考。
因为询问的是联通性,一次询问能产生贡献只有在图原本联通且断开一条边后某次询问得到了不可达的时候才能产生贡献,也就是可以帮助我们分辨这条边是不是在图上。
如果图原本不联通,那么不管是否断开这条边都有可能得到不可达的回复。所以要求一是初始状态的图必须满足可以通过没有被断的边联通。
如果我们断掉一条边的时候得到的回复是可达,那么说明这条边在不在图上都是一个效果,也就无法分辨它到底在不在图上了,这引导我们思考这条边如果是未断开边的桥的时候才能产生贡献。要求二是初始状态必须通过连/断边快速使得某条边成为未断边中的一个桥。
通过以上两个要求,我们可以发现原图的一个生成树是满足这个初始状态要求的。
因为首先树是联通的,其次对于一条边 \((u,v)\) 我们只需要断开树上 \(u-v\) 路径上的任意一条边再连上 \((u,v)\) 就可以使得 \((u,v)\) 变成桥了。
下面是本题的实现方法。
首先,需要找到一颗生成树。
一个图的生成树可以通过持续断开在残余图上的非桥边来得到。于是我们枚举每条边如果不是桥我们就删去,剩下的就是一颗生成树了。注意:不在原图上的边也会被上述过程删掉。于是剩下的边就是在原图上的边(特殊边)构成的生成树了。
上述一步构造了一个良好的初始状态。
接下来只需要再次枚举每一条边 \((u,v)\),然后断开 \(u-v\) 路径上的某条边再连上 \((u,v)\) 判定 \((u,v)\) 是不是桥即可。
最后一个问题是如何判定一条边是不是桥,假设目前断开了一个桥 \((u,v)\),那么图分成了两个分别包含 \(u\) 和 \(v\) 的联通块,因为交互库不会根据本次操作来确定另一点 \(s\),所以单次询问可以看成是随机的, 各询问 \(u,v\) 十次即可。
ABC239F Construct Highway
首先必须满足 \(\sum deg_i=2n-2\),在此基础上不能成环。
先讲述一下无边限制的做法。
思考一个顺序使得连出来的不成环,很容易想到按照“度数序”,即度数大的当度数小的父亲。一开始的想法是按照度数从小往大做,每个点通过成为 \(d_i-1\) 个点的父亲来消耗它的度数,最后剩一个度数来连其父亲。不过这是一个粗略的想法,实现不好就是错的,首先观察出任意时刻必然有度数为 \(1\) 的点,所以我们上述的做法根本不需要往下连边,只需要每次取度数为 \(1\) 的点往上连即可。
思考如果有若干给定边会怎么样,一个点显然不能和已有联通块内 \(\ge 2\) 个点连边,所以我们用并查集维护联通块,然后把一个联通块当成一个整体跑上述算法即可。
CF1844G Tree Weights
经典转化,看到树上距离不会处理就变成为深度。
其中 \(dep_1=0\),\(n-1\) 个方程,\(n-1\) 个未知数,暴力高斯消元可以在 \(O(n^3)\) 的时间内解出。观察到对于每一行矩阵有值的位置很少,应该是能在 \(O(n^2)\) 的时间内高斯消元的,但是这还不够。
发现这个 \(dep_{\operatorname{lca(u,v)}}\) 很烦人,其实如果题目满足了节点编号 \(fa_u<u\) 的话,我们甚至可以一位一位推出来所有的值,但是可能在求 \((i,i+1)\) 的时候,\(dep_{\operatorname{lca(u,v)}}\) 可能还没计算出来,因此我们希望隐藏其信息,有一个很巧妙的 Trick,就是直接在 \(\bmod 2\) 的意义下思考这个问题就可以很轻松地隐藏这个深度信息,这样子我们从头往后一个一个算就可以算出所有 \(dep_i\) 在 \(\bmod 2\) 意义下的值也就是二进制的第一位。如果我们继续在 \(\bmod 4\) 意义下考虑的话 \(2\times dep_{\operatorname{lca(u,v)}}\bmod 4\) 就等于 \(dep_{\operatorname{lca(u,v)}} \bmod 2\),这个信息我们在上一轮中已经得到了,所以可以直接用。
因此不断在 \(\bmod 2^k\) 位下思考就可以得到所有 \(dep\) 每一个二进制的信息,从而得到 \(dep\)。
时间复杂度 \(O(n\log V)\)。
最后注意题目要求,由于是要求正边权,因此需要检查是否 \(dep_u>dep_{fa_u}\)。
P11884 [RMI 2024] 拉面 / Ramen
第一次独立写出紫的交互题,开心。
首先这个问题肯定是不弱于给定你 \(a\) 序列然后求解最优排列的。于是先思考确定 \(a\) 序列之后的做法。
每个点都有一个唯一的选择面条种类,\(i\to p_i\)。
受到 P8095 [USACO22JAN] Cereal 2 S 的启发,对于任意一组对应关系 \(p\),我们是必定可以构造出一组解的。
于是直接去求这个最优数字就行了,然后在这个过程中可以得到每个人选择拉面种类,据此构造排列。
求解最优数字是一个很显然的网络流模型,可以用最小费用最大流。左部点为所有人记为 \(id1_i\),右部点为所有种类的面条记为 \(id2_j\)。
构图,\((s,id1_i,1,0)\),\((id2_i,t,1,0)\) 和 \((id1_i,id2_j,1,a_{i,j})\) 即可。其中前两个数字代表点的编号,后两个数字分别代表流量和边权。
流量限制保证了每个人都会选择一种不同的拉面,费用限制可以求出最小代价。
跑一遍网络流,根据每条边的流量情况可以得到每个人选择的拉面方案,\(i\to p_i\)。并且对于 \(i\),求出所有面条喜爱程度的排名 \(rk_{i,j}\),这个排序一下就行了。
如何构造方案呢?我用的是拓扑排序。
题目求的是吃面的顺序,我们考虑一个一个确定。能加入 \(i\) 当且仅当所有排名高于 \(p_i\) 的面都已经被之前的人所选择过了,那么 \(i\) 再选择的时候就必然能选到 \(p_i\)。
于是我们连边 \((j+n,i)\),其中 \(j\) 是 \(rk_{i,j}<rk_{i,p_i}\) 的所有点。并且连边 \((i,p_i)\)。这样子每次选完一个 \(i\) 之后就代表解锁了一种面条的约束,一个点的的所有约束被解除之后就可以选这个点了。这完美符合拓扑排序的过程。
这样子我们就做完了 \(a\) 存在情况的解答。
考虑如何对于隐藏的 \(a\) 数组求解?其实就是随机一些排列,对于得到的位置填一下即可。我是先把所有数字当第一个填一下,然后剩余的次数都随机。
我 assert 了一下,肯定是填不满的。但是其实如果随机了很多次都没出现的组合 \((i,j)\),说明排名序列的特性使得这些 \((i,j)\) 本来就难出现,很难出现的位置组合在最优解中显露出来的概率也很小因此是成立的,也确实能通过所有数据。其实我交了三次正解,第一次是 WA 了一个点,后两次都是 AC。
注意一下细节就是没有被填到的位置不能在网络流中连边。
P8494 [IOI 2022] 最罕见的昆虫
很有趣。先通过 \(n\) 次操作,不断加入昆虫,删除重复种类昆虫,求出总的种类数 \(c\)。
这个出现的最大次数条件其实很难用,注意到我们拥有删除操作,因此我们考虑固定一个阈值 \(B\),当加入某个昆虫之后,最大次数超过了 \(B\) 我们就删除,这样子我们能控制所有 \(>B\) 的出现次数都在 \(B\)。这样子我们就可以通过比较机器内的昆虫数以及 \(B\times c\) 的大小来检查是否所有数都 \(\ge B\)。
有了以上技术,我们就可以二分答案了,直接做是 \(O(n\log n)\) 的。
考虑加入以下若干优化,首先是一些常数优化二分上界设置为 \(\dfrac{n}{c}\)。二分之前随机打乱加入序列,如果中途出现已经 \(=c\times mid\) 的情况就直接合法退出二分过程。还有一些保证复杂度的优化,假设当前二分区间为 \([l,r]\),所有数肯定已经加入了 \(l\) 个在机器中,如果答案 \(\ge mid\),就保留目前机器中的所有昆虫不进行删除,后续不加入这些即可。如果答案 \(<mid\) 的话,每种昆虫只保留 \(mid\) 种,也就是说这轮中加入失败的昆虫后续也不进行加入。这样子能卡到 \(3n\)。
P8491 [IOI 2022] 囚徒挑战
构造策略状态自动机题。
每个人都不能往后传输一个太大状态的数,所以不能逐步传输 \(a\) 和 \(b\)。
考虑按位逐步做,如果当前位相同就传输下一位。
不一定是二进制,可以在每一次采取不同进制。可以直接 DP 出来,但是还是不能通过。可以发现由于 \(a\neq b\),所以如果遇到了一个最小数或者最大数可以直接得到结果,所以每一层可以压掉目前的最大数和最小数。
通过 dp 转移可以打表出来每次一次选择 \(f_i=\max j\times f_{i-j}+2\)。进行构造即可。
P12447 [COTS 2025] 砍树 / Stablo
经典构建一颗树的交互,这种题我们一般是要求出每个点的深度,然后按照深度分层加入。
本题中,我们先以 \(1\) 为根,然后剩下所有点按照深度排序。依次加入,这样子保证新加入的点一定是当前联通块的一个叶子节点。于是我们需要找到这个点 \(x\) 连向哪个点,可以使用边分治,找到一条边 \((u,v)\) 使得其两侧联通块大小尽量接近,然后 \((u,v,x)\) 即可得到 \(x\) 是在哪个联通块之中,递归下去即可。这是一个边分治的过程,由于这是一颗二叉树,所以边分治的复杂度是对的。
NFLS18046.最长路径
给定一张 DAG,其最长路是 \(d\),要求你删除不超过 \(\dfrac{\log_2d-\log_2l}{\log_2d}m\) 条边使得图的最长路不超过 \(l\)。
其实 DAG 的性质很少,无非就是 dp,或者按照距离/拓扑序给图分层。这里先按照 \(f_i\) 表示 \(i\) 点到最远终点的距离给图分层。
首先有一个类根号分治做法,按照 \(\dfrac{f_i}{l+1}\) 给图分组,我们只需要把组之间的边都删了就行了,这样子组内的最长路 \(\le l\)。也可以按照 \(f_i\bmod l+1\) 分组,这样子把组内边删了即可,组间最长路 \(\le l\)。你按照两个策略中选择一个更优的输出即可。但是这个做法显然没有那么精巧,也无法得到满分。
思考这个式子的含义,分子的意思是每次将图的最长路除以 \(2\),达到 \(l\) 量级所需要的操作次数。分母的意义就是把 \(d\) 分层 \(\log\) 组。考虑一些二进制相关,对于按照距离分层,对于距离/层建立线段树结构,\(f_i=x\),\(f_j=y\),\(x\oplus y\) 的最高位相等于他们在线段树上的 \(\rm LCA\)。如果把线段树的一层 \(d\) 给全部断掉,也就是断掉所有 \(\rm maxbit(x\oplus y)=d\) 的 \(x,y\) 层之间的连边,这个时候图上的最大长度会除以 \(2\),我们需要进行 \(\log d-\log l\) 次这种操作,而线段树具有 \(\log d\) 层,取最小的 \(\log d-\log l\) 删去即可。
P12784 [ICPC 2024 Yokohama R] Beyond the Former Explorer
首先有一个显然的二分做法,就是直接二分答案在哪一列。然后遍历列得到答案。可以通过两列之间左右箭头数量的大小关系得出终点在左还是在右。注意你不能对于一列的左右箭头进行二分,不然在数量相等的时候无法判断。必须对于两列之间的空隙二分,统计左边列的右箭头,右边列的左箭头,如果个数相等的话可以通过初始进入方向来判断。
可惜,这个做法常数过大,无法通过。
考虑对于行列同时二分,写成分治形式,行和列交替进行二分缩小。可以得到答案是处于一个矩形范围内,我们现在需要将这个矩形顺着红线一分为二。
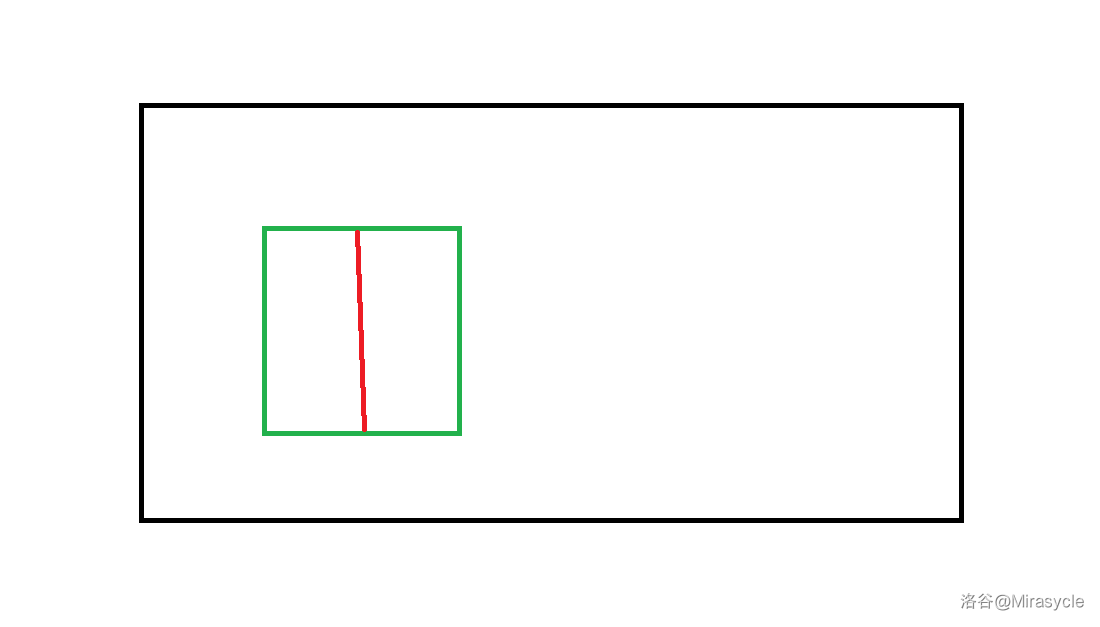
一个很直接的思路就是扫描这条红线,计算跨过其两边的次数。但是我们发现这条红线并没有抵住黑色方框的上下边界,所以我们统计到的跨越左右的次数是不完整的。
有一个巧妙的处理方法,将绿色方框内红线左边看成一个点,红线右边看成一个点,绿色框框之外黑框之内看成一个点。这样子我们有三个点,可以通过统计跨过红线的次数,跨过绿线的次数来得到三个点之间的有向边关系。于是整个问题就变成了欧拉路径问题!通过比较点 \((n+1,n+1)\) 和三个矩形的关系,我们可以得到起点是在哪个点内部。根据所有都要经过恰好一次边的信息,可以唯一确定终点。肯定不能直接模拟,我们考虑使用度数来解决这个问题,一个点能成为终点,要么其入读大于出度,要么其入度等于出度且其为起点。找到终点之后,直接往其中一个矩形递归即可。
每次对着红线两端行走一下即可,绿色的线两端不需要行走,因为绿线必定是之前某次的分割线,也就是意味着格子上面的值之前肯定走过了,我们用一个数组保存,调用之前的信息就行了。
最终的次数是 \(12n\) 左右。
P9074 [WC/CTS2023] 比赛
dmy 调整法的应用。
首先,需要判断无解。一般类似于相邻不能相同(本题是连续三个不能全部相同)这种问题的有解判定,都是只需要对于众数进行 check,因为一旦众数满足条件之后,其他的可以形如交替放或者两个两个放这种方法填满。于是本题有解的充要条件就是众数 \(\le \dfrac{2}{3}\) 总人数。
对于解的构造,引用邓老师在 UOJ 博客中的一句话。
调整法主要用于限制较松散的题目,要找到性质中松散/容易满足的那股劲。如果题目中有些限制难以满足,你就用人类智慧把它们先满足了,剩下的部分交给调整。不要让调整去摁做很严格的限制。
我们需要将最严的限制进行手动满足,其他的较为宽松的性质交给调整法。
最严的限制,自然就是众数,即人数最多的那个社团。我们优先将其满足,剩下的交给调整法。具体来说,我们先构造一个满足最严限制的初始情况,对于环上的连续位置按照每 \(3\) 个一组进行分组。一组之内放 \(\le 2\) 个该社团的人。然后将剩下的人随机填入。在调整的时候,我们每次随机两个交换的位置,如果交换完之后不合法三元组减少了就交换,如果不变就以 \(\dfrac{1}{2}\) 的概率接受。否则不接受。
注意几个细节: \(m\) 可能大于 \(2000\),可能有一些人不属于任何社团。
P12402 [COI 2025] 贪腐 / Korupcija
提供一种好写的神秘做法,就是按照 \(a_i\) 从小到大排序之后对于二进制位重标号,然后遍历 set 直接匹配。由 Purslane 在模拟赛中写出。尽管第一眼并不知道这个做法为什么对,但是如果拿一些失败的匹配策略和这个策略在样例上进行一些对比,再感受一下这个做法,你会感觉这个做法非常对。我思考了 2h 也无法严谨证明这个贪心。
考虑按位做这件事,比如我们从高位到低位来做,考虑一个线段树结构,一个二进制位代表一层的所有节点(每次匹配必须跨过这一层的恰好一个节点),叶子节点层不代表任何二进制位。每次匹配就是从左子树从选择一个点,匹配右子树的另一个点(左点固定后,这个右点唯一确定)。可以用 std::set 完成匹配。但是直接做自然是错的,因为你没办法通过匹配需求来合理分配。但是从这个做法中我们看出本题有解的条件,就是 \(a_i\) 必须是偶数,否则向下递归之后会出现某个子树内有奇数个点的情况,这自然无法匹配。
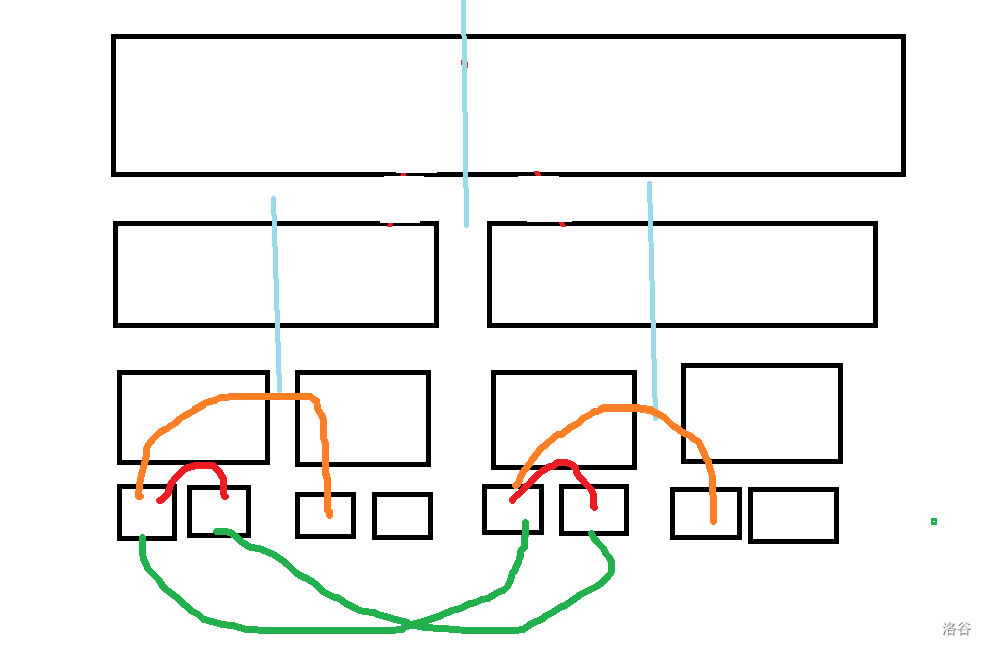
于是我们修改策略,按照 \(a_i\) 从大到小排序,按照这个顺序对于二进制位重标号之后进行匹配,这样子 \(a_i\) 比较大的二进制位会被优先满足,是不是更优呢?本题的第三个样例是一个很好的反例,我们会在第一层匹配的时候删掉第二层两个节点的左儿子所有点,导致进入第二层之后就无法匹配了
- 其实原本是否重标号对于二进制数是没什么影响的,但是我们遍历
std::set的时候,会按照数字从小到大的顺序遍历,所以就会有一些影响,为了按照一些我们需要的顺序匹配,就必须重标号。
上一个策略的失败,让我们意识到了其实上层对于下层的影响非常大,而且由于我们 set 的遍历方式(其实不管怎么遍历都会让某些层不均匀),这种做法会让一些东西被不均匀选择。于是我们转换思路,考虑按照 \(a_i\) 从小到大对于二进制位重标号,跑上述算法,会发现就对了!因为上层选的少代表对于下面的影响小,而且下层的节点个数更多,匹配选择更多样。
一层一层做,在某一层中我们按照从小到大枚举匹配(比如图中绿线),这样子必定会先把一些层中的某个节点的左子树给先选了一部分,比如在第一层中选绿线,会在第二层和第三层中分别各占用两个节点左子树内的所有点,我们称这种为"破坏匹配",因为只选左不选右会导致左右无法均衡匹配有点倒闭。而且我们会发现单次选择的破坏性很大,比如划过一条绿线之后,会导致两条橙线都无法匹配了!
\(1:2\) 的损耗无法接受,最多只能 \(1:1\),但是选了第二条绿线之后会发现这一次没有破坏红色匹配,因为之前已经破坏过了。所以填充了若干次之后会从下到上逐渐得恢复比例,上层个数少破坏掉一些也关系不大,但是无法严谨证明。
注意由于最高层是最高位,所以排序优先级高的二进制位(在排序后数组靠前位置的二进制位)反而应该被标更小的号。别写反了。
时间复杂度 \(O(n^22^n)\)。
P6541 [WC2018] 即时战略
点分树相关交互题。
先思考链怎么做,可以发现我们已经确定的位置一定是一个联通块,记为 \([l,r]\)。我们随机一个未确定的点 \(u\),可以通过一次询问得到 \(u\) 所在位置在 \(l\) 左边还是 \(r\) 右边,然后一路扩展过去即可。分析一下询问次数,扩展的时候一共会扩展 \(n-1\) 个节点,所以需要 \(n-1\) 次。关键是 \(u\) 每次询问方向的时候会多消耗一次。由于是随机的,所以每次长度会在某一侧期望缩减为原来的 \(\dfrac{1}{2}\)。询问期望次数是 \(O(\log n)\) 的。
对于树的情况,由于当前联通块会延伸出若干叶子节点(链的情况只有两个),所以我们不知道是在哪个叶子节点的子树内。于是考虑从根开始询问,不断跳儿子直到跳到某个叶子就可以进行扩展了。但是由于深度没有保证可能被卡到 \(O(n^2)\)。但是我们可以建立点分树结构来辅助跳跃的过程,由于点分树的树高是 \(O(\log n)\) 的,所以支持我们快速在树上进行暴力跳。
由于需要进行点扩展,所以是一个动态加点构建点分树的过程。我们可以定期重构点分树,由于点分树在一个分治中心下每个子树的大小应该是比较均匀的,所以我们在某个节点的子树大小大于它在点分树父亲节点的大小的 \(0.7\) 倍的时候重构其父亲点分树就行了。期望操作次数 \(O(n\log n)\)。
有一件很重要的事就是你在重构点分树的时候,不能访问点导出子图外的边,也就是不能遍历保存原图的 vector。
P9731 [CEOI2023] Balance
先考虑 \(S=2\) 的做法,我们使用欧拉回路解决。
对于 \(S\) 更大的做法,我们先做 \(S=2\) 然后分治下去。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号