斯特林数

斯特林数

斯特林数概述

在数学中，斯特林数 (Stirling) 用于解决各种数学分析和组合数学问题，斯特林数是两组不同的数，均是18世纪由 詹姆斯·斯特林 引入并以其命名，以第一类斯特林数和第二类斯特林数的称呼区分。此外，有时候也将拉赫数称为第三类斯特林数。

对于第一类斯特林数 \(s\left(n,m \right)\)，也可以记为 $ \left [ {\begin{matrix} n \ m \end{matrix}} \right ]$。表示将 n 个不同的元素构成 m 个圆排列的方案数。同时还分为无符号第一类斯特林数和有符号第一类斯特林数

第二类斯特林数 \(S(n, m)\) ，同时也可以记为 \(\left \{ {\begin{matrix} n\\ m \end{matrix}} \right \}\)。表示将 n 个不同的元素分为 m 个集合的方案数。

拉赫数与斯特林数关系密切，所以有时拉赫数也被称为 第三类斯特林数，将在文末探讨它的定义和一些简单性质。

第一类斯特林数

第一类斯特林数的定义

将 n 个元素，划分为 k 个圆排列的方案数，记作 \(s(n, m)\) 或者 \(\left[\begin{matrix} n \\ m\end{matrix} \right]\)。又根据正负性分为第一类斯特林数与第二类斯特林数。

圆排列：无头也无尾，两个圆排列相同当且仅当索取元素的个数相同并且元素取法一致，在环上的排列顺序一致。

递推求第一类斯特林数

我们考虑如何求解第一类斯特林数，一般首先考虑递推。

考虑这样一个问题：将 1 ~ n 的一个排列，划分为 k 个圆排列，一共有多少种方案？

分析第 n 个数 n，有哪些放置方法。发现有两种。一个是放在新的一个圆中，另一个是放到已有圆中。

所以此时的方案数等于：\(\left[\begin{matrix} n \\ k \end{matrix}\right]=\left[\begin{matrix} n-1 \\ k-1 \end{matrix}\right]+(n-1)\times \left[\begin{matrix} n-1 \\ k \end{matrix}\right] \\\)

递推边界：\(s(n, n) = 1, s(n, 0) = 0\)

第一类斯特林数表与斯特林三角

下表为无符号数斯特林数，如果想获得有符号斯特林数，可以通过它们之间的转换关系：\(s(n,k)=(-1)^{n-k}\left[\begin{matrix} n \\ k \end{matrix}\right]\)

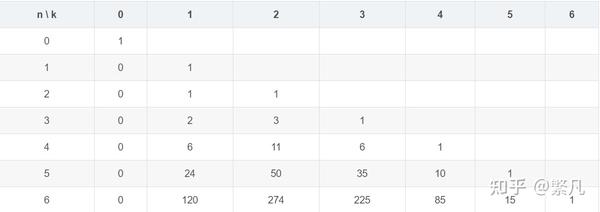
二项式系数 \(C\left(n,m\right)\) 可以构成一个杨辉三角（pascal三角形）。同样第一类斯特林数同样也可以构成一个三角如图13.1 所示，我们可以由此分析其性质。

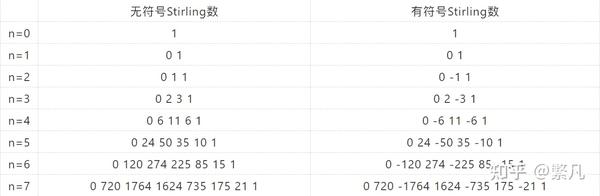
第一类斯特林数的性质

无符号第一类斯特林数的性质

• \(s_u\left(0,0\right)=1\)
• \(s_u\left(n,0\right)=0\)
• \(s_u\left(n,n\right)=1\)
• $ s_u\left(n,1\right)=\left(n-1\right)!$
• \(s_u\ (n,n-1)=\text C^{2}_{n}\)
• \(s_u\left(n,2\right)=\left(n-1\right)!\cdot\sum\limits_{i=1}^{n-1}\frac{1}{i}\)
• \(s_u\left(n,n-2\right)=2\cdot \text C^{3}_{n}+3\cdot \text C^{4}_{n}\)
• \(\sum\limits_{k=0}^ns_u\left(n,k\right)=n!\)

其中，最后一个式子的具体证明需要用到第一类斯特林数的生成函数——上升幂

对于 \(s_u(n, 2)\)，因为只有两个圆排列，我们可以考虑枚举每个圆排列的元素个数，假设第一个圆排列为 \(i\) 个，那么第二个圆排列元素就是 \(n - i\) 个。

所以此时方案数为：\(\dfrac{1}{2}C_n^{i}(i - 1)!(n - i - 1)!\)

我们考虑花间这个式子：

\[\dfrac{1}{2}C_n^{i}(i - 1)!(n - i - 1)! = \dfrac{1}{2} \times \dfrac{n!}{i!(n - i)!} \times (i - 1)!(n - i -1)! \\ = \dfrac{1}{2}\dfrac{n!}{i(n - i)} = \dfrac{1}{2} \times (n - 1)! (\dfrac{1}{i} + \dfrac{1}{n - i}) \]

所以方案总数是：

\[\sum\limits_{i = 1}^{n - 1} \dfrac{1}{2} (n - 1)!(\dfrac{1}{i} + \dfrac{1}{n - i}) = \dfrac{(n - 1)!}{2} \times 2 \times \sum\limits_{i = 1}^{n - 1} \dfrac{1}{i} = (n - 1)!\sum\limits_{i = 1}^{n - 1}\dfrac{1}{i} \]

上升幂与下降幂

我们记 上升阶乘幂 为 上升幂

\(x^{\overline{n}}=\prod\limits_{k=0}^{n-1} (x+k)=x(x+1)(x+2)\cdots(x+n-1) \\\)

普通的幂就是 $ x\times x\times x\times \cdots$，上升幂就可以形象地理解为 x 越乘越大，在往上升。

我们就可以利用下面的恒等式将上升幂转化为普通幂：

\(x^{\overline{n}}=\sum\limits_{k=0}^{n} \begin{bmatrix}n\\ k\end{bmatrix} x^k \\\)

如果将普通幂转化为上升幂则有下面的恒等式：

\(x^n = \sum\limits_{k} \begin{Bmatrix}n \\ k\end{Bmatrix} (-1)^{n - k}x^{\underline{k}}\)

我们记 下降阶乘幂（下降幂）

\(x^{\underline{n}}=\dfrac{x!}{(x-n)!}=\prod_{k=0}^{n-1} (x-k)\\\)

则可以利用下面的恒等式将普通幂转化为下降幂： \(x^n=\sum_{k} \begin{Bmatrix}n \\ k\end{Bmatrix} x^{\underline{k}}\\\)

如果将下降幂转化为普通幂，则有下面的恒等式：

\(x^{\underline{n}}=\sum_{k} \begin{bmatrix}n \\ k\end{bmatrix} (-1)^{n-k} x^k \\\)

多项式下降阶乘幂表示与多项式点值表示的关系

在这里，多项式的下降阶乘幂表示就是用 \(f(x)=\sum\limits_{i=0}^nb_i{x^{\underline{i}}} \\\)，的形式表示一个多项式，而点值表示就是用 n+1 个点

\((i,a_i),i=0\cdots n \\\) 来表示一个多项式。 显然，下降阶乘幂 b 和点值 a 间满足这样的关系：

\(a_k=\sum\limits_{i=0}^{n}b_ik^{\underline{i}} \\\)

即：

\(\begin{aligned} a_k&=\sum\limits_{i=0}^{n}\dfrac{b_ik!}{(k-i)!}\\\dfrac{a_k}{k!}&=\sum\limits_{i=0}^kb_i\dfrac{1}{(k-i)!} \end{aligned} \\\)

很明显这是一个卷积形式的式子，我们可以在 $\mathcal{O}(nlogn) $ 的时间复杂度内完成点值和下降阶乘幂的互相转化。

第二类斯特林数

第二类斯特林数的定义

第二类斯特林数实际上是集合的一个拆分，表示将 n 个不同的元素拆分成 m 个集合间有序（可以理解为集合上有编号且集合不能为空）的方案数，记为 \(S(n, m)\)，这里是大写的 S 或者 \(\begin{Bmatrix} n \\ m\end{Bmatrix}\)

和第一类斯特林数不同的是，这里的集合内部是不考虑次序的，而圆排列圆的内部是有序的。常常用于解决组合数学中的几类放球模型。描述为：将 n 个不同的求放入 m 个无差别的盒子里，要求盒子非空，有几种方案？

递推求第二类斯特林数

第二类斯特林数的推导和第一类斯特林数的推导类似

我们可以直接写出递推公式：

\[\begin{Bmatrix} n \\ k\end{Bmatrix} = \begin{Bmatrix} n - 1 \\ k - 1\end{Bmatrix} + k \times \begin{Bmatrix} n - 1 \\ k\end{Bmatrix} \]

边界条件：

\(S(n, n) = 1\)

\(S(n, 0) = 0\)

第二类斯特林数与斯特林三角

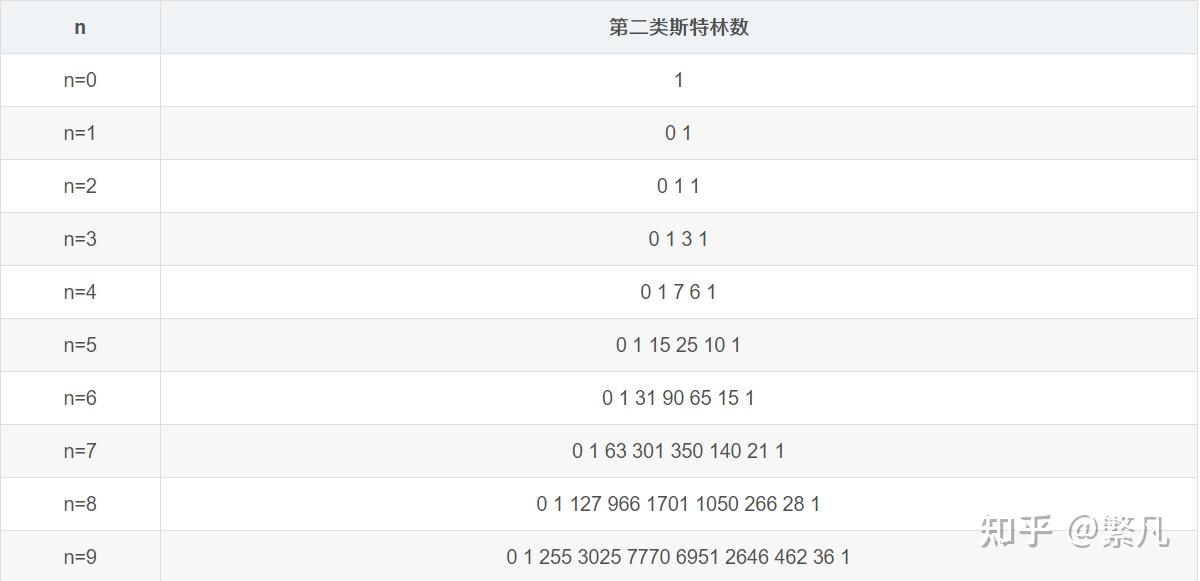
第二类斯特林数的性质

• \(S(n, 0) = 0\)
• \(S(n, 1) = 1\)
• \(S(n, n) = 1\)
• \(S(n, 2) = 2^{n - 1} - 1\)
• \(S(n, n - 1) = C_n^{2}\)
• \(S(n, n - 2) = C_n^{3} + 3 \times C_n^4\)
• \(S(n, 3) = \dfrac{1}{2}(3^{n - 1} + 1) - 2^{n - 1}\)
• \(\sum\limits_{k = 0}^{n}S(n, k) = B_n\)，其中 \(B_n\) 是贝尔数