双向搜索
双向搜索
介绍两种双向搜索算法,双向同时搜索 和 Meet in the middle
双向搜索
双向同时搜索的基本思路是从状态图上的起点和终点同时开始进行。
如果发现搜索的两端相遇了,那么可以认为是获得了可行解。
如果原本的答题树的规模是 \(a^{n}\) ,那么使用双向搜索后规模立刻缩小到了 \(2a^{n / 2}\) ,在 \(n\) 比较大的时候优化还是很可观的。
双向搜索主要有两种,双向 BFS 和 双向迭代加深
双向 BFS
与普通的 BFS 不同,双向 BFS 维护两个而不是一个队列,然后轮流扩展两个队列。同时,用数组(如果状态可以被表示为两个较小的整数)或哈希表记录当前的搜索情况,给从两个方向拓展的节点以不同的标记。当某个节点被两种标记同时标记时,搜索结束。
queue<T> Q[3]; // T要替换为用来表示状态的类型,可能为int,string还有bitset等
bool found = false;
Q[1].push(st); // st为起始状态
Q[2].push(ed); // ed为终止状态
for (int d = 0; d < D + 2; ++d) // D为最大深度,最后答案为d-1
{
int dir = (d & 1) + 1, sz = Q[dir].size(); // 记录一下当前的搜索方向,1为正向,2为反向
for (int i = 0; i < sz; ++i)
{
auto x = Q[dir].front();
Q[dir].pop();
if (H[x] + dir == 3) // H是数组或哈希表,若H[x]+dir==3说明两个方向都搜到过这个点
found = true;
H[x] = dir;
// 这里需要把当前状态能够转移到的新状态压入队列
}
if (found)
// ...
}
例题
[P1379 八数码难题](P1379 八数码难题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
对于这个题,我们可以使用一个九位数来存储当前的棋盘状态。
然后可以使用 map 来判重,判断当前状态是否已经被走到过。可以单向 BFS,也可以双向 BFS。但是本题已知答案的最终状态,所以双向 BFS 相对来说效率还是更高的。
双向 BFS 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int T = 123804765;
ll n;
int a[5][5];
int dx[5] = {-1, 1, 0, 0};
int dy[5] = {0, 0, -1, 1};
queue <ll> q;
map<ll, int> vis;
map<ll, ll> ans;
int main() {
scanf("%lld", &n);
if (n == T) {
printf("0\n");
return 0;
}
q.push(n); // 先初始化,将起点与终点两个状态都入队
q.push(T);
ans[n] = 0;
ans[T] = 1; // 注意终点初始化步数的时候要初始化为 1
vis[n] = 1;
vis[T] = 2;
while (!q.empty()) {
ll u = q.front();
q.pop();
ll cur = u;
int fx, fy, nx, ny;
for(int i = 3; i >= 1; --i) { // 将 long long 存储的数字转为棋盘
for (int j = 3; j >= 1; --j) {
a[i][j] = cur % 10, cur /= 10;
if (a[i][j] == 0) fx = i, fy = j;
}
}
for (int i = 0; i < 4; ++i) {
nx = fx + dx[i];
ny = fy + dy[i];
if (nx < 1 || nx > 3 || ny < 1 || ny > 3) continue;
swap(a[fx][fy], a[nx][ny]);
cur = 0; // 将改变后的棋盘转化为新的 long long 数字进行存储
for (int j = 1; j <= 3; ++j)
for (int k = 1; k <= 3; ++k)
cur = cur * 10 + a[j][k];
if (vis[cur] == vis[u]) { // 如果这个状态已经在同一起点开始遇到过,那么我们不可能答案更优,我们直接跳过
swap(a[fx][fy], a[nx][ny]);
continue;
}
if (vis[cur] + vis[u] == 3) { // 如果双向 BFS 已经相遇,表示我们已经找到了答案,直接输出。
printf("%d\n", ans[cur] + ans[u]);
system("pause");
return 0;
}
ans[cur] = ans[u] + 1;
vis[cur] = vis[u];
q.push(cur);
swap(a[fx][fy], a[nx][ny]); // 注意每一次处理完了以后都要恢复初始的状态,因为还要往别的方向去 BFS
}
}
system("pause");
return 0;
}
单向 BFS 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int T = 123804765;
int n, a[5][5];
int dx[5] = {-1, 1, 0, 0};
int dy[5] = {0, 0, -1, 1};
map<ll, int> ans;
int main() {
//freopen("data.in", "r", stdin);
//freopen("data.out", "w", stdout);
scanf("%lld", &n);
if (n == T) {
printf("0\n");
return 0;
}
queue <ll> q;
q.push(n);
ans[n] = 0;
while (!q.empty()) {
ll u = q.front();
q.pop();
ll cur = u;
int fx, fy, nx, ny;
for (int i = 3; i >= 1; --i) {
for (int j = 3; j >= 1; --j) {
a[i][j] = cur % 10, cur /= 10;
if (a[i][j] == 0) fx = i, fy = j;
}
}
for (int i = 0; i < 4; ++i) {
nx = fx + dx[i];
ny = fy + dy[i];
if (nx < 1 || nx > 3 || ny < 1 || ny > 3) continue;
swap(a[fx][fy], a[nx][ny]);
cur = 0;
for (int j = 1; j <= 3; ++j)
for (int k = 1; k <=3 ; ++k)
cur = cur * 10 + a[j][k];
if (ans[cur]) {
swap(a[fx][fy], a[nx][ny]);
continue;
}
ans[cur] = ans[u] + 1;
q.push(cur);
swap(a[fx][fy], a[nx][ny]);
if (cur == T) {
printf("%d\n", ans[cur]);
system("pause");
return 0;
}
}
}
system("pause");
return 0;
}
相比之下,此题单向 BFS 确实比双向 BFS 慢了不少。
[P2324 [SCOI2005]骑士精神]([P2324 SCOI2005]骑士精神 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
我们发现这个题目与上一个差不多。对于末状态我们已经确定,初状态也有,所以我们可以采取双向搜索。而且题目要求在 15 步以内,也就是说遇到步数大于15 的时候我们直接停止该点的继续搜索即可。
#include <bits/stdc++.h>
using namespace std;
int t, x, y;
char a[10][10];
int dx[] = {-1, 1, -1, 1, -2, 2, 2, -2};
int dy[] = {-2, 2, 2, -2, -1, 1, -1, 1};
inline int read() {
int x = 0, f = 1;
char c = getchar();
while (!isdigit(c)) {
if (c == '-') f = -1;
c = getchar();
}
while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
return x * f;
}
inline void get_position(string str) {
int len = str.length();
for (int i = 0; i < len; ++i)
if (str[i] == '*') x = i / 5 + 1, y = i - (x - 1) * 5 + 1;
int l, r;
for (int i = 0; i < len; ++i) {
l = i / 5 + 1;
r = i - (l - 1) * 5 + 1;
a[l][r] = str[i];
}
}
int main() {
//std::ios::sync_with_stdio(false);
t = read();
while (t--) {
unordered_map<string, int> ans;
unordered_map<string, int> vis;
string start, en;
for (int i = 1; i <= 5; ++i) {
for (int j = 1; j <= 5; ++j) {
cin >> a[i][j];
start = start + a[i][j];
}
}
queue <string> q;
en = "111110111100*110000100000";
vis[start] = 1;
vis[en] = 2;
ans[start] = 0;
ans[en] = 1;
q.push(start), q.push(en);
int fx, fy, nx, ny;
int flg = 0;
while (!q.empty()) {
string u = q.front();
q.pop();
get_position(u);
fx = x, fy = y;
for (int i = 0; i < 8; ++i) {
string cur = "";
nx = fx + dx[i], ny = fy + dy[i];
if (nx < 1 || nx > 5 || ny < 1 || ny > 5) continue;
swap(a[fx][fy], a[nx][ny]);
for (int i = 1; i <= 5; ++i)
for (int j = 1; j <= 5; ++j)
cur = cur + a[i][j];
if (vis[cur] == vis[u]) {
swap(a[fx][fy], a[nx][ny]);
continue;
}
if (vis[cur] + vis[u] == 3) {
printf("%d\n", ans[cur] + ans[u]);
flg = 1;
break;
}
ans[cur] = ans[u] + 1;
vis[cur] = vis[u];
q.push(cur);
swap(a[fx][fy], a[nx][ny]);
if (ans[cur] + ans[u] > 15) {
printf("-1\n");
flg = 1;
break;
}
}
if (flg) break;
}
}
return 0;
}
我们仍然使用 map 来判断是否重复情况。其实感觉也可以对于当前棋盘状态进行哈希,存储下来。
[P1032 [NOIP2002 提高组] 字串变换]([P1032 NOIP2002 提高组] 字串变换 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
一道初始状态与末状态都给到我们的题目。又是求解最优解,所以我们可以采用双向 BFS 方法。
考虑如何存储当前字符串的状态,可以 map 也可以进行哈希。方便起见,我们直接 map 就可以。
#include <bits/stdc++.h>
using namespace std;
const int N = 200000;
map<string, int> vis;
map<string, int> ans;
string s1, s2;
queue <string> q;
string from[N], to[N];
int main() {
//freopen("test.in", "r", stdin);
//freopen("data.out", "w", stdout);
cin >> s1 >> s2;
int id = 0;
string x, y;
while (cin >> x >> y) {
from[++id] = x;
to[id] = y;
}
vis[s1] = 1;
vis[s2] = 2;
ans[s1] = 0;
ans[s2] = 1;
q.push(s1), q.push(s2);
while (!q.empty()) {
string u = q.front();
q.pop();
int len = u.length();
for (int i = 0; i < len; ++i) {
if (vis[u] == 1) {
for (int j = 1; j <= id; ++j) {
int flg = 1;
for (int k = 0; k < from[j].length(); ++k) {
if (from[j][k] != u[i + k]) {
flg = 0;
break;
}
}
if (!flg) continue;
string cur = u.substr(0, i) + to[j] + u.substr(i + from[j].length(), len);
if (vis[cur] == vis[u]) continue;
if (vis[cur] + vis[u] == 3) {
printf("%d\n", ans[u] + ans[cur]);
system("pause");
return 0;
}
if (ans[cur] + ans[u] > 10) {
printf("NO ANSWER!\n");
return 0;
}
vis[cur] = vis[u];
ans[cur] = ans[u] + 1;
q.push(cur);
}
} else if (vis[u] == 2) {
for (int j = 1; j <= id; ++j) {
int flg = 1;
for (int k = 0; k < to[j].length(); ++k) {
if (to[j][k] != u[i + k]) {
flg = 0;
break;
}
}
if (!flg) continue;
string cur = u.substr(0, i) + from[j] + u.substr(i + to[j].length(), len);
if (vis[cur] == vis[u]) continue;
if (vis[cur] + vis[u] == 3) {
printf("%d\n", ans[u] + ans[cur]);
system("pause");
return 0;
}
if (ans[cur] + ans[u] > 10) {
printf("NO ANSWER!\n");
return 0;
}
vis[cur] = vis[u];
ans[cur] = ans[u] + 1;
q.push(cur);
}
}
}
}
printf("NO ANSWER!\n");
return 0;
}
但是这一道题目有点特殊的是,从初始状态开始 BFS 的点与从末尾状态开始 BFS 的点要分开处理,因为一个是变过去,一个是变回来。
然后感觉自己对于 string 的一些函数还不是很熟悉,还是慎用吧。
[编辑书稿 Editing a Book](编辑书稿 Editing a Book - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, a[15], b[15], id;
map<int, int> vis;
map<int, int> ans;
inline int read()
{
int x = 0, f = 1;
char c = getchar();
while (!isdigit(c))
{
if (c == '-')
f = -1;
c = getchar();
}
while (isdigit(c))
x = x * 10 + c - '0', c = getchar();
return x * f;
}
int main()
{
while (true)
{
++id;
n = read();
if (!n)
return 0;
int status = 0, x;
for (int i = 1; i <= n; ++i)
{
x = read();
status = status * 10 + x;
}
int en = 0;
for (int i = 1; i <= n; ++i)
en = en * 10 + i;
if (en == status)
{
printf("Case %d: 0\n", id);
continue;
}
vis.clear();
ans.clear();
vis[status] = 1;
vis[en] = 2;
ans[status] = 0;
ans[en] = 1;
queue<int> q;
q.push(status), q.push(en);
// cout << "status: " << status << endl << "en: " << en;
while (!q.empty())
{
int cur_status = q.front(), cur;
q.pop();
cur = cur_status;
for (int i = 1; i <= n; ++i)
{
a[i] = cur % 10;
cur /= 10;
}
std::reverse(a + 1, a + 1 + n);
int flg = 0;
for (int i = 1; i <= n; ++i)
{ // 寻找截取哪一段
for (int j = i; j <= n; ++j)
{
for (int p = 1; p <= n + 1 && !(p > i && p <= j); ++p)
{
int len = 0;
flg = 0;
memset(b, 0, sizeof(b)); // 寻找插入的位置
for (int k = 1; k <= p - 1; ++k)
{
if (k >= i && k <= j)
continue;
b[++len] = a[k];
} // 先继承
for (int k = i; k <= j; ++k)
b[++len] = a[k];
for (int k = p; k <= n; ++k)
{
if (k >= i && k <= j)
continue;
b[++len] = a[k];
}
int change_status = 0;
for (int i = 1; i <= len; ++i)
change_status = change_status * 10 + b[i];
// cout << "cur_status" << cur_status << endl << "change_status: " << change_status << endl;
if (vis[change_status] == vis[cur_status])
continue;
if (vis[change_status] + vis[cur_status] == 3)
{
printf("Case %d: %d\n", id, ans[change_status] + ans[cur_status]);
flg = 1;
break;
}
vis[change_status] = vis[cur_status];
ans[change_status] = ans[cur_status] + 1;
q.push(change_status);
}
if (flg)
break;
}
if (flg)
break;
}
if (flg)
break;
}
}
}
双向迭代加深
首先简单介绍一下单向迭代加深。
迭代加深算法就是控制 dfs 的最大深度,如果深度超过最大深度就返回。某个深度搜索完后没有得到答案便将最大深度 +1,然后重新开始搜索。
虽然看起来这个方法重复搜索了很多次而且和广搜差不多,但是搜索的时间复杂度几乎完全由解答树的最后一层确定,所以它与 BFS 在时间上只有常数级别的差距。换来的优势是:空间占用很小,有时候方便剪纸、方便传参等。
双向迭代加深就是相应地,从两个方向迭代加深搜索。先从起点开始搜 0 层,再从终点开始搜 0 层,然后循环迭代。
int D;
bool found;
template <class T>
void dfs(T x, int d, int dir) {
if (H[x] + dir == 3)
found = true;
H[x] = dir;
if (d == D)
return;
// 这里需要递归搜索当前状态能够转移到的新状态
}
// 在main函数中...
while (D <= MAXD / 2) { // MAXD为题中要求的最大深度
dfs(st, 0, 1); // st为起始状态
if (found)
// ...
// 题中所给最大深度为奇数时这里要判断一下
dfs(ed, 0, 2); // ed为终止状态
if (found)
// ...
D++;
}
例题
[P1379 八数码难题](P1379 八数码难题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
我们仍然是以这个题为例题,但是双向迭代深搜的效率要比双向 BFS 低很多,有一个点会 T 掉。
#include <bits/stdc++.h>
using namespace std;
int e[] = {1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000}, D;
bool found;
unordered_map<int, int> H;
inline int at(int x, int i) { return x % e[i + 1] / e[i]; }
inline int swap_at(int x, int p, int i) { return x - at(x, i) * e[i] + at(x, i) * e[p]; }
void dfs(int x, int p, int d, int dir) { // d 表示当前搜索到了第几层 dir 表示是从起点还是终点开始搜索
if (H[x] + dir == 3)
found = true;
H[x] = dir;
if (d == D)
return;
// p表示0的位置,这是比BFS好的一点,用BFS的话要专门开结构体储存p,或者现算
if (p / 3)
dfs(swap_at(x, p, p - 3), p - 3, d + 1, dir);
if (p / 3 != 2)
dfs(swap_at(x, p, p + 3), p + 3, d + 1, dir);
if (p % 3)
dfs(swap_at(x, p, p - 1), p - 1, d + 1, dir);
if (p % 3 != 2)
dfs(swap_at(x, p, p + 1), p + 1, d + 1, dir);
}
int main() {
int st, p, ed = 123804765;
cin >> st;
for (p = 0; at(st, p); ++p); // 找到起始状态中0的位置
while (1) {
dfs(st, p, 0, 1);
if (found) {
cout << D * 2 - 1;
break;
}
dfs(ed, 4, 0, 2);
if (found) {
cout << D * 2;
break;
}
D++;
}
return 0;
}
Meet in the middle
引入
Meet in the middle 算法没有正式译名,常见的翻译为 「折半搜索」、「双向搜索」或「中途相遇」。
它适用于输入数据较小,但还没有小到可以暴力搜索。
过程
Meet in the middle 算法的主要思想是将整个搜索过程分为两半,分别搜索,最后将两半的结果合并。
性质
暴力搜索的复杂度往往是指数级的,而改用 Meet in the middle 算法后的复杂度的指数可以减半,即让复杂度从 \(O(a^{b})\) 降到 \(O(a^{b / 2})\)
例题
[P4799 [CEOI2015 Day2] 世界冰球锦标赛]([P4799 CEOI2015 Day2] 世界冰球锦标赛 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
在 M 比较小的时候,我们发现就是一个背包。但是此题 M 很大,所以排除 dp 的想法。
我们尝试搜索,但是裸的搜索时间复杂度为 \(O(2^{40})\) 显然会 T,利用 meet in the middle 思想,将前一半搜索的状态存入 a 数组,后一半状态存入 b 数组。
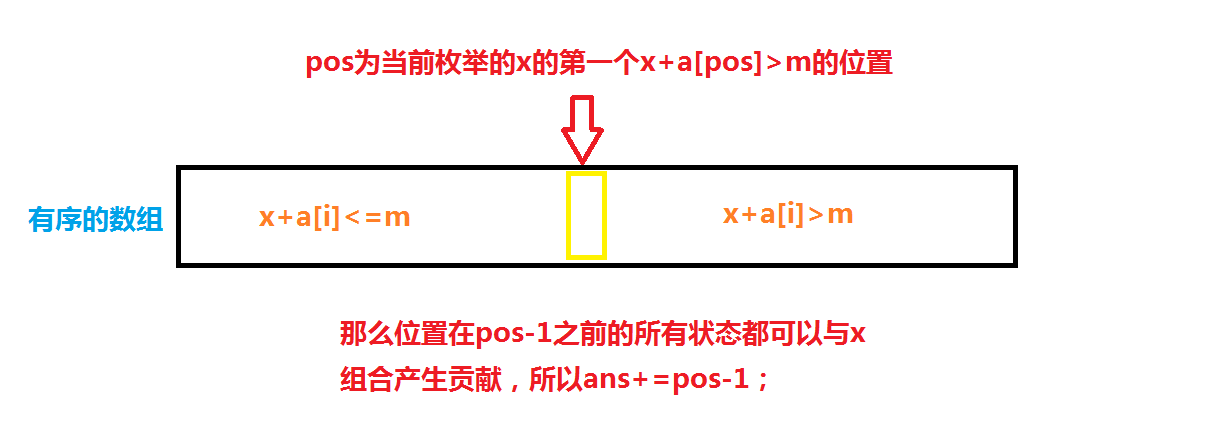
一般 meet in the middle 的难点主要在于最后答案的统计。我们可以将 a 或者 b 数组 sort,让其有序。然后通过枚举另一个数组中的状态,来实现统计答案。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 50;
ll n, cnt1, cnt2;
ll c[1 << 21], d[1 << 21];
ll m, a[N];
inline ll read() {
ll x = 0, f = 1;
char c = getchar();
while (!isdigit(c)) {
if (c == '-') f = -1;
c = getchar();
}
while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
return x * f;
}
inline void dfs(ll l, ll r, ll &cnt, ll ans[], ll remaining) {
if (l > r) {
ans[++cnt] = remaining;
return ;
}
dfs(l + 1, r, cnt, ans, remaining);
if (remaining - a[l] >= 0) dfs(l + 1, r, cnt, ans, remaining - a[l]);
}
int main() {
n = read(), m = read();
for (int i = 1; i <= n; ++i) a[i] = read();
ll mid = n >> 1;
dfs(1, mid, cnt1, c, m);
dfs(mid + 1, n, cnt2, d, m);
sort(c + 1, c + cnt1 + 1);
ll ans = 0;
for (int i = 1; i <= cnt2; ++i)
ans += cnt1 - (lower_bound(c + 1, c + 1 + cnt1, m - d[i]) - c - 1);
printf("%lld\n", ans);
system("pause");
return 0;
}
[P2962 [USACO09NOV]Lights G]([P2962 USACO09NOV]Lights G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))


 浙公网安备 33010602011771号
浙公网安备 33010602011771号