结对项目作业

项目	内容
所属课程	2020年春季计算机学院软件工程(罗杰任健)
作业要求	结对项目作业
课程目标	切身参与完整的软件开发流程，积累专业技术知识和团队合作经验
本次作业实现方面	参与体验完整的两人结对开发流程，并了解更为真实的软件开发(需求变更、错误处理、UI界面)
教学班级	006(周五上午三四节)
项目地址	https://github.com/Pupil59/PairWork

一、PSP表格

PSP2.1	Personal Software Process Stages	预估耗时(分钟)	实际耗时(分钟)
Planning	计划
· Estimate	· 估计这个任务需要多少时间	20	30
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	200	180
· Design Spec	· 生成设计文档	20	30
· Design Review	· 设计复审 (和同事审核设计文档)	20	10
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	10	10
· Design	· 具体设计	150	120
· Coding	· 具体编码	1000	900
· Code Review	· 代码复审	60	60
· Test	· 测试（自我测试，修改代码，提交修改）	200	300
Reporting	报告
· Test Report	· 测试报告	20	30
· Size Measurement	· 计算工作量	20	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	20
	合计	1550	1600

二、接口的设计

我们这一次的接口设计是以信息隐藏为主要方法的，且并不是简单的自定义类的成员属性的隐藏，而是将所有自定义类和成员方法以及存储结构都进行了封装，外界使用DLL时无需再导入几何对象自定义类的声明头文件以及对应的实现文件，即调用DLL的用户无需关心有哪些自定义几何对象类存在以及他们的实现方法，只能通过DLL模块的预留接口addLine()、addCircle()、delLine()、delCircle()并传入基本类型(string、int等)的参数来进行交互，并通过showLine()、showCircle()来展示DLL内部存储结构内的对象，从而实现了良好的封装和信息隐藏。

松耦合原则我们则是运用到了各个接口函数的功能设计上，保证了独立和互不影响，对于需求的变动会有很强的适应性，需求改变后需要编写和调整的范围会十分有限。

三、计算模块的设计与实现

由于新增的两类几何对象(射线和线段)与原有的几何对象(直线)只有起点终点的区别，故决定沿用我在上一次项目中的算法，保持lineIntersectLine()、lineIntersectCircle()、circleIntersectCircle()三个函数基本不变。先将所有线都视为直线调用之前的算法得到交点，在将交点加入结果集合之前多一次判断，判断该点是否在射线或线段的范围之内，来确定是否真正是我们想要的交点，从而得到正确的最终结果。这样的做法可以最大程度的利用之前的项目，只需添加判断函数即可。

将线段和射线设计成原有直线类Line的两个子类SegmentLine和RaysLine，继承原有的直线一般式的a，b，c三个参数，并添加新的属性记录起始点和方向等。存储结构也利用这一继承关系，直接将所有读入的线都向上转化为Line类，并将指针存入lines中，在需要区分类型时，使用虚函数isInLine()实现了每个类各自不同的判断方法，在调用时只需l.isInLine()而无需手动区分l的类型，十分简便。

vector<Line*> lines;
class Line {
public://使用一般式表示直线，避免使用double出现精度损失，在构造时求公因数化为最简。
	long long a;
	long long b;
	long long c;
	virtual bool isInLine(double x, double y) {
            Line l(x1, y1, x2, y2);
	    if (a == l.a && b == l.b && c == l.c) {
	    	return true;
	    }
	    return false;
        }
};
class SegmentLine : public Line {
public:
	long long startX;
	long long startY;
	long long endX;
	long long endY;
	bool isInLine(double x, double y) {
            if (startX == endX) {
		if ((y < startY && (startY - y) > 1e-8) || (y > endY && (y - endY) > 1e-8)) {
			return false;
		}
	    }
	    else {
		if ((x < startX && (startX - x) > 1e-8) || (x > endX && (x - endX) > 1e-8)) {
			return false;
		}
	    }
            return true;
        }
};

class RaysLine : public Line {
public:
	long long startX;
	long long startY;
	int direct;//1代表x轴正方向，2代表x轴负方向，3代表y轴正方向， 4代表y轴负方向
	bool isInLine(double x, double y) {
            switch (this->direct)
	    {
	        case 1:
		    if (x < startX && (startX - x) > 1e-8) {
			return false;
		    }
		    break;
	        case 2:
		    if (x > startX && (x - startX) > 1e-8) {
			return false;
		    }
		    break;
	        case 3:
		    if (y < startY && (startY - y) > 1e-8) {
			return false;
		    }
		    break;
	        case 4:
		    if (y > startY && (y - startY) > 1e-8) {
			return false;
		    }
		    break;
	    }
	    return true;
        }
};

将上一次项目中的几何对象两两相交的三个循环封装为最终的对外接口solve()：

int solve() {
	points.clear();
	for (int i = 0; i < (int)lines.size(); ++i) {//直线与直线相交
		for (int j = i + 1; j < (int)lines.size(); ++j) {
			lineIntersectLine(*lines[i], *lines[j]);
		}
	}
	for (int i = 0; i < (int)lines.size(); ++i) {//直线与圆相交
		for (int j = 0; j < (int)circles.size(); ++j) {
			lineIntersectCircle(*lines[i], circles[j]);
		}
	}
	for (int i = 0; i < (int)circles.size(); ++i) {//圆与圆相交
		for (int j = i + 1; j < (int)circles.size(); ++j) {
			circleIntersectCircle(circles[i], circles[j]);
		}
	}
	return (int)points.size();
}

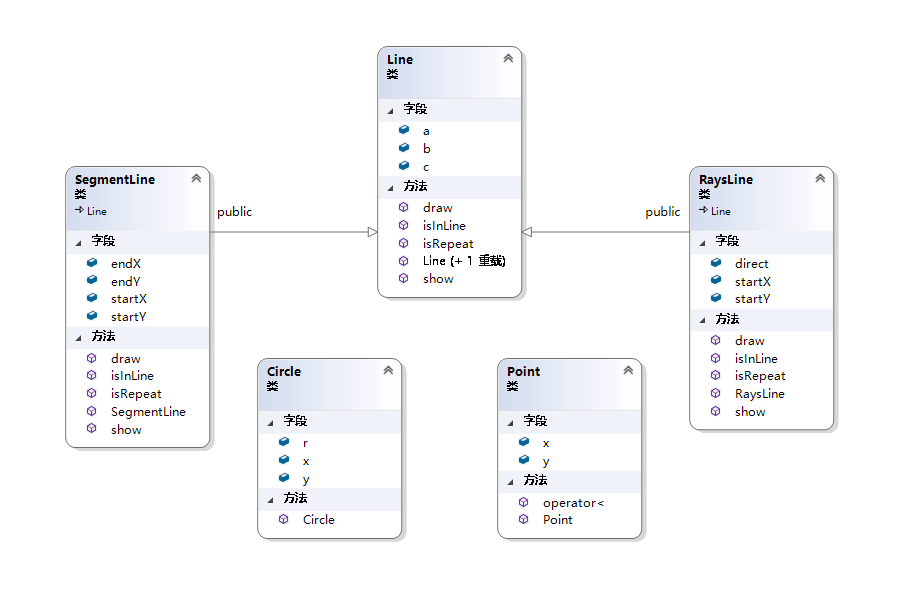
四、UML类图

由于两两相交的函数没有写成自定义的几何对象类的成员方法，故各个类之间的关系比较简单，只有射线和线段对于Line类的继承关系以及一些用于实现多态的虚函数。

五、性能分析图

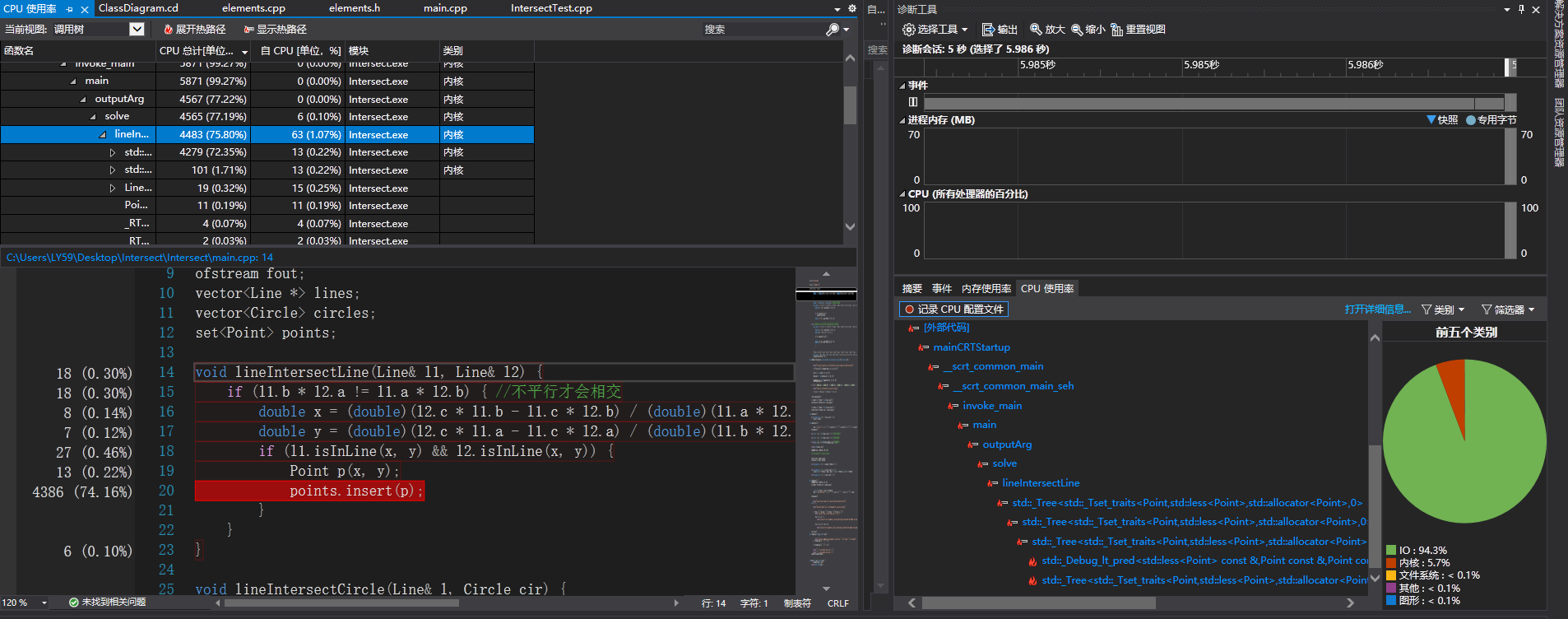
程序中消耗最大的函数是向保存结果的points集合中插入新点时的插入函数points.insert()，由于沿用了上一次项目中的整体结构，故这一性能问题依然存在，在上一次的项目中我曾提到使用unsorted_set可以减少插入时的比较次数，但由于本次项目增加了UI展示，我们的设计想法是支持在图上绘制交点的同时将交点的具体坐标信息也同时列出来，故就需要按照一定的顺序以便用户进行对应，这里set的排序功能正好发挥用处，故就没有使用unsorted_set。

六、契约式编程

契约式编程规定软件设计者应该为软件组件定义正式的，精确的和可验证的接口规范，该规范扩展了抽象数据类型的普通定义，包括前置条件，后置条件和不变量。
优点：

为开发者提供明确的设计目标和方向。
方便测试者进行测试。
为使用者提供明确的用途，让使用者在不了解具体细节的前提下就可以预期其行为。

缺点：

需要学习和掌握有关方面的标准和知识，学习成本高。
对于复杂的功能较难给出简洁易懂的约定。
撰写契约本身需要耗费一定的时间，且考虑情况不完备的契约对于之后的开发和测试有着严重影响。

在本次的项目中，我们没有按照标准的契约式编程流程进行，即没有对于函数的前置后置条件以及不变量进行书面的定义和约定，这实际上也和我们结对编程的方式有关，按照教材中所提的驾驶员和领航员角色，我们两人在编程过程中总是一起行动的，故可以实时的交流想法，不需要把对于某个接口的设计想法转成契约的形式传达给对方，直接交流更可以保证效率。对于大型的团队项目，每个人有明确的身份，设计与开发相分离的情况，契约式编程可能更为适用。

七、计算模块单元测试

由于算法沿用上一次的项目，整体结构都没有太大变化，增加了两个新的类SegmentLine和RaysLine以及判断是否在范围内的成员方法isInLine()，故对新增部分进行重点测试。(TestMethod1~11沿用了上一次测试的内容，对于直线和圆的各类关系都进行了覆盖)

                TEST_METHOD(TestMethod12)
		{//射线与直线不相交（即交点不在射线范围内，分四个位置测试），相交的情况就与直线与直线相交是一致的，不必重复测。
			Line l1(0, 1, 1, 0);
			RaysLine r1(1, 1, 2, 2);
			lineIntersectLine(l1, r1);
			Assert::AreEqual((int)points.size(), 0);
			RaysLine r2(1, 1, 1, 2);
			lineIntersectLine(l1, r2);
			Assert::AreEqual((int)points.size(), 0);
			RaysLine r3(0, 0, -1, -1);
			lineIntersectLine(l1, r3);
			Assert::AreEqual((int)points.size(), 0);
			RaysLine r4(-1, -1, -1, -2);
			lineIntersectLine(l1, r4);
			Assert::AreEqual((int)points.size(), 0);
			points.clear();
		}
		TEST_METHOD(TestMethod13)
		{//线段与直线不相交（即交点不在线段范围内，分四个位置测试），相交的情况同上，不必重复测。
			Line l1(0, 1, 1, 0);
			SegmentLine s1(1, 1, 2, 2);
			lineIntersectLine(l1, s1);
			Assert::AreEqual((int)points.size(), 0);
			SegmentLine s2(1, 1, 1, 2);
			lineIntersectLine(l1, s2);
			Assert::AreEqual((int)points.size(), 0);
			SegmentLine s3(1, 2, 1, 1);
			lineIntersectLine(l1, s3);
			Assert::AreEqual((int)points.size(), 0);
			SegmentLine s4(-1, -1, -2, -2);
			lineIntersectLine(l1, s4);
			Assert::AreEqual((int)points.size(), 0);
			SegmentLine s5(-1, -1, -1, -2);
			lineIntersectLine(l1, s5);
			Assert::AreEqual((int)points.size(), 0);
			points.clear();
		}
		TEST_METHOD(TestMethod14)
		{//射线与圆相交
			Circle c1(0, 0, 1);
			RaysLine r1(0, 1, 1, 1);
			lineIntersectCircle(r1, c1);
			Assert::AreEqual((int)points.size(), 1);
			Assert::AreEqual(points.begin()->x, 0.0);
			Assert::AreEqual(points.begin()->y, 1.0);
			points.clear();
		}
		TEST_METHOD(TestMethod15)
		{//线段与圆相交
			Circle c1(0, 0, 1);
			SegmentLine s1(0, 1, 0, -1);
			lineIntersectCircle(s1, c1);
			Assert::AreEqual((int)points.size(), 2);
			set<Point>::iterator it = points.begin();
			Assert::AreEqual(it->x, 0.0);
			Assert::AreEqual(it->y, -1.0);
			it++;
			Assert::AreEqual(it->x, 0.0);
			Assert::AreEqual(it->y, 1.0);
			points.clear();
		}

		TEST_METHOD(TestMethod16)
		{//solve函数测试
			Line* l = new Line(-1, 4, 4, -1);
			SegmentLine* s = new SegmentLine(0, 0, 1, 2);
			Circle c1(1, 0, 2);
			Circle c2(2, 2, 1);
			Circle c3(3, -2, 6);
			lines.push_back(l);
			lines.push_back(s);
			circles.push_back(c1);
			circles.push_back(c2);
			circles.push_back(c3);
			solve();
			Assert::AreEqual((int)points.size(), 6);
			lines.clear();
			circles.clear();
			points.clear();
		}

代码覆盖率：

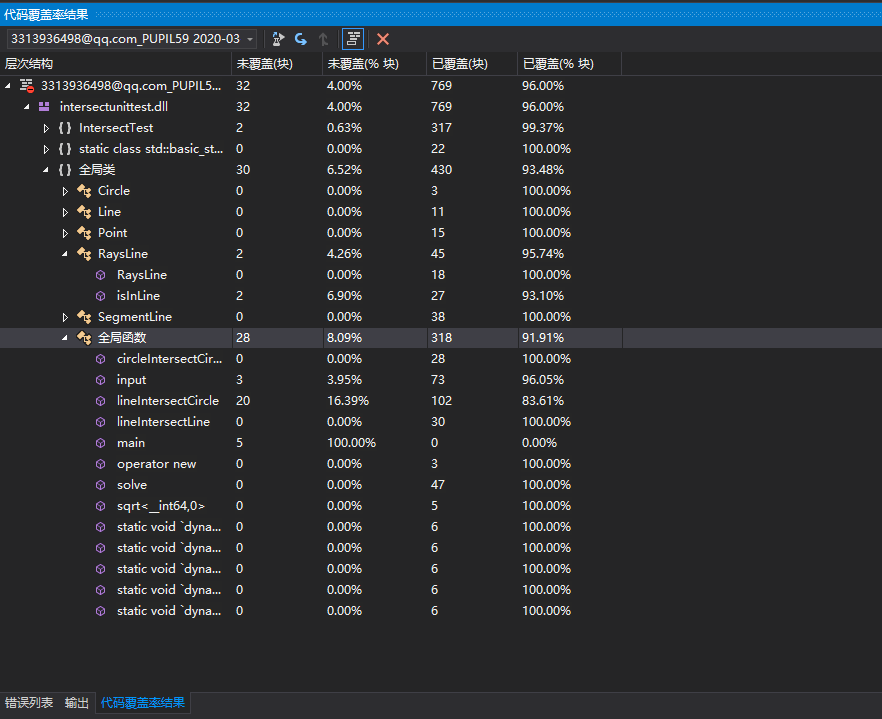
八、异常处理

由于最终的目标是要向用户显示错误提示，故我们没有特别设计异常类，只是采用了throw异常信息字符串的方法表示异常，在外层使用try-catch进行捕获。

命令行类错误：错误的命令行参数、未使用-i指明输入文件、未使用-o指明输入文件

　　　　　　　　　TEST_METHOD(TestMethod21)
		{
			try {
				char* argv[5] = { "Intersect.exe", "-v", "in.txt", "-o", "out.txt" };
				inputArg(5, argv);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "Incorrect command line parameters, please use '-i' for input, '-o' for output");
			}
			try {
				char* argv[5] = { "Intersect.exe", "iii", "in.txt", "-o", "out.txt" };
				inputArg(5, argv);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "'-i' is not found, please use '-i'");
			}
			try {
				char* argv[5] = { "Intersect.exe", "-i", "in.txt", "oooo", "out.txt" };
				inputArg(5, argv);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "'-o' is not found, please use '-o'");
			}
			fin.close();
		}

文件输入错误：未找到文件、几何对象数目错误(缺失、不为数字)、几何对象类型错误(不为所要求的字符)、几何对象参数错误(缺失、不为数字)

　　　　　　　　　TEST_METHOD(TestMethod22)
		{
			try {
				char* path = "int.txt";
				inputFile(path);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "can not locate input file, please check the path of the file");
				fin.close();
			}
			try {
				char* path = "case1.txt";//case1: S 1 2 3 4
				inputFile(path);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "Incorrect Num at line 1, the Num must be a positive integer");
				fin.close();
			}
			try {
				char* path = "case2.txt";//case2: 2    A 1 2 3 4    C 1 2 3
				inputFile(path);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "Incorrect type, correct types are L, S, R, C");
				fin.close();
			}
			try {
				char* path = "case3.txt";//case3: 2     R 1 2 3 4    C 1 aa 1
				inputFile(path);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "Incorrect parameter, please input integer and check the number of the circle parameters");
				fin.close();
			}
			try {
				char* path = "case4.txt";//case4: 2     C 1 2 3     R 1 2 1
				inputFile(path);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "Incorrect parameter, please input integer and check the number of the line parameters");
				fin.close();
			}
		}

添加直线错误：参数超出范围、起点终点重合、两线重合(无穷交点)

　　　　　　　　　TEST_METHOD(TestMethod23)
		{
			try {
				addLine("R", 1, 2, 3, 100000);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "parameter out of range, correct range is (-100000, 100000)");
			}
			
			try {
				addLine("R", 1, 1, 1, 1);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "two points coincide in a line definition,please input two different points");
			}
		}
　　　　　　　　　TEST_METHOD(TestMethod24) 
		{
			//直线和直线重合
			try {
				addLine("L", 1, 1, 2, 2);
				addLine("L", 3, 3, 4, 4);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "two lines coincide");
				lines.clear();
			}
			//射线与直线重合
			try {
				addLine("R", 1, 1, 2, 2);
				addLine("L", 3, 3, 4, 4);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "two lines coincide");
				lines.clear();
			}
			//射线与射线重合
			try {
				addLine("R", 1, 1, 2, 2);
				addLine("R", 3, 3, 4, 4);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "two lines coincide");
				lines.clear();
			}
			//射线与线段重合()
			try {
				addLine("R", 0, 0, 1, 1);
				addLine("S", 1, 1, -1, -1);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "two lines coincide");
				lines.clear();
			}
			//线段与直线重合
			try {
				addLine("S", 0, 1, 0, -1);
				addLine("L", 0, 0, 0, 2);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "two lines coincide");
				lines.clear();
			}
			//线段与射线重合
			try {
				addLine("S", 1, 1, -1, -1);
				addLine("R", 0, 0, 1, 1);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "two lines coincide");
				lines.clear();
			}
			//线段与线段重合
			try {
				addLine("S", 1, 1, 2, 2);
				addLine("S", 3, 3, 4, 4);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "two lines coincide");
				lines.clear();
			}
		}

添加圆错误：参数超出范围、半径小于0、与已有圆重合(无数交点)

　　　　　　　　　TEST_METHOD(TestMethod25)
		{
			try {
				addCircle(100000, 100000, -100000);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "parameter out of range, correct range is (-100000, 100000)");
			}
			try {
				addCircle(1, 2, -3);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "radius of circle must be a positive integer");
			}
			try {
				addCircle(1, 2, 3);
				addCircle(1, 2, 3);
			}
			catch (char* msg) {
				Assert::AreEqual(msg, "this circle exists");
			}
		}

九、界面模块的设计

为了实现几何图像的绘制，我们下载了并引入了C++图形库<graphics.h>，调用相应的库函数实现了draw()函数：

void draw() {
	COLORREF color = RGB(245, 245, 245);
	initgraph(Length, Height);
	setbkcolor(color);
	cleardevice();
	setlinestyle(PS_SOLID, 3); //调整画笔属性绘制坐标轴
	color = RGB(28, 28, 28);
	setlinecolor(color);
	line(0, Yaxis, Length, Yaxis);	//x轴
	line(Xaxis, 0, Xaxis, Height);	//y轴
	setlinestyle(PS_DASH, 1);
	color = RGB(156, 156, 156);
	setlinecolor(color);//调整画笔颜色，绘制网格
	for (unsigned int i = 0; i < Length / PerUnit; i++) {
		line(i * PerUnit, 0, i * PerUnit, Height);
		line(0, i * PerUnit, Length, i * PerUnit);
	}
	setlinestyle(PS_SOLID, 3);
	color = RGB(99, 184, 255);
	setlinecolor(color);//调整画笔属性，绘制圆
	for (unsigned int i = 0; i < circles.size(); i++) {
		Circle c = circles.at(i);
		circle((int)c.x * PerUnit + Xaxis, Yaxis - (int)c.y * PerUnit, (int)c.r * PerUnit);
	}
	color = RGB(255, 64, 64);
	setlinecolor(color);//调整画笔属性，绘制不同类型的直线(采用虚函数实现多态)
	for (unsigned int i = 0; i < lines.size(); i++) {
		lines.at(i)->draw();
	}

}

对于求解得到的交点，我们采用小圆的方式同样在图中绘出，并在控制台窗口同步显示出各点坐标的具体信息，告知用户求解结果：

void drawPoint() {
	setlinestyle(PS_SOLID, 3);
	COLORREF color = RGB(46, 139, 87);
	setfillcolor(color);
	setlinecolor(color);//调整画笔属性，绘制交点
	set<Point>::iterator iter = points.begin();
	FILE* fp = NULL;
	AllocConsole();//申请一个控制台用于展示结果
	freopen_s(&fp, "CONOUT$", "w", stdout);
	int i = 0;
	while (iter != points.end()) {
		i++;
		int x = (int)(Xaxis + iter->x * PerUnit);
		int y = (int)(Yaxis - iter->y * PerUnit);
		cout << "Intersect Point " << i << ": (" << iter->x << ", " << iter->y << ")" << endl;
		fillcircle(x, y, 3);//半径为3像素点的实心小圆
		iter++;
	}
	FreeConsole();
}

十、界面模块与计算模块的对接

我们本次项目的UI使用了VS中的MFC框架来实现，可以使用工具箱拖动添加控件的方式直接调整界面的布局，十分的方便，对于添加的按钮也只需双击即可自动跳转到其对应的响应函数，直接向其中添加所需执行的相应操作即可，也正是通过这一简单的按钮响应方式实现了对接口的调用，即模块的对接。在文本框中输入的内容可以通过定位文本框属性ID后调用GetDlgItemText()函数来获取，从而实现了与用户的信息交互。使用提示消息框MessageBox可以把操作成功信息或者所调用接口的异常信息反馈给用户，方便用户实时调整。

给出其中一个按钮(addLine)的响应部分代码，其余类似：

void CUIDlg::OnBnClickedButton4()
{
	// TODO: 在此添加控件通知处理程序代码
	try {
		CString ctype, cx1, cy1, cx2, cy2;
		GetDlgItemText(IDC_EDIT2, ctype);
		GetDlgItemText(IDC_EDIT3, cx1);
		GetDlgItemText(IDC_EDIT4, cy1);
		GetDlgItemText(IDC_EDIT5, cx2);
		GetDlgItemText(IDC_EDIT6, cy2);
		if (ctype.GetLength() == 0 || cx1.GetLength() == 0 || cy1.GetLength() == 0
			|| cx2.GetLength() == 0 || cy2.GetLength() == 0) {
			throw "type or parameters can not be NULL";
		}
		string type = c2s(ctype);
		string x1 = c2s(cx1);
		string y1 = c2s(cy1);
		string x2 = c2s(cx2);
		string y2 = c2s(cy2);
		if (type != "L" && type != "R" && type != "S") {
			throw "Line type must be L, R or S!";
		}
		if (!isDigit(x1) || !isDigit(y1) || !isDigit(x2) || !isDigit(y2)) {
			throw "parameters must be integer!";
		}
		addLine(type, (long long)stoi(x1), (long long)stoi(y1), 
			(long long)stoi(x2), (long long)stoi(y2));

		string str = "Add line succeed!";
		string cap = "Message";
		MessageBox((CString)str.c_str(), (CString)cap.c_str());
	}
	catch (const char* msg) {
		CString cmsg = s2c(msg);
		AfxMessageBox(cmsg);
	}
}

整体效果展示：

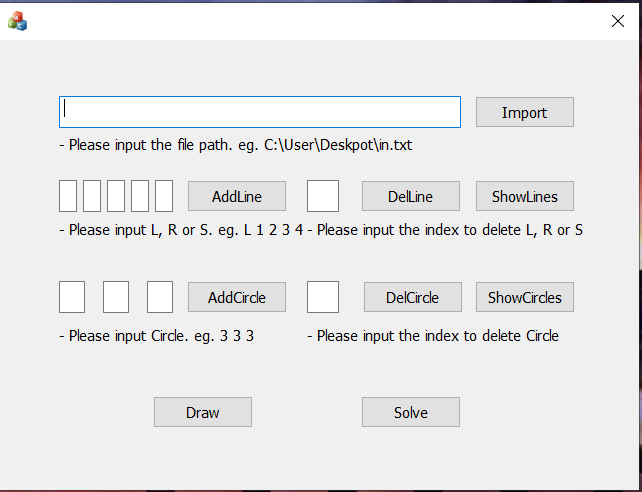
使用ShowLine和ShowCircle功能可以显示已存几何对象的在存储结构中的index信息，从而让用户输入index删除不想要的几何对象。

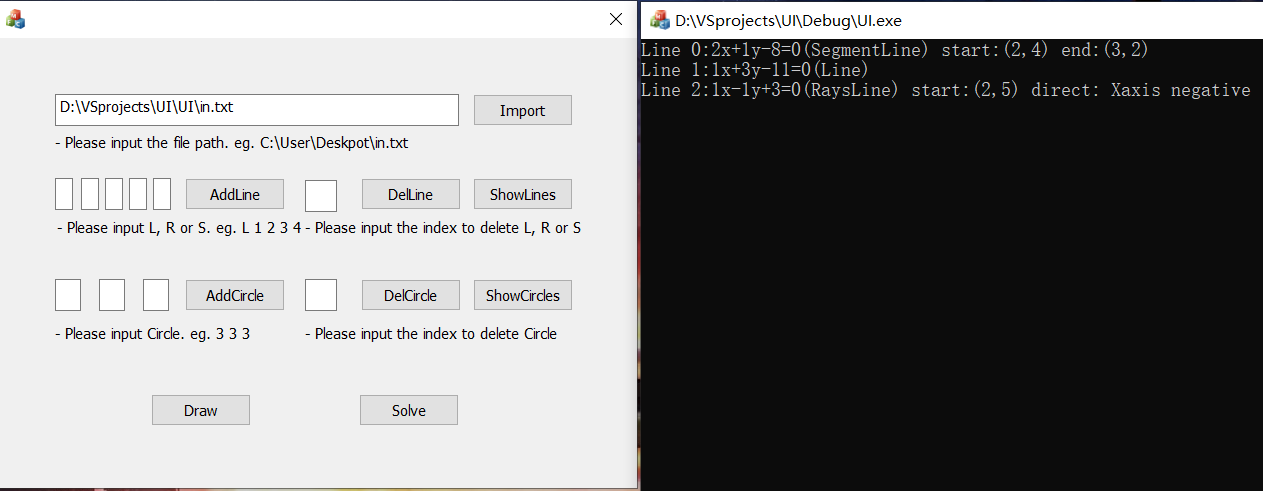
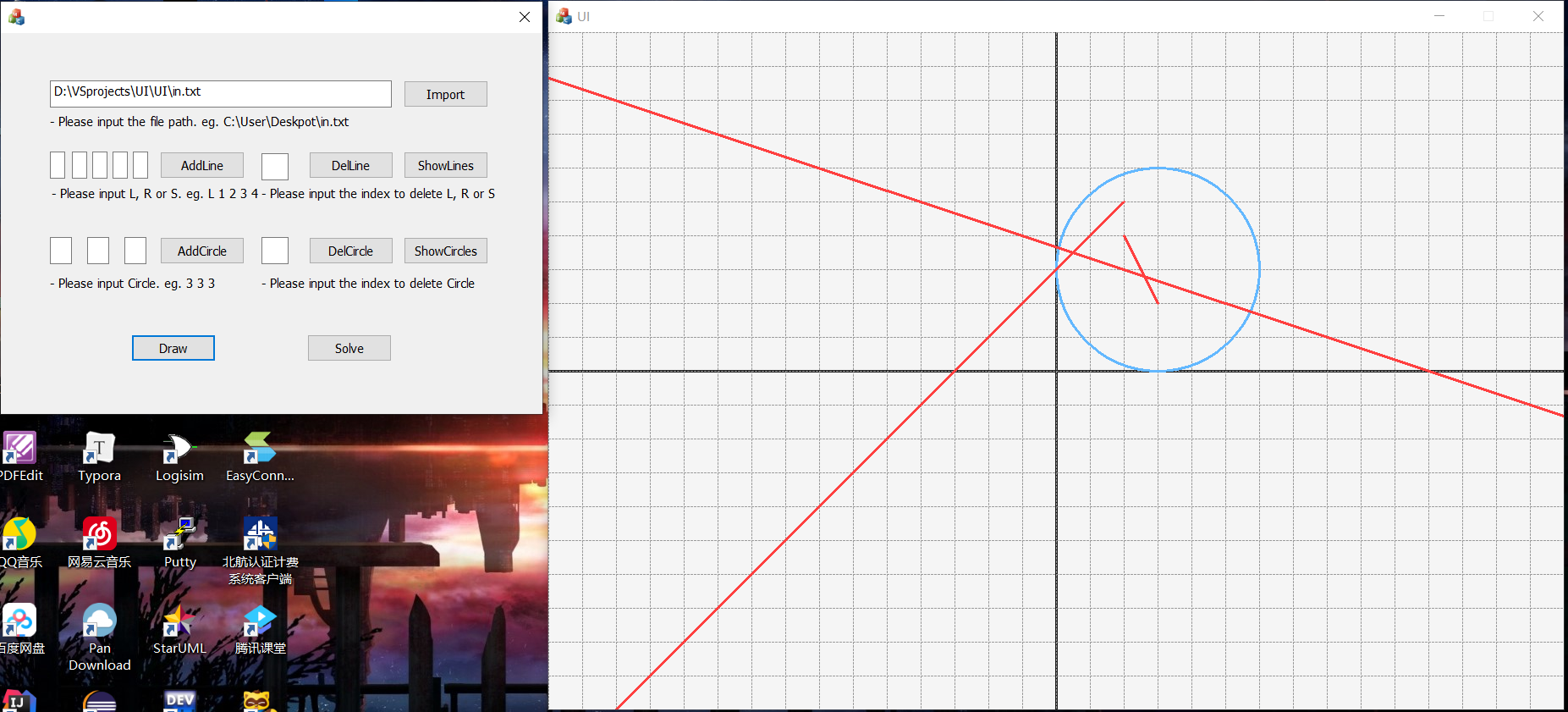
画图功能Draw:

求解功能Solve，同步显示交点坐标的具体信息:

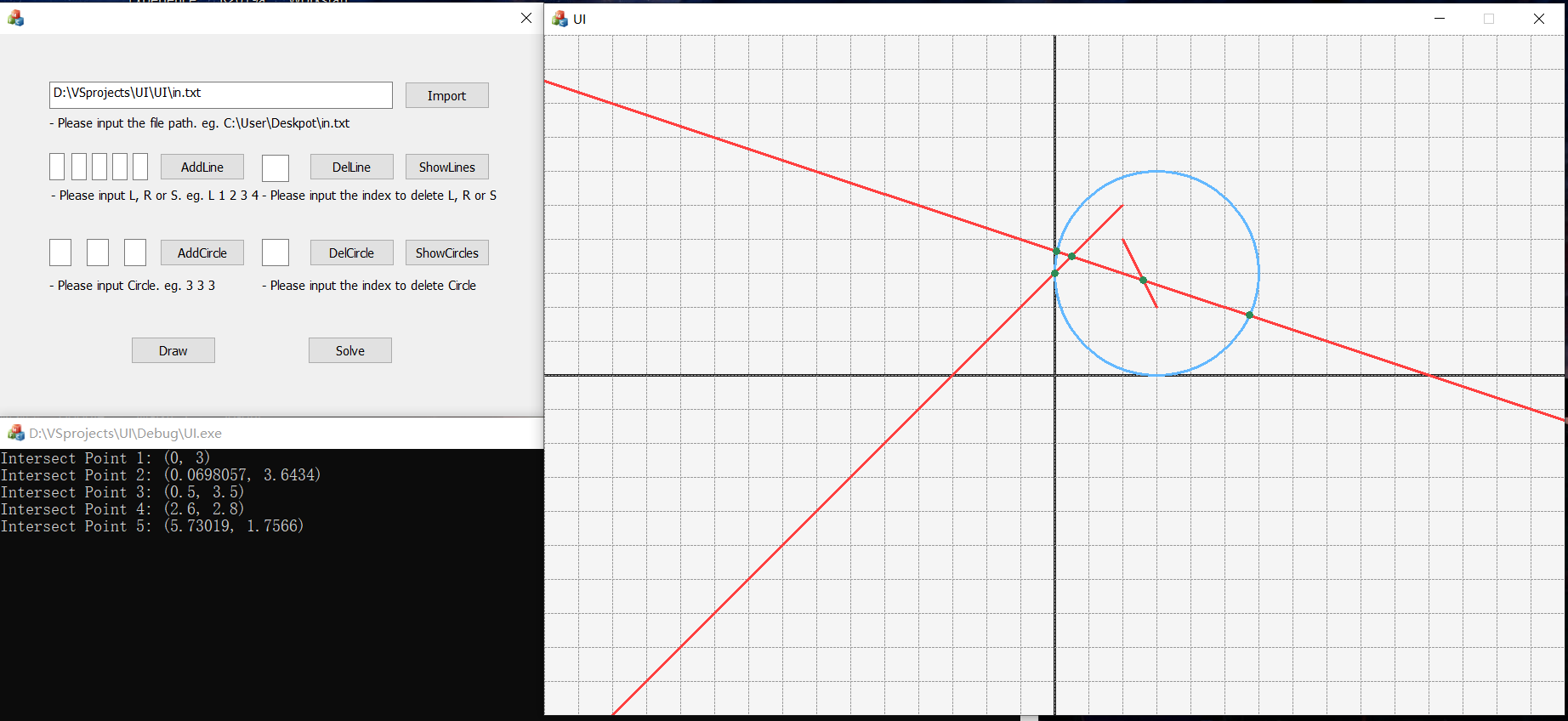
十一、结对编程过程展示

我和结对伙伴使用了QQ中的共享屏幕功能完成了结对编程：

十二、结对编程体会

结对编程的优点：

及时发现代码中的低级错误，提高工作效率。
两人相互监督，不容易懒惰，稳步推进工作进度。
两人掌握的知识相互补充，可以从多个方面思考并解决问题。

结对编程的缺点：

当两人水平差距较大时，可能会在交流上出现困难，较低水平者很难跟上较高水平者的思路。
意见不统一时容易持续争执，定不下一个结果，浪费时间。

结对成员优缺点：

	优点	缺点
我	逻辑架构清晰；编程基础较好；学习新知识能力强	表达能力有所欠缺
结对伙伴	代码风格规范；理解能力强；善于表达自身观点	不够细心

posted @ 2020-03-24 18:54 Miracle_dz 阅读(225) 评论(4) 编辑收藏举报

刷新页面返回顶部

Miracle_dz