个人项目作业

项目	内容
所属课程	2020年春季计算机学院软件工程(罗杰 任健)
作业要求	个人项目作业
课程目标	切身参与完整的软件开发流程，积累专业技术知识和团队合作经验
本次作业实现方面	体验完整的项目开发流程，加深对于PSP的理解
教学班级	006(周五上午三四节)
项目地址	https://github.com/Miracle-dz/IntersectProject

一、PSP表格

PSP2.1	Personal Software Process Stages	预估耗时(分钟)	实际耗时(分钟)
Planning	计划
· Estimate	· 估计这个任务需要多少时间	20	20
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	60	60
· Design Spec	· 生成设计文档	20	15
· Design Review	· 设计复审 (和同事审核设计文档)	0	0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	10	10
· Design	· 具体设计	60	90
· Coding	· 具体编码	120	180
· Code Review	· 代码复审	45	75
· Test	· 测试（自我测试，修改代码，提交修改）	120	180
Reporting	报告
· Test Report	· 测试报告	20	15
· Size Measurement	· 计算工作量	20	15
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	50
	合计	525	710

二、解题思路描述

整个题目读下来，感觉是比较简单的平面几何问题，由于圆和直线的内容并不复杂，所以并没有去查阅太多数学方面的资料，整体的想法就是最简单的将每两个几何对象的方程联立，代入求解。反倒是在想实现代码的数据结构时费了些功夫，考虑到若两两联立，必然会导致出现在三个及以上的几何对象上的点被重复计数，这就需要进行存储时的判重处理，而且由于点的坐标只能使用浮点类型无法精确表示，故判断相等的方法和精度选择也十分重要，查阅了C++的各种STL，其中set和HashMap都能够实现高效的查询和判重，而对于自定义类型的set，需要重载小于运算符<保证查重时的判断，正好可以利用这一特点在重载方法中嵌入对于浮点数精度的判断，从而实现目的效果。

三、设计实现过程

• Point类：存储交点的浮点型坐标，重载<符号用于set并设置精度为1e-8的相等判断。

class Point {
public:
	double x;
	double y;

	Point(double x, double y) {
		this->x = x;
		this->y = y;
	}
	bool operator<(const Point& p) const {//使用自定义类型的set需要重载<运算符
		if (x < p.x && p.x - x > 1e-8) {
			return true;
		}
		else {
			if (fabs(x - p.x) <= 1e-8 && y < p.y && p.y - y > 1e-8) { //采用1e-8的精度判断相等
				return true;
			}
		}
		return false;
	}
};

• Line类：采用一般式Ax+By+C=0的形式存储读入的直线，声明了两个构造函数，第一个是由读入的两点计算一般式的三个参数，第二个则是直接给三个参数赋值。

class Line {
public://使用一般式表示直线，避免使用double出现精度损失。
	long long a;
	long long b;
	long long c;

	Line(long long x1, long long y1, long long x2, long long y2) {
		this->a = y2 - y1;
		this->b = x1 - x2;
		this->c = x2 * y1 - x1 * y2;
	}
	Line(long long a, long long b, long long c) {
		this->a = a;
		this->b = b;
		this->c = c;
	}
};

• Circle类：存储读入的圆，直接赋值圆心坐标和半径。

class Circle {
public:
	long long x;
	long long y;
	long long r;

	Circle(long long x, long long y, long long r) {
		this->x = x;
		this->y = y;
		this->r = r;
	}

• 存储结构：

vector<Line> lines;
vector<Circle> circles;
set<Point> points; //使用set保证同一点不被重复计数

• 单元测试的设计：
  1.对于重复交点的测试(即测试set功能是否保证消除重复)
  2.边界条件测试：
  -直线平行
  -直线相交
  -直线与圆相离
  -直线与圆相切
  -直线与圆相交
  -圆与圆相离(内含、外离)
  -圆与圆相切(内切、外切)
  -圆与圆相交(圆心在内or圆心在外)
  通过测试截图：
  

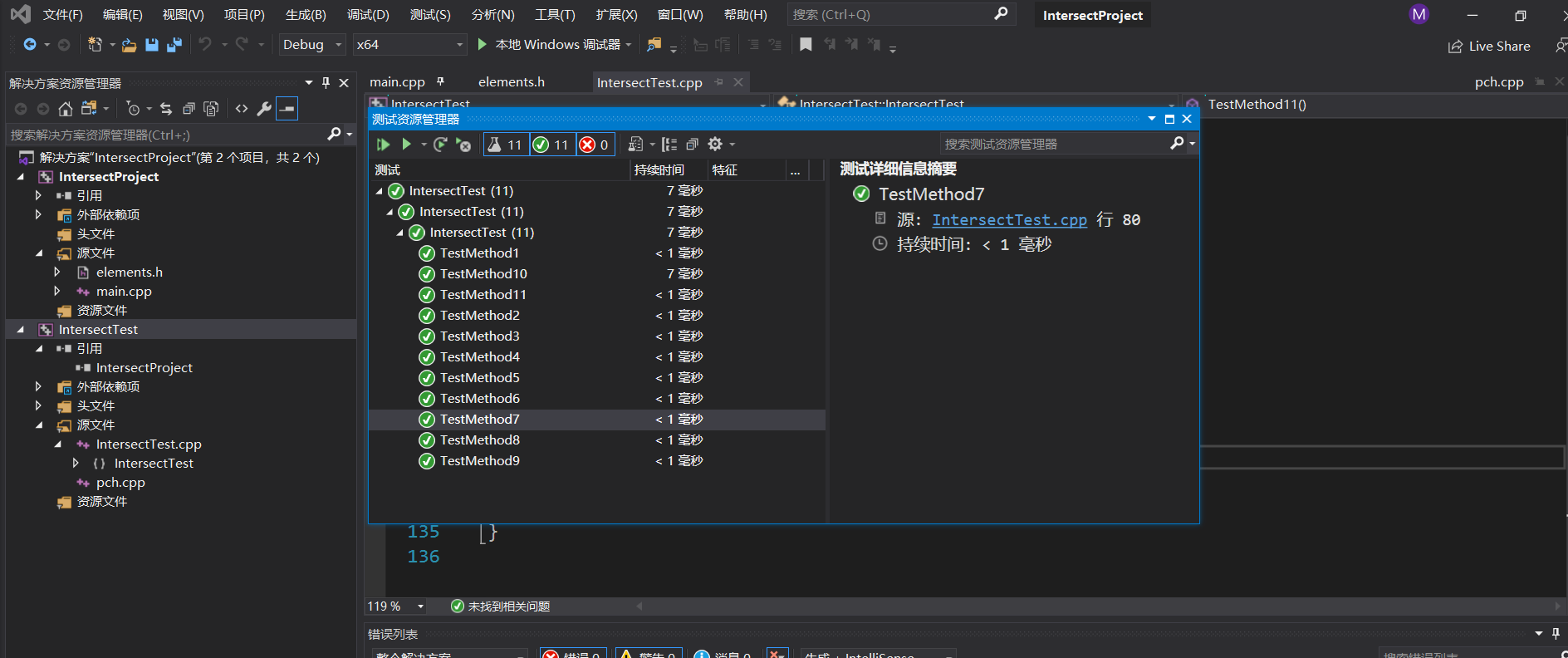
四、性能分析

(VS上的性能分析工具只显示一个函数，而没有下面各函数的具体细节，在群里求助老师同学也没有得到有效地解决，故只能手动分析，若后续找到有效的解决方法，会将相应图片和分析补全。)
通过和其他同学的交流讨论以及自己思考，可以得出整体的性能大部分花费到了set集合的insert操作上面，这其中就包含了对于重复节点的判断过程。在思考改进的方面考虑了换其他的数据结构如HashMap等，但是发现对于结点的出现次数并没有记录的必要，使用key-value对只是浪费空间和时间，阅读其他同学的博客时看到unsorted_set这一结构，其内部不像sort一样排序可以提高一些效率，我便去寻找了有关的一些资料，发现之所以set要重载小于运算符，正是因为要满足其内部的排序需求，而对于重复元素的判断则是进行一次小于判断后交换两元素的位置再进行一次小于判断，结果均为false时就判定为两者相等。而unsorted_set则是重载相等运算符，不需要受限于大小顺序，从而在每一次判重过程都少了一次比较。

五、代码说明

• 每两个几何对象联立求交点：

for (int i = 0; i < (int)lines.size(); ++i) {//直线与直线相交
		for (int j = i + 1; j < (int)lines.size(); ++j) {
			lineIntersectLine(lines[i], lines[j]);
		}
	}
	for (int i = 0; i < (int)lines.size(); ++i) {//直线与圆相交
		for (int j = 0; j < (int)circles.size(); ++j) {
			lineIntersectCircle(lines[i], circles[j]);
		}
	}
	for (int i = 0; i < (int)circles.size(); ++i) {//圆与圆相交
		for (int j = i + 1; j < (int)circles.size(); ++j) {
				circleIntersectCircle(circles[i], circles[j]);
			}
		}
	}

• 直线与直线联立：直接将化简得到的公式代入值

void lineIntersectLine(Line l1, Line l2) { 
	if (l1.b * l2.a != l1.a * l2.b) { //不平行才会相交
		double x = (double)(l2.c * l1.b - l1.c * l2.b) / (double)(l1.a * l2.b - l1.b * l2.a);
		double y = (double)(l2.c * l1.a - l1.c * l2.a) / (double)(l1.b * l2.a - l1.a * l2.b);
		Point p(x, y);
		points.insert(p);
	}
}

• 直线与圆联立：由直线解出y表示x，代入圆方程得y的一元二次方程，由判别式判断是否有交点并解出坐标；对于A为0时的直线，无法使用y表示x，直接将得到的y值代入圆得到x的一元二次方程求解。

void lineIntersectCircle(Line l, Circle cir) { 
	if (l.a == 0) { //水平线，直接得到y，再代入圆
		double y = -(double)l.c / (double)l.b; //将y值代入圆方程
		long long a = l.b * l.b;
		long long b = -2 * l.b * l.b * cir.x;
		long long c = l.c * l.c + 2 * l.b * l.c * cir.y + (cir.x * cir.x + cir.y * cir.y - cir.r * cir.r) * l.b * l.b;
		long long delta = b * b - 4 * a * c;
		if (delta > 0) {
			double x1 = (-b + sqrt(delta)) / (2l * a);
			double x2 = (-b - sqrt(delta)) / (2l * a);
			Point p1(x1, y);
			Point p2(x2, y);
			points.insert(p1);
			points.insert(p2);
		}
		if (delta == 0) {
			double x = (-b + sqrt(delta)) / (2l * a);
			Point p(x, y);
			points.insert(p);
		}
	}
	else {//直线Ax+By+C=0中A不为零，可以将x用y表示代入圆方程。
		long long a = l.a * l.a + l.b * l.b;
		long long b = 2 * (l.b * l.c + l.a * l.b * cir.x - l.a * l.a * cir.y);
		long long c = l.c * l.c + 2 * l.a * l.c * cir.x + (cir.x * cir.x + cir.y * cir.y - cir.r * cir.r) * l.a * l.a;
		long long delta = b * b - 4 * a * c;
		if (delta > 0) {
			double y1 = (-b + sqrt(delta)) / (2l * a);
			double y2 = (-b - sqrt(delta)) / (2l * a);
			double x1 = (-l.b * y1 - l.c) / l.a;
			double x2 = (-l.b * y2 - l.c) / l.a;
			Point p1(x1, y1);
			Point p2(x2, y2);
			points.insert(p1);
			points.insert(p2);
		}
		if (delta == 0) {
			double y = (-b + sqrt(delta)) / (2l * a);
			double x = (-l.b * y - l.c) / l.a;
			Point p(x, y);
			points.insert(p);
		}
	}

• 圆与圆联立：两圆方程相减得到过交点的直线方程，转为直线与圆交点问题。

void circleIntersectCircle(Circle c1, Circle c2) {
	if ((c1.x - c2.x) * (c1.x - c2.x) + (c1.y - c2.y) * (c1.y - c2.y) <= (c1.r + c2.r) * (c1.r + c2.r)//外切外交
		|| (c1.x - c2.x) * (c1.x - c2.x) + (c1.y - c2.y) * (c1.y - c2.y) >= (c1.r - c2.r) * (c1.r - c2.r)) {//内切内交
		long long a = 2 * (c1.x - c2.x);
		long long b = 2 * (c1.y - c2.y);
		long long c = c2.x * c2.x - c1.x * c1.x + c2.y * c2.y - c1.y * c1.y + c1.r * c1.r - c2.r * c2.r;
		Line l(a, b, c);
		lineIntersectCircle(l, c1);
	}
}

六、Code Quality Analysis分析并消除所有的警告