P5323 [BJOI2019]光线
Problem:
题目描述
当一束光打到一层玻璃上时,有一定比例的光会穿过这层玻璃,一定比例的光会被反射回去,剩下的光被玻璃吸收。
设对于任意 \(x\),有 \(x \times a_i\%\) 单位的光会穿过它,有 \(x \times b_i\%\) 的会被反射回去。
现在 \(n\) 层玻璃叠在一起,有 \(1\) 单位的光打到第 \(1\) 层玻璃上,那么有多少单位的光能穿过所有 \(n\) 层玻璃呢?
输入格式
第一行一个正整数 \(n\),表示玻璃层数。
接下来 \(n\) 行,每行两个非负整数 \(a_i,b_i\),表示第 \(i\) 层玻璃的透光率和反射率。
输出格式
输出一行一个整数,表示穿透所有玻璃的光对 \(10^9 + 7\) 取模的结果。
可以证明,答案一定为有理数。设答案为 \(a/b\) ( \(a\) 和 \(b\) 是互质的正整数),你输出的答案为 \(x\),你需要保证 \(a\equiv bx \space (\text{mod }10^9 + 7)\)。
样例 #1
样例输入 #1
2
50 20
80 5
样例输出 #1
858585865
样例 #2
样例输入 #2
3
1 2
3 4
5 6
样例输出 #2
843334849
提示
样例1解释:
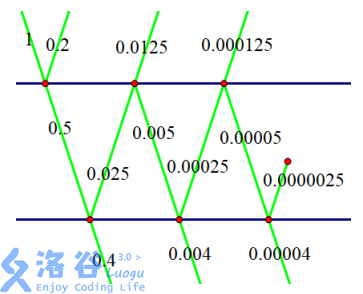
如图,光线从左上角打进来,有 \(0.5\) 单位的光穿过第 \(1\) 层玻璃,有 \(0.2\) 单位的光被反射回去。这 \(0.5\) 单位的光有 \(0.4\) 单位穿过第 \(2\) 层玻璃,有 \(0.025\) 单位的光被反射回去。这 \(0.025\) 单位的光有 \(0.0125\) 单位穿过第 \(1\) 层玻璃,有 \(0.005\) 单位的光被反射回去。这 \(0.005\) 单位的光有 \(0.004\) 单位穿过第 \(2\) 层玻璃……于是,穿过两层玻璃的光一共有\(0.40404... = 40/99\) 单位。在模 \(10^9+7\) 意义下等于 \(858585865\)。
数据范围:
对于 \(5\%\) 的数据,\(n=1\);
对于 \(20\%\) 的数据,\(n\le 2\);
对于 \(30\%\) 的数据,\(n\le 3\);
对于 \(50\%\) 的数据,\(n\le 100\);
对于 \(70\%\) 的数据,\(n\le 3000\);
对于 \(100\%\) 的数据,\(n\le 5\times 10^5\),\(1\le a_i \le 100\),\(0\le b_i \le 99\),\(1\le a_i+b_i \le 100\)。
每组 \(a_i\) 和 \(b_i\) 在满足上述限制的整数中随机生成。
Solution:
这是一道物理背景的题目,当然它的解法也非常物理。
作为一个初中蒟蒻,自然这题要用初三物理的方法了(
我们拿到题初看,觉得无从下手,因为这么多块玻璃,光线弹来弹去的,还不时会被吸收,令人头大。
那我们不妨先来探究特例,即 \(n=2\) 的情况。
使用样例中的图了。

观察到,光从第一层玻璃射入,穿透第二层玻璃分第一次机会,第二次机会,第三次机会 ...... 以至无穷。
第一次机会时有多少光能够穿透第二层玻璃呢?
很显然光需要先穿透第一层玻璃,再穿透第二层玻璃,那么根据乘法原理将有 \(a_1\%\times a_2\%\) 单位的光第一次机会穿过第二层玻璃。
第二次呢,观察到这回需要先穿透第一层玻璃,在第二层玻璃上反弹,再在第一层玻璃上反弹,再穿透第二层玻璃,故将有 $a_1%\times a_2%\times b_1%\times b_2% $ 单位的光第二次机会穿过第二层玻璃。
之后呢?
我们发现每一次都需要多在分别两块玻璃板上反弹一次,便会多乘上一个 \(b_1\%\times b_2\%\) 的系数,所以具体而言,对于第 \(k\) 次机会,会有 $a_1%\times a_2%\times (b_1%\times b_2%)^{k-1} $ 单位的光穿过第二层玻璃。
那么观察到所有机会中穿透的光之和是一个等比数列求和的形式,即 \(a_1\%\times a_2\%\times \sum\limits_{i=0}^{+\infty}(b_1\%\times b_2\%)=\frac{a_1\%\times a_2\%}{1-b_1\%\times b_2\%}\)。
后面的这个求和是等比数列求和公式在项数 \(k\) 趋于无穷以及公比 \(|p|<1\) 时的推广。
那么我们成功解决了 \(n=2\) 的问题!
如何推广?
考虑使用初中物理的一个重要方法,等效替代法!
我们是不是能将对于连续的多块玻璃看做一块玻璃呢?
对于连续的多块玻璃,其实我们没有必要了解其内部繁杂的反弹过程,相反,我们只记录我们需要的。
观察如果我们将多块玻璃看成了一块玻璃需要记录什么。
还是用这张图(

我们发现只需要记录从这多块玻璃中一束光射入最上方的玻璃最后从最下方的玻璃出来的光的多少以及一束光射入最下方的玻璃最后又从最下方的玻璃射出的光多少。
然后我们就可以递推了,我们设 \(A_i,B_i\) 表示将前 \(i\) 块玻璃当做一块玻璃时以上我们需要维护的两者。
每次我们将一块新的玻璃加入这多块玻璃中,并维护新的 \(A_i,B_i\)。
至于怎么维护?类似 \(n=2\) 的推导,较易,读者可以自行推导完成,不过多赘述。
#include<bits/stdc++.h>
using namespace std;
#define inf 0x7fffffff
#define timeused() (double)clock()/CLOCKS_PER_SEC
#define rep(i,a,b) for(register int i=a,i##end=b;i<=i##end;++i)
#define repp(i,a,b) for(register int i=a,i##end=b;i>=i##end;--i)
#define mp make_pair
#define pb push_back
#define mod 1000000007
typedef long long ll;
typedef unsigned long long ull;
template<typename T> inline T rd(T& x){
T f=1;x=0;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(T)(c-'0');
x*=f;
return x;
}
ll qp(ll b,ll p){
ll ans=1,base=b;
while(p){
if(p&1) ans=ans*base%mod;
base=base*base%mod;
p>>=1;
}
return ans;
}
ll a[500005],b[500005],n;
int main(){
rd(n);
rep(i,1,n){
rd(a[i]);
a[i]=a[i]*qp(100,mod-2)%mod;
rd(b[i]);
b[i]=b[i]*qp(100,mod-2)%mod;
}
rep(i,2,n){
ll nwa,nwb;
nwa=nwb=0;
nwb+=b[i];
nwb+=a[i]*a[i]%mod*b[i-1]%mod*qp(((1-b[i]*b[i-1])%mod+mod)%mod,mod-2)%mod;
nwb%=mod;
nwa+=a[i-1]*a[i]%mod*qp(((1-b[i]*b[i-1])%mod+mod)%mod,mod-2)%mod;
nwa%=mod;
a[i]=nwa;
b[i]=nwb;
}
printf("%lld",a[n]);
}


