[POI2014]DOO-Around the world

通过几年的努力，Byteasar最终拿到了飞行员驾驶证。为了庆祝这一事实，他打算买一架飞机并且绕Byteotia星球赤道飞行一圈。但不幸的是赤道非常长所以需要中途加几次油。现在已知赤道上面所有飞机场，所有飞机从飞机场起飞降落也可以加油。因为买飞机是个十分重大的决定，Byteasar决定寻求你的帮助。他将会让你模拟不同的飞行路线。自然这些飞机一次能走的航程是不同的。对于每次模拟，他想要知道最少需要降落多少次（包括最后一次）。需要注意的是起点可以任意选取。

 

询问<=100,飞机场<=1e6

O（1e8）可过。

 

断环成链，复制一倍。

假设出发点都在[n+1,n+n]，往左走。（即逆时针）

fa[i]表示i起点，终点在哪里（可能不是真正的终点）

dp[i]表示，i到终点fa[i]的最少步数。

那么，每次找到能走的最远的j，fa[i]=fa[j],dp[i]=dp[j]+1

然后出现i-fa[i]>=n的情况，直接输出dp[i]

 

原因：

首先这样可以遍历所有的出发点，可以遍历到最优解。

即使fa[i]开始并不是真正的终点，但是可以在后面枚举到。

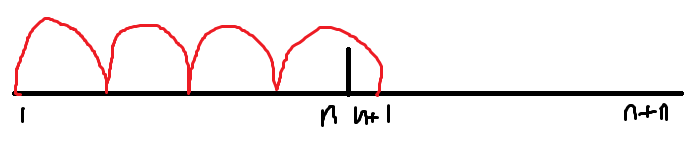
假如n+1开始的解是这样。

我们开始枚举n+1的第一步能跳的。于是n+1的终点是：

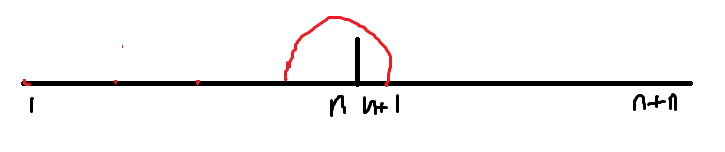
但是上面的情况也能枚举到。由于是一个环，所以在后面的部分会枚举到这种情况。

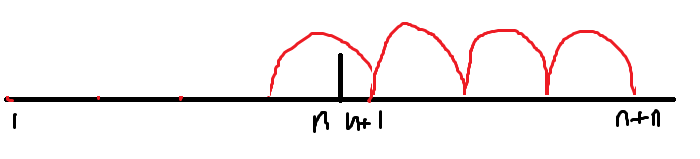
就像这样。

本质是同一种情况。

 

为什么可以直接退出？

因为如果当前满足的话，不存在一个更靠后的位置，使得比dp[pos]还大。

如果存在，一定会出现这种情况：

绿色这里，蓝色决策直接跨过了红色的一段。因为红色找的是最远 的能跳的，所以这样肯定是不合法的。

 

 

代码：

#include<bits/stdc++.h>
#define ri register int
using namespace std;
typedef long long ll;
const int N=1000000+5;
int n,s;
int fa[2*N],dp[2*N],sum[2*N];
int main(){
    scanf("%d%d",&n,&s);int x;
    int mx=0;
    for(ri i=1;i<=n;++i){
        scanf("%d",&x);
        mx=max(mx,x);
        fa[i]=i;
        sum[i]=sum[i-1]+x;
    }
    for(ri i=n+1;i<=n+n;++i) sum[i]=sum[i-1]+sum[i-n]-sum[i-n-1];
    while(s--){
        int d;scanf("%d",&d);
        if(d<mx) printf("NIE\n");
        else
        for(ri i=n+1,j=1;i<=n+n;++i){
            while(sum[i]-sum[j]>d) ++j;
            dp[i]=dp[j]+1;
            fa[i]=fa[j];
            if(i-fa[i]>=n){
                printf("%d\n",dp[i]);break;
            }
        }
    }return 0;
}