AGC 018E.Sightseeing Plan——网格路径问题观止
鸣谢:AGC 018E.Sightseeing Plan(组合 DP)
本蒟蒻认为,本题堪称网格路径问题观止。
因为涵盖了不少网格路径问题的处理方法和思路。
一句话题意:
给你三个矩形。
三个矩形从左下到右上排开。矩形顶点坐标范围是1e6
- 1≤X1≤X2<X3≤X4<X5≤X6≤106
- 1≤Y1≤Y2<Y3≤Y4<Y5≤Y6≤106
大概就是这样:
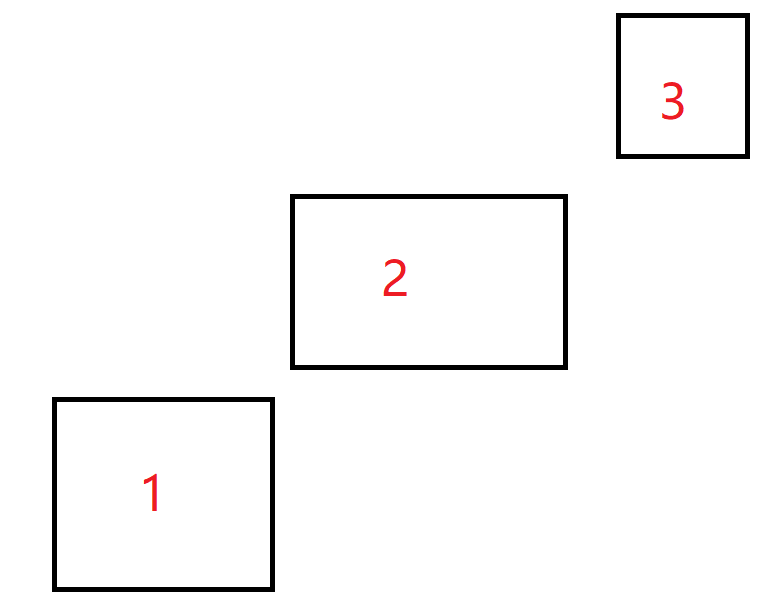
对于所有的1中选择一个点P1,2中选择一个点P2,3中选择一个点P3。
求从P1到P2再到P3的最短路径条数之和。
从一个矩形再到另外一个矩形还要经过一个矩形太复杂。我们化简情况处理下。
反正本质就是所有三个点之间的路径。
一、一个点到一个点
你必须要知道的:
从(x1,y1)到(x2,y2)的最短路径,就是只能往上或者往右走。
最短路径条数就是:C(x2-x1+y2-y1,x2-x1)
所以我们可以O(1000000^6)枚举
二、一个点到一个矩形
$F(x,y)$表示,从$(0,0)$到$(x,y)$的路径条数。
这个可以直接算。
发现,
$F(x,y)=\sum_{j=0}^yF(x-1,j)$
可以理解为,从原点到所有的$(x-1,j)$然后向上走一步,然后直接向右到达$(x,y)$
肯定不重不漏。
那么,可以得到:
从$(0,0)$到一个矩阵路径,就是:
$F(x2+1,y2+1)-F(x2+1,y1)-F(x1,y2+1)+F(x1,y1)$
就是一个小容斥。
用上面的$F(x,y)=\sum_{j=0}^yF(x-1,j)$
把$F(x2+1,y2+1)$还有$F(x1,y2+1)$展开消一消,
每次保留$F(x2+1,j)$和$F(x1,j)$往下消。
画画图就看出来了。
所以,我们得到了从一个点到一个矩阵的路径条数。
只要计算那四个点即可。
三、一个矩形到一个矩形
列出式子:
$G$示路径条数
$M_1$代表第一个矩形,$M_2$代表第二个矩形。
$\sum_{x1} \sum_{y1} \sum_{x2} \sum_{y2}G((x1,y1),(x2,y2))$
可以提出两个sigma
变成枚举一个点,求到另外一个矩形的方案数
$\sum_{x1} \sum_{y1}G((x1,y1),M_2)$
其实就是:
$\sum_{x1} \sum_{y1}\sum_{xx}\sum_{yy}(G((x1,y1),(xx,yy))$
$xx,yy$代表那四个关键点。(省略了四个关键点正负号)
反过来,每个关键点都会被$M_1$所有的点统计一次。
所以,一个关键点的贡献,就是这个关键点到$M_1$的路径条数。
就是这个关键点到$M_1$的四个关键点路径条数。(当然,要有正负号)
所以,一个矩形到一个矩形的路径条数,
就是两个矩形四个关键点分别进行条数计算。处理好符号即可。
四、一个矩形经过一个矩形再到另一个矩形
可以把三的结论推广。
就是,第一个矩形四个关键点,到第三个矩形四个关键点,然后路径上经过第二个矩形的方案数。
所以,$4\times 4$枚举第一第三个矩形的关键点的话,
问题就变成了从一个点出发,经过一个矩形再到另外一个点的方案数。
直接枚举还是$O(n^2)$的。
发现,经过第二个矩形,
必然要么从$(x,y3)$(下边界)要么从$(x3,y)$(左边界)
进入。
所以,我们枚举进入点。
进入这个点,就一定进入了这个矩形。再到终点的任意一条路径,都是合法的。
再乘上从起点到这个进入点的方案数就是这个进入点的贡献。
必然不重不漏地枚举完了所有的合法路径。
所以我们成功的A掉了这个题。
五、然鹅并没有做完。。。
发现,不是要求经过第二个矩形的路径条数啊,我们要在第二个矩形中选择一个点。。。。
一个经过第二个矩形的长度为$len$的路径,就对应着$len$个方案。(每个位置都可以作为$P_2$)
我们经常转化研究对象,尝试分开统计贡献。
分开统计的前提是,贡献必须可以处理成互不相关的形式。
这个可以不可以呢?
但是凉凉,这个$len$还和离开点有关。。。
难道只能$O(n^2)$枚举进入点和离开点?
不!我们还有方法!
一个$len$怎么计算?
进入点$(x1,y1)$,离开点$(x2,y2)$
有$len=x2-x1+y2-y1+1$
诶!!
$x1,x2,y1,y2$貌似可以分离!!
那么,我们可以枚举进入点。
贡献是:$(-1)\times$刚才的两个组合数$\times(x+y)$
离开点:
贡献是:$(+1)\times$刚才的两个组合数$\times(x+y)$
(其实这个也是不重不漏枚举了所有路径)
相加的话,
发现,对于每个合法的路径,恰好被计算了两遍。(进入离开点各一次)
第一遍把$-x1-y1$算上,
第二遍把$x2+y2+1$算上。
所以,每个合法路径贡献就是$len$次。和题意符合。
完结撒花!!!~~~
六、一些代码实现细节:
1.len的长度是:$(x2-x1+y2-y1+1)$别忘了$+1$
2.注意,矩阵矩阵的之间的路径,
根据推导,是先转化成$M_2$中关键点到$M_1$矩阵的路径,所以,$M_1$的矩阵的四个关键点分别是$(x1-1,y1-1),(x2,y1-1),(x1-1,y2),(x2,y2)$
类比之前,这个是从上往下走的,所以要这样处理。
#include<bits/stdc++.h> #define ri register int using namespace std; typedef long long ll; const int mod=1e9+7; const int N=2e6+3; ll ans=0; ll jie[N],ni[N]; struct node{ int x,y,fl; void init(int a,int b,int c){ x=a,y=b,fl=c; } }p[20]; int tot; int x3,y3,x4,y4; int xx[10],yy[10]; ll qm(ll x,ll y){ ll ret=1; while(y){ if(y&1) ret=ret*x%mod; x=x*x%mod; y>>=1; } return ret; } ll C(int n,int m){ return jie[n]*ni[m]%mod*ni[n-m]%mod; } ll G(int x1,int y1,int x2,int y2){ ll A=abs(x2-x1),B=abs(y2-y1); return C(A+B,B); } ll sol(int x1,int y1,int x2,int y2,int f1,int f2){ ll ret=0; for(ri x=x3;x<=x4;++x){ ret=(ret+G(x1,y1,x,y4)*G(x,y4+1,x2,y2)%mod*(x+y4+1))%mod;//注意这里的x+y4+1的+1 ret=(ret-G(x1,y1,x,y3-1)*G(x,y3,x2,y2)%mod*(x+y3)%mod+mod)%mod; } for(ri y=y3;y<=y4;++y){ ret=(ret+G(x1,y1,x4,y)*G(x4+1,y,x2,y2)%mod*(x4+y+1))%mod; ret=(ret-G(x1,y1,x3-1,y)*G(x3,y,x2,y2)%mod*(x3+y)%mod+mod)%mod; } ret=ret*(f1*f2); return ret; } int main(){ int x,y; for(ri i=1;i<=6;++i)scanf("%d",&xx[i]); for(ri i=1;i<=6;++i)scanf("%d",&yy[i]); jie[0]=1; for(ri i=1;i<=N-2;++i) jie[i]=jie[i-1]*i%mod; ni[N-2]=qm(jie[N-2],mod-2); for(ri i=N-3;i>=0;--i) ni[i]=ni[i+1]*(i+1)%mod; x3=xx[3],y3=yy[3],x4=xx[4],y4=yy[4]; p[1].init(xx[1]-1,yy[1]-1,1);p[2].init(xx[2],yy[1]-1,-1);//注意这里是这样的 p[3].init(xx[1]-1,yy[2],-1);p[4].init(xx[2],yy[2],1); p[5].init(xx[5],yy[5],1);p[6].init(xx[6]+1,yy[5],-1); p[7].init(xx[5],yy[6]+1,-1);p[8].init(xx[6]+1,yy[6]+1,1); for(int i=1;i<=4;++i){ for(int j=5;j<=8;++j){ ans=(ans+sol(p[i].x,p[i].y,p[j].x,p[j].y,p[i].fl,p[j].fl)+mod)%mod; } } printf("%lld",ans); return 0; }
七、总结
我们成功地把一个O(n^6)变成了O(n)
思路就是化简问题,然后从简单到困难,利用之前的结论考虑,不断转化简化问题。
最后的差分len也是异常精彩。
组合数和路径条数的问题,经常是考虑一个物品的贡献。
可以尝试往这方面想。
这里也有有一个不错的路径组合意义转化题:fzyzojP3782 -组合数问题


 浙公网安备 33010602011771号
浙公网安备 33010602011771号