根号算法——暴力美学

 

零、前言

• 根号算法是一种很常见的算法
• 常见的根号思想有：双向搜索、根号分类讨论、根号重建、复杂
度平衡，以及一些根号级别的数据结构如分块和莫队
• 这些算法一般是多种暴力算法的结合，一般具有较低的思维难度
和编码难度

 

——ImmortalCO猫

 

有的时候，我们可以对一个题想出两个暴力，各有各自的长处和短处。

如果我们能对数据范围进行分块处理，或者两个暴力分别算之后拼接在一起，就用两个合在一起的暴力，实现了正解。

通常这个分界点可以取到$\sqrt{n}$

所以叫根号算法。

以下是例题：

 

一、序列（复杂度平衡）

• 给出一个序列
• 求一个最长的子序列，使得对于子序列的每一项，它与上前面的
每一项都等于它本身
• 𝑛, 𝑎𝑖 ≤ 10^5

 

题解：

即，我们要找到一个子序列，使得后面的是前面的子集。

每个数写成2进制数有18位。

外层循环i从n~1

一个暴力是：枚举到当前的位置的时候，设f[S]表示，当前子序列并起来是S集合的最长长度。转移要枚举ai的子集。

转移O(2^18)（枚举子集），更新O(1)（就取个max）2^18*n TLE

还有一个暴力是：枚举到当前的位置的时候，设g[S]表示，如果这个时候所选择的并集是S的话，最长长度是多少。

转移O(1)（直接找g[ai]），更新O(2^18)（要找所有ai的超集尝试更新g）2^18*n TLE

我们发现，这两个暴力明显转移和更新的复杂度相差太多。而且恰好可以互补。

而且，因为就是一个求并集子集，所以一个数的每一位可以分开考虑，

所以，一个自然的想法是：

设dp[S1][S2]表示，前9位并集之后是S1，且如果并集后9位是S2的话，最长的长度是多少。

所以，我们的转移O(2^9)（枚举ai前9位的子集），更新O(2^9)（枚举ai后9位的超集）

即可达到复杂度平衡。

 

这个模型以后可能还会见到。

 

二、能量石（根号分类讨论）

（根号分类讨论
• 根号分类讨论是一种结合暴力的思想
• 它基于这样一个事实：如果某个种类的元素很多，那么这样的种
类一定不会太多
• 如果我们可以设计“基于种类元素的暴力”和“基于全局考虑某个种
类”的暴力，那么我们就可以结合两个暴力获得好算法）

 

题目：
• 给出一张图，每个点有点权
• 支持加边、删边、改点权。询问有连边的点对的点权和的最大值
• 𝑛, 𝑚 ≤ 200000

 

加边删边还是比较容易维护，但是改点权就比较麻烦了。

如果暴力改的话，和点的度数是有关系的。

我们不希望度数大的点改点权的复杂度太大。

 

所以，我们可以按照点的度数分块。

度数大于根号n的点叫做大点，反之叫做小点。

所有的小点之间的连边，把点的权值之和放进一个大根堆里。

每个大点开一个大根堆，里面是和它相连的点的权值。（自己的权值不要放进去）

大点显然最多只有根号n个。

当然，为了删边和改点权方便，我们还要开（根号n）+1个懒惰删除堆当垃圾桶。

 

这里面，加入权值也要加入编号，以便查询是否已经删除。

加边：

①小点与小点，直接把这个两个点的权值加入堆里面。

②小点与大点，把小点的权值加入这个大点的堆里面。

③大点与大点，把两个大点权值都加入对方的堆里面。

删边：

①小点与小点，直接把这两个点的权值加入小点们的垃圾桶。

②小点与大点，把小点的权值加入大点的垃圾桶里面。

③大点与大点，把两个大点的权值加入对方的垃圾桶里面。

改点权：

①小点，暴力枚举所有的出边，把这些边都加入垃圾桶里面。

然后暴力枚举所有出边，把新的点权加上这些点的点权，然后加入小点之间的大根堆里面。

②大点，O(1)直接修改自己。然后，维护这个大点相邻的大点，把这些大点的垃圾堆里面加入这个大点的旧点权，这些大点的堆里面加入这个新点权。

 

查询：

每次操作后，扫一遍所有的堆，如果某堆顶和垃圾桶堆顶一样，那么找下一个。

对于大点的堆，最大的没有删除的点权+自己点权构成备选答案。

所有答案取max，根号n时间。

注意重建：
可能一个小点经过若干次变成了一个大点，就要暴力重建一个大点。

为了避免麻烦，不妨当一个小点变成2sqrtn的度数的时候，再把这个点变成大点。

当一个大点的度数小于sqrtn的时候，变成小点。

 

O(nsqrt(n)logn)

 

三、light（关于模数的根号分类讨论）

9.22模拟赛

T3

 

四、雅加达的摩天大楼（关于步数的根号分类讨论）

Description

 印尼首都雅加达市有 N 座摩天楼，它们排列成一条直线，我们从左到右依次将它们编号为 0 到 N−1。除了这 N 座摩天楼外，雅加达市没有其他摩天楼。

有 M 只叫做 “doge” 的神秘生物在雅加达市居住，它们的编号依次是 0 到 M−1。编号为 i 的 doge 最初居住于编号为 Bi 的摩天楼。每只 doge 都有一种神秘的力量，使它们能够在摩天楼之间跳跃，编号为 i 的 doge 的跳跃能力为 Pi （Pi>0）。

在一次跳跃中，位于摩天楼 b 而跳跃能力为 p 的 doge 可以跳跃到编号为 b−p （如果 0≤b−p<N）或 b+p （如果 0≤b+p<N）的摩天楼。

编号为 0 的 doge 是所有 doge 的首领，它有一条紧急的消息要尽快传送给编 号为 1 的 doge。任何一个收到消息的 doge 有以下两个选择:

跳跃到其他摩天楼上；

将消息传递给它当前所在的摩天楼上的其他 doge。

请帮助 doge 们计算将消息从 0 号 doge 传递到 1 号 doge 所需要的最少总跳跃步数，或者告诉它们消息永远不可能传递到 1 号 doge。

1≤N≤30000

1≤Pi≤30000

2≤M≤30000

Solution

1.注意审题。0号doge到1号doge不是0到1点~！（ImmortalCO翻译错了）

像是一个最短路。

但是，如果我们直接跑的话，还要记录当前是哪条狗。

当然不能这样跑。

我们不如对当前位置的狗枚举是否要交换到这个狗往后跳，跳多少步结束。直接枚举这个结束的节点。

这样的复杂度绝对太高。

对于能跳的步数比较少的狗会费时间很多。

但是，发现这些狗可能跳几步就到了下一个同样的能力的狗（前提是两个位置对步数P同余），不如就到这里停止就行了。节省一些边。

看来要对步数进行讨论，数据范围也支持分块。

对于能力大于sqrt的狗，直接跳，最多sqrt次，共产生NsqrtN条边。

对于能力小于sqrt的狗，枚举mod P的余数分类，同余类内从开始往后跳到下一个狗位置，对期间的点连边。

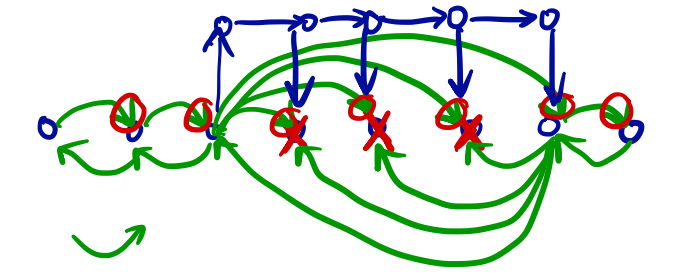
大概就是绿色的边。

边数是：sigma(k*N/k)=NsqrtN

然后跑spfa即可。

为了节省时空，可以在spfa内直接枚举边。

可以不用提前建好。