圆——高精无理数的处理

圆
• 在第一象限中依次画圆
• 第一个圆半径为 𝑅 且和两坐标轴相切
• 接下来每一个圆和前一个圆以及两个坐标轴相切
• 求第 𝑛 个圆的半径（保留整数部分末尾1000位）

• 𝑛 ≤ 10^18, 𝑅 ≤ 10^9

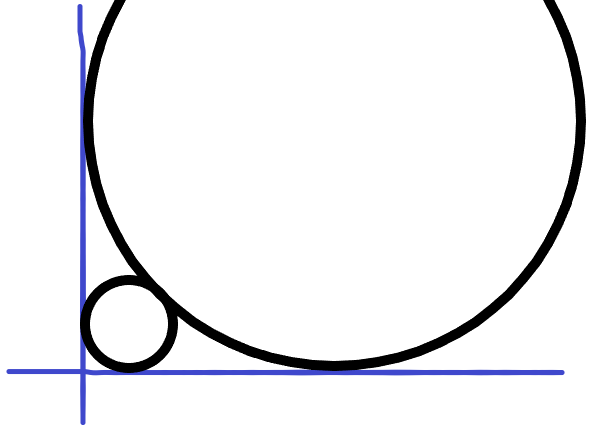
就是这样。

 

题解：

肯定要想通过递推公式处理一下通项公式。然后尝试快速幂

可以得到：$R_n=(3+2\sqrt{2})^n\times R$

无理数小数点怎么处理？保留整数但是要乘R，（<=1e9）所以要保留小数点后9位。

直接算的话，肯定要爆精度的。因为1e-10还是会影响到答案的，不能直接舍去。

问题点在于处理精度误差。

但是，我们可以奇技淫巧一下：

令$N=(3+2\sqrt{2})^n+(3-2\sqrt{2})^n$

那么，这个N一定是整数，因为无理数项都会消去。

我们可以求一个数对：$(a,b)=(a+b\sqrt{2})$

在平方中只会出现$\sqrt{2}$

所以，这个(a,b)可以自定义乘法，通过矩阵乘法求解。

 

然后我们要计算$N-(3-2 \sqrt{2})^n$还要注意小数点

令$t=(3-2\sqrt{2})^n$

即：$ans=N\times R - t\times R$

那么，如果用double，这里的t能保证9位数的精度吗？

t本身是小于1的，

乘上n次，几乎就是0了。

所以，在没来得及爆精度的情况下，t就几乎变成0了，这样，如果t*R几乎为0，N要下取整，所以，$ans=N-1$

所以，直接再暴力用double算一遍$t$，然后乘上R减去，下取整即可。

 

值得注意的技巧：

1.有序数对(a,b)的做法

2.$N=(3+2\sqrt{2})^n+(3-2\sqrt{2})^n$的转化，利用$(3-2\sqrt{2})<1$，从而使得要么变成0，要么在double可以承受的范围下。