CF757E Bash Plays with Functions

题解

q<=1e6，询问非常多。而n，r也很大，必须要预处理所有的答案，询问的时候，能比较快速地查询。

离线也是没有什么意义的，因为必须递推。

先翻译$f_0(n)$

$f_0(n)=\sum_d|n[(d,\frac{n}{d})=1]$

一个数的约数和约数的另一半互质，那么，必须意味着，对于n的每个质因子，要么全在d，要么全在n/d否则就不互质了，就是0

对于互质时，每个质因子有两种选择情况，

所以，f0就是$2^m$其中，m是n的质因子种类数。

 

然后还要处理fr的递推式。

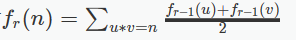
发现，还是和n的约数有关，反过来考虑每个约数的贡献，发现每个约数会被计算两次，u,v各一次

而还要除以2，正好消掉

那么，其实$f_r(n)=\sum_{d|n}f_{r-1}(d)$

这个是什么呢？$f_r(n)=f_{r-1}*1$（$*$表示卷积）

$f_0$是积性函数显然，

而卷积两侧是积性函数，那么卷积之后也是积性函数的。

所以，递推过去，$f_r$都是积性函数了。

所以，处理$f_r$可以把每个质因子分开考虑。

$f_r(n)=\Pi_{i=1}^k\space f_{r-1}(p_i^{q_i})$

$f_r(p_1^{q_1})=\sum_{d|{p_1^{q_1}}}f_{r-1}(d)=\sum_{k=1}^{q_1}f_{r-1}(p_1^{k})$

可以发现，如果递推到$f_0$的话，那么，就和质因子p1是什么，没有任何关系了。

所以，之后的取值，和p1是什么质因子，也没有关系。

只和p1的次数有关。

所以可以dp[i][j]第i层，次数为j的$f_i(j)$的值。

前缀和优化一下即可。

 

但是对于1e6次输入的数，怎么快速质因数分解呢？

假装你要线性筛素数，然后你可以顺便筛出mindiv（一个数的最小质因子）

然后，可以每次除掉mindiv，记录一下这个mindiv的次数。

即可利用mindiv，logn质因数分解

 

代码：

#include<bits/stdc++.h>
#define numb (ch^'0')
#define ri register int
using namespace std;
typedef long long ll;
const int N=1000000+5;
const int mod=1e9+7;
int q,r,n;
int pri[N],cnt;
int mindiv[N];
ll f[N][22],sum[22];
bool vis[N];
void rd(int &x){
    x=0;char ch;
    while(!isdigit(ch=getchar()));
    for(x=numb;isdigit(ch=getchar());x=(x<<1)+(x<<3)+numb);
}
void sieve(){
    mindiv[1]=1;//warning!!
    for(int i=2;i<=N-3;i++){
        if(!vis[i]){
            pri[++cnt]=i;
            mindiv[i]=i;
        }
        for(int j=1;j<=cnt;j++){
            if(pri[j]*i>N-3) break;
            vis[pri[j]*i]=1;
            mindiv[pri[j]*i]=pri[j];
            if(i%pri[j]==0) break;
        }
    }
}
int main(){
    sieve();
    f[0][0]=1;
    sum[0]=1;
    for(int i=1;i<=19;i++) f[0][i]=2,sum[i]=sum[i-1]+f[0][i];
    for(ri i=1;i<=N-3;i++){
        for(int j=0;j<=19;j++){
            f[i][j]=sum[j];
            sum[j]=0;
            if(j)sum[j]=sum[j-1];
            (sum[j]+=f[i][j])%=mod;
        }
    }
    int t;
    rd(t);
    while(t--){
        rd(r),rd(n);
        ll ans=1;
        while(n!=1){
            ll div=mindiv[n];
            int cnt=0;
            while(mindiv[n]==div) cnt++,n/=mindiv[n];
            (ans*=f[r][cnt])%=mod;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

/*
   Author: *Miracle*
   Date: 2018/10/3 22:15:15
*/

总结：

1.对于1e6的询问，必然要考虑探究性质，O(1)处理询问。

2.积性函数的证明:

①从实际意义考虑，如$f_0$

②直接理性证明，如$f_r$

这个是利用了卷积的性质

有时要考虑的是分开质因子能不能处理。