NOIP2017 列队——动态开点线段树
Description:
Sylvia 是一个热爱学习的女♂孩子。
前段时间,Sylvia 参加了学校的军训。众所周知,军训的时候需要站方阵。
Sylvia 所在的方阵中有n×m名学生,方阵的行数为 n,列数为 m。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中 的学生从 1 到 n×m 编上了号码(参见后面的样例)。即:初始时,第 i 行第 j 列 的学生的编号是(i−1)×m+j。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天 中,一共发生了 q件这样的离队事件。每一次离队事件可以用数对(x,y)(1≤x≤n,1≤y≤m)描述,表示第 x 行第 y 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达 这样的两条指令:
-
向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条 指令之后,空位在第 x 行第 m 列。
- 向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条 指令之后,空位在第 n 行第 m 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后, 下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 n 行 第 m 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以 Sylvia 想要计算每一次离队事件中,离队的同学 的编号是多少。
注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后 方阵中同学的编号可能是乱序的。
Hint

Solution
一年前暴力敲了30pts
一年后暴力敲了60pts
没什么长进啊
还是不会正解。
1.不懂树状数组
2.不想写平衡树
所以我们写动态开点线段树
首先发现,对于x=1的点,可以想到对这个链开一棵长度为max(n,m)+q的线段树。每次找第k个有数的地方,然后放到最后的位置。
发现,每次向前对齐只有最后一列要动,
向左看齐,只是当前的行会向左移动。
所以,为了便于操作,我们开n+1棵线段树,前n棵维护i行,1~m-1的答案
最后一棵n+1,维护最后一列n个答案。
然后我们就得到了一个优秀的MLE做法辣!~~
所以就要动态开点线段树。
(因为我比较弱)所以简单讲解一下动态开点线段树。
发现,有的时候,线段树需要维护的区间很大很大,但是实际用到的节点很少很少。
那么,我们干脆就不要开这么多的节点,用到的时候再向内存要。
也就是说,我们建立了一棵残疾的线段树,缺少很多枝叶,但是绝对够用了。
画个图大概理解一下(虽然也不太对)
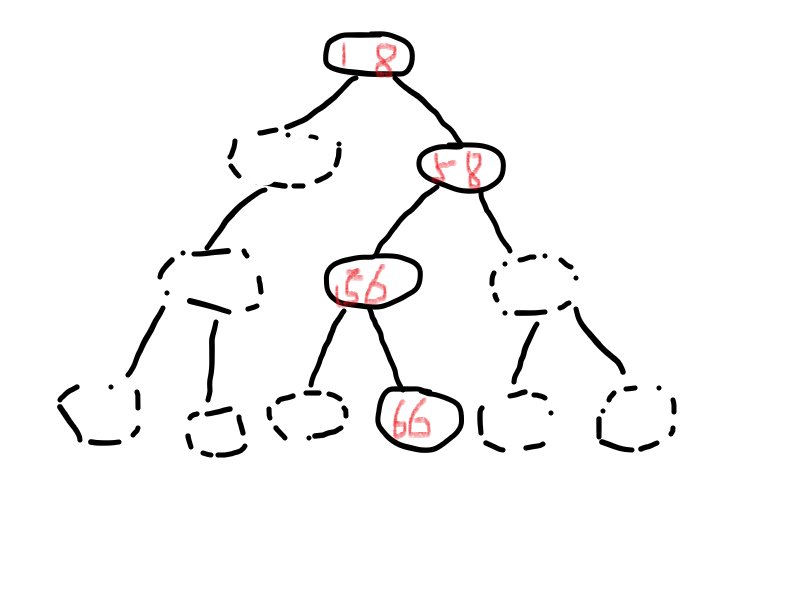
实心边框的点都是我们申请内存给的,虚的点是没用的。就算申请也不用,实在是浪费资源。
所以,
我们开局只有一个根,装备叶子全靠给。
例如我们要建立一个权值线段树,但是在线操作不让你离散化,值域又是inf级别的,
像这样,即使这个区间的范围很大,但是如果询问q比较少的话,我们只需要qloginf个节点,就可以办到。
(发现和主席树有点像,但是省空间的思想还是有些不同的。)
然后我们用动态开点线段树来做这个题。
线段树根节点维护的区间是max(n,m)+q;
开始每个线段树甚至连根也不用建,需要的时候会建起来。
每个线段树节点记录sz,子树实际的人数大小。(开始的时候,只有1~n(m-1)是sz=r-l+1的)
sz可以用一个函数处理。虽然并没有这么多的叶子,但是实际上,建出这么多的叶子,也是这个sz(这也是能动态开点的条件)
再记录一个val(long long型需注意),记录当前节点所代表的人的编号
这个编号val只有在叶子节点才有用。
其实每次询问引起的变化是:树x的第y个人走了,进入了树n+1的末尾,树n+1的第x走了,进入树x的末尾。
每次询问,如果y==m就进入线段树n+1查询,否则进入线段树x查询,找到答案ans输出
查询的时候,顺便sz--,删掉途经点的sz(就不用pushup了)
把ans这个编号放进n+1线段树的末尾(新开一个位置)
同样,途经sz++
如果y!=m说明,第x棵线段树最后进来一个人。就把n+1的第x个人查询(删除),放进线段树x的末尾(新开一个位置)。
这样子,其实每棵线段树根节点的sz都保持为m-1(或n)
Code
#include<bits/stdc++.h> #define mid ((l+r)>>1) using namespace std; typedef long long ll; const int N=3e5+5; const int M=1e7+2; ll n,m,q; struct node{ int ls,rs; int sz; ll val; }t[M]; int id,tot; int rt[N]; ll now; int cur[N]; int up; int get(int l,int r){ if(now==n+1){ if(r<=n) return r-l+1; if(l<=n) return n-l+1; return 0; } if(r<m) return r-l+1; if(l<m) return m-l; return 0; } ll query(int &x,int l,int r,int c){ if(!x){ x=++tot; t[x].sz=get(l,r); if(l==r){ if(now==n+1) t[x].val=l*m; else t[x].val=(now-1)*m+l; } } t[x].sz--; if(l==r) return t[x].val; if((!t[x].ls&&c<=get(l,mid))||c<=t[t[x].ls].sz) return query(t[x].ls,l,mid,c); else{ if(!t[x].ls) c-=get(l,mid); else c-=t[t[x].ls].sz; return query(t[x].rs,mid+1,r,c); } } void upda(int &x,int l,int r,int to,ll d){ if(!x){ x=++tot; t[x].sz=get(l,r); if(l==r){ t[x].val=d; } } t[x].sz++; if(l==r) return; if(to<=mid) return upda(t[x].ls,l,mid,to,d); else return upda(t[x].rs,mid+1,r,to,d); } int main() { scanf("%lld%lld%lld",&n,&m,&q); int x,y; ll ans; up=max(n,m)+q; while(q--){ scanf("%d%d",&x,&y); if(y==m) now=n+1,ans=query(rt[now],1,up,x); else now=x,ans=query(rt[now],1,up,y); printf("%lld\n",ans); now=n+1; upda(rt[now],1,up,n+(++cur[now]),ans); if(y!=m){ now=n+1; ans=query(rt[now],1,up,x); now=x; upda(rt[now],1,up,m-1+(++cur[now]),ans); } } return 0; }
upda:2018.11.2
感觉这个动态开点线段树其实不算是典型的动态开点23333
一般的线段树都是区间表示连续一些下标之类。动态开点也是如此。
但是这个做法的话,愣是把线段树写成了平衡树的存储方式。
区间的长度仅仅代表的是预留空间。
就是把许多点压成了一个点。


