概率和数学期望小结
概率：
1.一件事情发生的理论可能性。
2.∑pi=1
数学期望：
1.一件事情（随机变量）的取值结果和概率乘积的总和。
2.E(x)=∑pi*xi （期望定义）
3.E(ax+by)=aE(x)+bE(y) （期望的线性性质）
4.E(x*y)=E(x)*E(y)（x，y独立时一定成立）
例题1：
绿豆蛙的归宿
Description：
给出一个有向无环图，起点为1终点为N，每条边都有一个长度，并且从起点出发能够到达所有的点，所有的点也都能够到达终点。
绿豆蛙从起点出发，走向终点。 到达每一个顶点时，如果有K条离开该点的道路，绿豆蛙可以选择任意一条道路离开该点，并且走向每条路的概率为 1/K 。 现在绿豆蛙想知道，从起点走到终点的所经过的路径总长度期望是多少？
Solution：
基础期望。
f[i]:从i到n的期望长度。f[i]=1/k * ∑ ( f[ver[j]] + z[val[j]] ) j是边号。f[n]=0;
反向建边拓扑排序转移即可。
为什么是i到n？不是1~i？
1.因为，1~i设法，不能准确转移到f[ver[i]] , 因为1可能不会到i，期望长度没有意义。
2.因为，这样的转移，概率之和是决策点的度数倒数之和，可能不是1，转移无法解释。
------upda: 2023.6.15（对的，5年后来更新了）
f[i]表示1~i的也可以，但这个时候因为i不是每一次都到，对于不到的时候就没法统计了。
所以f[i]不能叫做“期望”，但f[i]仍然可以保存 所有从1开始走到i的路径的概率*对应的值 的和。也就是
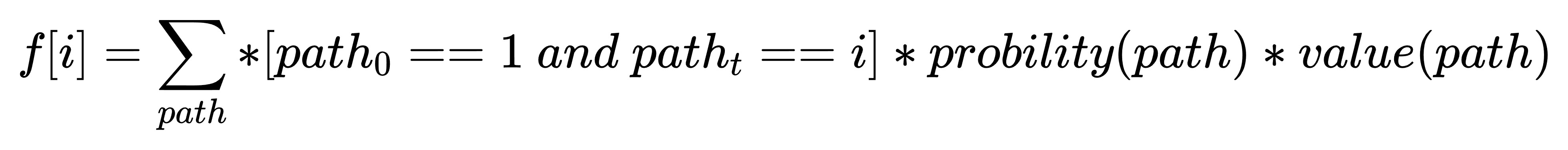
，然后也可以根据类似的式子进行dp转移。由于最后所有的路径最后都到f[n]，那么最后f[n]实际上就一定是一个“期望”了，也就是统计的所有路径的概率和为1。
例题2：
游走
Description：
一个无向连通图，顶点从1编号到N，边从1编号到M。 小Z在该图上进行随机游走，初始时小Z在1号顶点，每一步小Z以相等的概率随机选 择当前顶点的某条边，沿着这条边走到下一个顶点，获得等于这条边的编号的分数。当小Z 到达N号顶点时游走结束，总分为所有获得的分数之和。 现在，请你对这M条边进行编号，使得小Z获得的总分的期望值最小。
Solution：
首先进行贪心。经过次数最多的边赋值最小的编号。
转化为记录边的经过次数期望。不好算。
点的经过次数期望好算。p[i]=∑p[j]*1/d[j]
p[1]=∑p[j]*1/d[j] + 1
并且，因为到了n就停止了，所以与n有关的p[n]转移都不存在。
并且，p[n]=1;期望一定经过有且只有一次。
发现，无法递推。成环。
就列方程。高斯消元。
再求出经过边i的期望次数：l[i]=p[x]*1/d[x] + p[y]*1/d[y] （x，y两端点编号）
之后模拟就好。
例题3：
收集邮票：
例题4:
OSU!
Description：
一共有n次操作，每次操作只有成功与失败之分，成功对应1，失败对应0，n次操作对应为1个长度为n的01串。在这个串中连续的 X个1可以贡献X^3 的分数，这x个1不能被其他连续的1所包含（也就是极长的一串1，具体见样例解释）
现在给出n，以及每个操作的成功率，请你输出期望分数，输出四舍五入后保留1位小数。
N<=100000
xk[i]表示，到了i位置，连续有的1的个数的k次方的期望。
x1[i]=(x1[i-1]+1)*a[i]
x2[i]=(x2[i-1]+2*x1[i-1]+1)*a[i]
x3[i]=(x3[i-1]+3*x2[i-1]+3*x1[i-1]+1)*a[i]
x3[i]-x3[i-1]
答案数组：i位置期望得分
ans[i]=ans[i-1]+(3*x2[i-1]+3*x1[i-1]+1)*a[i];
答案是ans[n]
解释一下最后一行，如果第i位为1，答案增加的量是E((t[i-1]+1)^3)-E((t[i-1])^3)
计算的是增加量，否则难以快速计算这段1的开头位置。
增加量只有这么多，因为之前和ans[i-1]是一样的。
t[i]表示i往前有连续几个1
这是一个随机变量，不是期望值。
E(t[i])=x1[i]...
(update 2018.9.19)
例题5
noip 2016 换教室
线性期望dp的经典题目了。
此题关键在于弄清楚：E(x)=P(x)*x
例题6
不太正规的树形期望dp，和线性dp还有一些关联。
关键点在于状态设计和环形的线性处理。
例题7
SHOI2014，树形+二次扫描换根+期望dp
其实看似多了一个树形结构，但是树形结构性质优美，
树形dp也是比较有规律的。
例题8
[Noi2012]迷失游乐园
同样是：树形+二次扫描换根+期望dp
但是由于基环树的出现，分类讨论了，思维量就大多了。
总结：
数学期望以难以证明的性质，花样繁出的特点闻名于OI界。
其难以下手的恐惧，令不少蒟蒻心有余而力不足。
还是抓住关键的线性递推式，和期望定义 。 慢慢仔细分析。
对于期望状态的设计：
1.多个终点一个起点，就f[i]表示，从i到终点的期望步数，f[s]即为答案
2.多个起点一个终点，就f[i]表示，从起点到i的期望步数，f[t]即为答案
3.与终点无关的树形期望dp，通常往子树对i，父亲对i影响考虑，和一般的树形dp类似。
