PKUSC2019 D2T2

PKUSC2019 D2T2

把n(n<=100)的树（无边权）放在m维空间上（坐标都是整点），使得任意两个点的曼哈顿距离都是原树上的距离

求最小的m，并给出构造方案

 

性质好题，巧妙构造题。

原树上相邻的边，一定是某一维+1或者-1，其他不变

先确定一个根，不妨给每个边一个+i或者-i，表示这个边指向的儿子从父亲过来，增加了第i个基向量或者减去

以+(1,0,0,0...),-(1,0,0,0...)为例（简称+1，-1）

 

发现，两个点(x,y)曼哈顿距离可能比树上的实际距离小，这一定是因为，(x,y)路径上的某一次向量改变相互消去了！

 

结论一：

+1或者-1一定是直上直下的链（可以不连续），否则出现

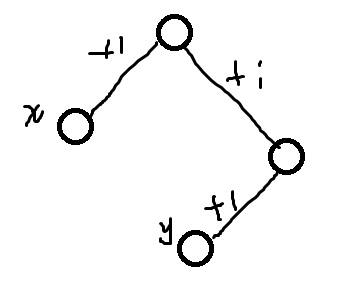
那么(x,y)的距离，实际上两个+1减法减掉了。

结论二：

+1和-1不能存在祖先后代关系

否则出现：

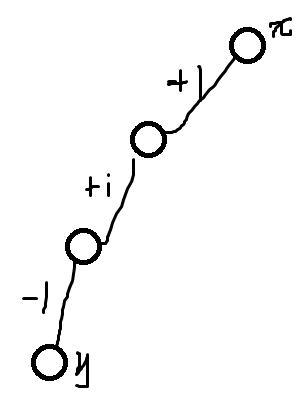
那么（x，y）的距离还是把+1和-1做和消掉了。

 

 

但是，为了保证m最小，每一维的应当充分利用。

所以+1，-1连续的链一定不劣。

如果叶子个数为k，m最小值为k/2上取整。

每个叶子头上是+1,-1,+i,-i,+j,-j。。。。

 

构造可以达到最小值：

如果暴力把基向量往上填的话，会出现这样的情况：

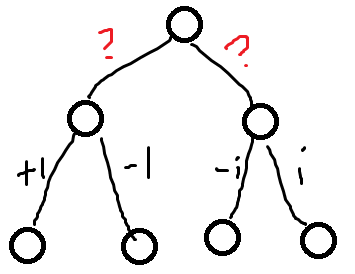
问号只能填新的维度，这样就浪费了。

最优情况显然是：

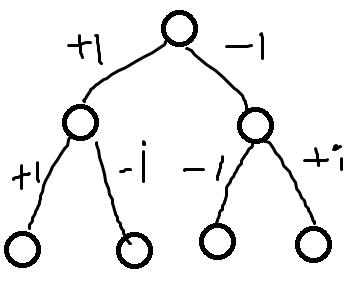
所以，相同维度的叶子，往上爬，要么不相遇（被之前维度隔断），要么只能在根节点相遇。

令重心（这里重心定义为，任何一个子树的叶子个数<=k/2）为根，i叶子和i+k/2叶子配对。

这样，相同维度的叶子，一定来自根的不同子树，一定合法！