[题集]图论
生成树
MST?Kruskal过程:贪心、重构树
prufer序列:一般树,森林,有根树,用于DP或者打暴力
Matrix-Tree定理:给定图求生成树个数,邻接矩阵数字表示边权
多次求MST或者多次加边等等:考虑缩点
一些图的问题:找到生成树处理(如Tarjan的dfs树,支配树,最短路树)
1.[Ctsc2014]图的分割
考虑Kruskal的过程,发现恰好可以直接贪心!
2.51Nod1446 限制价值树
两部分,折半枚举合法集合,统计生成树个数
3.
最小生成树计数:排序kruskal时候,缩点配合矩阵树
4.[APIO2013]道路费用
还是枚举哪些边会最终贡献,为了提高效率,进行缩点
5.[HNOI2010]城市建设
cdq分治,把一定不会在最小生成树的边提前删掉,一定在的提前加上。其实还是缩点提高效率
最短路
常用dij和floyd(spfa)
考虑某些边、点和最短路关系,往往需要统计每个点开始、结束的最短路信息
还有一些建超级汇的操作
最短路树,最短路DAG,或者任意某条最短路都可以做文章
两个源汇的确切路径,考虑分层分步
例题1
你在一个国家旅游,国家可以看做有向图
• 每一条边都有过路费
• 在每一个点,你可以选择花费 𝑝𝑖 购买魔法棒,当你持有魔法棒时,
你所经过的所有边都会永久免费(第一次也不需要付钱),但是
最后你必须把魔法棒放回这个点
• 你可以无限购买魔法棒
每个SCC至少购买一个魔法棒
• 求能经过尽量多的城市的前提下,你所花费的最小代价
求SCC,topoDp
对于每个SCC,要知道从某个点开始,走若干个边,然后买魔法棒的最小花费
买魔法棒就停止了,可以当做终止节点
多起点多终点?
每个终点向T连接pi的边,然后从T跑最短路即可
例题2
• 给出一张图,每个点上有很多人,每条边上也有很多重边
• 设一个点的重要程度为
Pr表示概率
• 求每个 v𝑝
• 𝑛 ≤ 3000, 𝑚 ≤ 10000 Vp = §,
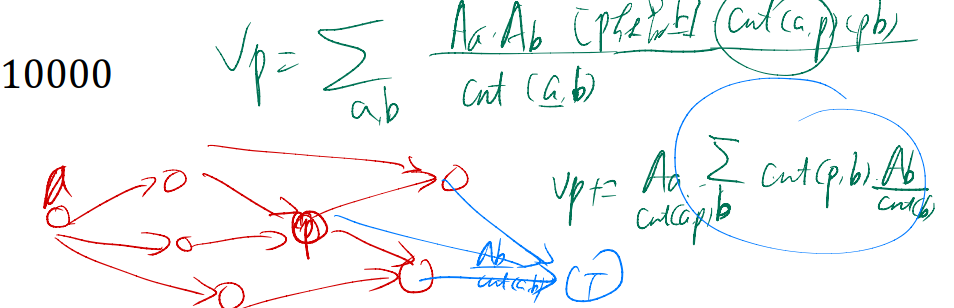
cnt(a,b)表示a到b的最短路径条数
直接的式子是枚举p再枚举a,b,O(n^3)
考虑能不能“继承点东西”降低复杂度
具体地,枚举A,给所有的p贡献可能的B
对于A,求出A的最短路径DAG
对于一个p,p能到达的节点B,AB的最短路,p都是可行点

但是cnt(p,b)不能分离,看起来还是3次方的
发现,p后面的DAG,恰好一定也是p的最短路径DAG的一部分!
所以倒序topo,每个点T有一个权值T/cnt(A,T),后继贡献直接加起来,cnt(p,b)自然就得到了
例题3:
• 给出一张 DAG,求出有多少点对 𝑎, 𝑏,使得任意从 𝑠 到 𝑡 的路径
都恰好经过 𝑎, 𝑏 中的任意一点
• 𝑛, 𝑚 ≤ 100000
考虑两个点a,b合法的充分必要条件:
1.a,b互不可达
2.cnt[s][a]*cnt[a][t]+cnt[s][b]*cnt[b][t]=cnt[s][t]
topo搞到拓扑序和cnt,
把val[*]=cnt[s][*]*cnt[*][t]进行离散化,开值域个bitset
倒序考虑拓扑序,枚举a
bitset处理可以到达的集合S
得到val[b]的值,S取反,和这个val[b]的bitset取交,交的个数就是贡献
然后把val[a]的a位置设置为1
这样就保证了a,b互不可达
例题4
给出一棵树,边权为正
随机选出 𝑘 个关键点,然后选择一种移动总距离最短的方案,从
其中某个点出发,经过每个关键点至少一次
求出移动总距离最短的方案的期望
𝑛 ≤ 500
总距离最短:虚树总边长*2-直径
虚树总边长*2:考虑边的贡献,两边一共选择k个
直径:支持单点增量
不妨直接枚举直径(a,b),考虑对应的点集个数
如果(a,b)加入p之后合法,也即max(dis(p,a),dis(p,b))<dis(a,b),那么p可以加入
这样从所有能加入的p中选择k-2个即可得到所有的方案数
但是一个虚树多个直径可能算重
方法:
每个边(u,v)不妨u<v ,有额外权值:2^(-u),
这样,一个虚树直径一定会在字典序最小的位置被求恰好一次,就完全分开了
例题5
给出一张有向图,每条边上有数字
对每一对点对 𝑥, 𝑦 ,求从 𝑥 到 𝑦 的最短的回文路径
𝑛 ≤ 500, 𝑚 ≤ 10^5
分成两步走
f[a][b]表示a到b的最短路
每次让a走一步
g[a][b][char]表示该b走了,a上一步走的字符是char的最短路
例题6
删边最短路
差分约束
如果能从题目中找到二元一次不等关系,即可差分约束
可以求一组最值解或者判断有无解
是数形结合的思想
可能无解,所以时而还配合于二分
例题1
51nod地铁环线
可行的总长是一段区间
考虑二分总环长+SPFA判定
先找右端点,再找左端点,
问题是不合法的时候mid是大还是小
以最短路为例,x=mid
每个边权值可以看做:kx+b
如果一个负环总和为Kx+B<=0
根据K的正负即可判定x过大还是过小
K=0显然就无解了。
例题2
THUSC2018
圆环上有 𝑚 对蓝点,每一对蓝点之间连了一条强度为 𝑘𝑖 的线段
你需要在切割若干次,每次是用一条直线切割所有经过的线段
如果一条线段被切割超过 𝑘𝑖 次,它就坏了
求至少要切割几次
𝑛 ≤ 3000, 𝑚, 𝑘𝑖 ≤ 10000
每个线段两侧都至少>=k个切割点
对于所有的切割点,i和i+tot/2进行连边
每个线段也会恰好被切割k次
同上题
甚至直接二分即可,不用Kx+b
拓扑排序
DAG是具有优美性质的图
topo排序是分层图的思想
topo序的先后含有一些到达关系
例题1
给出一张无向图
求一个最大的子图,使得每个点的度数都不小于 𝑑
𝑛 ≤ 10^6
不断删除度数小于d的点即可
例题2
两个人在 DAG 上走,每个人都有自己的起点和终点
求两个人不经过一条边的方案数(这里不经过同一条边指的是:路径的边没有交集)
𝑛, 𝑚 ≤ 1000
还是分层变成回合制。使得多了一些可以共用的中间状态
f[a][b]表示达到(a,b)的方案数
每次topo序小的先走
不经过同一条边?不能连续(i,i)->(j,j)
所以,中间变量g[a][b][0/1]表示一个走到a,一个走到b,上一次是否位置相同的方案数
O(nm)
例题3
topo序好题
2-SAT
命题蕴含关系
各种优化建图
例题1
最难办的是:最多说一句谎
只给每个犯人开两个点
每个犯人处理:他说的,和说他的
1.他是犯人
说他不是犯人的都是犯人
说他是犯人的人,只说了这一句谎,所以这些人的说的其他话都是真的。暴力连边O(m^2)前缀后缀优化即可
2.他不是犯人
说他是犯人的都是犯人
他说的话都是真的
Tarjan求方案即可
网络流
过于博大精深
度数回路上下界:先走完限制,再调整
范围较小的值域限制:切糕割
且关系的收益,或关系的花费:每个关系建新点
二元或关系的收益,且关系的花费:隔断含义反转,二元关系最小割。(前提:涉及的点对构成二分图(这个“点”也可以是集合的且,详见例题4))
一些依赖的带点权最大化问题:最大权闭合子图
匹配问题的DP:网络流的匹配关系可以优化DP,否则只能状压DP
如果有些东西一定会被计算:整体+权值可以把负权变成正权
各种网格、横纵等:都具备一定二分图性质,翻转连边,匹配
还有一些特殊题型和翻转
例题1
给出一张无向图,每条边有一个次数限制
你需要找一条总长度尽量短的可以不是简单路径的回路,使得它
经过每条边至少那么多次
𝑛 ≤ 500
直接干掉下界
回路?每个点度数为2
两点之间走一条路径,只会使得起点终点度数奇偶改变
考虑奇度数节点,两个奇度数节点之间连接距离长度的边权
找一个最小权完美匹配即可
例题2
给出若干个定义在[0, 𝑚] 的分段一次函数
请你把这些一次函数分成最少若干个组,使得每个组内的一次函数两
两不相交
n<=250
不相交关系,形成DAG,求最小链覆盖即可
例题3
经典且或关系问题
例题4
有一个网格,每个格子你可以决定买不买
如果你买了一个格子,就要花费其价格
如果你买了一个格子,或者买了和这个格子相邻的所有格子,你
可以获得这个格子的收益
最大化收益减去价格
n,𝑚 ≤ 100
或有贡献,发现正是二分图!
含义反转,贡献关系单独表示成点
本质上还是两个“点”的或关系,一个满足有收益
这样建图:

黑白染色成为左右部点
ans+=所有收益
S到左部点cosi,右部点到T连cosi
由于共同收益和单点购买的收益一样,所以每个点像上图一样连好关系
这样只要左边都选,或者这个点选择,那么这个收益就可以保留,否则收益必须割掉
例题 5
例题 6
弯弯国
• 给出一张网格图,网格上有一些障碍
• 你需要给每个没有障碍的网格放一个恰好连接网格的两条边的轨
道,同时使得这个轨道的两端都和其他轨道的两端相连
• 在一些格子里生活着一些弯的人,他们希望能让自己所在的格子
里的铁轨是弯的
• 求最多能满足多少弯人的要求
• 𝑛, 𝑚 ≤ 50
有点类似「清华集训 2017」无限之环
把所有弯的贡献都加上
直有花费
弯?一个向上下,一个向左右
直?都向上下,或者都向左右
拆边费用流!
上面两个点连接上、下
下面两个点连接左、右
这样直一定有惩罚,弯不会有惩罚!
最小费用最大流!
例题7
真实·网络流优化DP
• 在树上选出两个尽量大的不相交的同构的连通块
• 𝑛 ≤ 50
同构?
枚举边
一半的根就是边的端点,枚举另一半的树根
有根树,f(i,j)i为根,j为根的最大连通块,对于du^2的儿子进行带权最大匹配
O(n^7)
发现,可以记忆化!
因为另一半树根变化,其他的边只是方向变化
f(e,j)一半边e(带方向),确定根的一半的j的子树
可以记忆化
O(n^6)
非常不完全n^6,可过
例题8
在地图上有一些敌人,每个敌人有一个消灭可获得的价值
地图上还有很多的发射器,每个发射器有最大的射程限制,同时
有一个朝向,保证没有面对面的发射器
你可以对每个发射器指定一个射击距离,这个发射器就会消灭发
射器朝向的这个方向的、距离恰好为这个射击距离的敌人,但是
要求两个发射器射击时经过的格子不能相交
求最多能消灭多少价值的敌人
𝑛, 𝑚 ≤ 50
范围很小,还有限制,考虑切糕割
但是这里的收益很难都算上然后扣去
但是由于每个发射器都要发射一定是最优的
所以每个边的流量是-v(i,j)+M,M是这一行的价值和
考虑用inf边限制不能相交,只用考虑横和纵
若x>=a,则y<b,若y>=b则x<a
如果连边都是同一个方向,一个更小反而不合法
由于横纵二分图,把横反过来连边
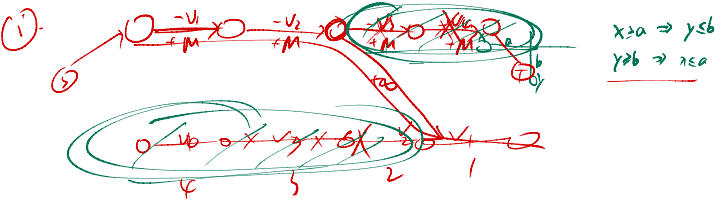
即可
例题9
给出一棵树,然后给树上每一条边染色,要求每个点的出边颜色
互不相同
• 最小化每条边所染颜色的编号和
• 𝑛 ≤ 150
设f[i][c]以i为根子树,father到i的边的颜色是c的最小编号和
颜色互不相同?匹配!
枚举f[i][c]
S-每个儿子-分别连每个颜色c+f[soni][c]的边-每个颜色连到T边权为1
最小费用最大流
O(n*m*dinic)
例题10
• 给出一张无向图
• 请你往图上加一些边
• 加完边后,设点 𝑝 的距离是dp,那么总得分是 ∑c(p,dp)
• 最大化得分
𝑛 ≤ 50
其实最后只要满足,对于原来有边相连的点对(x,y)最后必然有|disx-disy|<=1
所以切糕割即可
一定有一种方案还原
例题11
另类网络流
例题12
给出一张无向图,每条边有一个经过时间
• 现在有 𝑐 个乘客,它们分别在第 𝑝i个点,并且都想前往点 1
• 所有人都只想走一条最短路,并且同时从起点出发
• 如果两个人同时同向经过同一条边,那么堵塞了,不合法
• 请你求出一个尽量大的乘客的子集,使得不会出现拥塞
找最短路径图
最短路不同,不会堵塞
对于最短路相同的所有人,分别跑一遍最大流


