[题集]串
字典序问题
求最优化:按位贪心
第k小
按位枚举,看满足的是否存在k个
定义集合字典序为排序后的字典序
第k大子集:按位贪心(二分?看情况)
比某个集合大k:枚举LCP「LibreOJ NOI Round #1」验题
字典序比较:枚举LCP
例题1
给出 𝑛 个字符串,字符集为 10
每次输入一个 10 的排列来规定 10 种字符的字典序
询问第 𝑖 个串在这种字典序下排名第几
LCP
建trie树,两者字典序不同一定有分叉,而分叉走下去的字符是比较关键。cnt[a][b]表示到根路径上,因为字符a,b之差而分叉的个数
离线+dfs
已知小串的子串问题
套路:KMP、AC 自动机
AC 自动机和子串的位置关系、fail 指针
例题 1
• 给出一棵树
• 每次给出一个串,询问一条路径上这个串作为子串出现了多少次
• 𝑛, 𝑚 ≤ 10
经典问题
离线,差分,阿狸的打字机
跨域LCA部分暴力
例题2
你需要维护一棵 Trie
每次插入一个叶子节点,然后你要输出这个叶子节点到根的这条
路径的最长的“前缀 = 后缀”的长度
𝑛, 𝑚 ≤ 1000000
就是KMP了。
不能暴力跳,利用fail指针加速
但是必须是在这个到根链上的出边
所以建主席树
每个点对于每个分叉出去的边都建一个往这方向走的到根路径上的出边集合(和fail的出边合并)
每个点再维护一个初始的到根路径上的主席树
新加入一个点x,通过fa找到fail,x初始主席树就是fail的这个方向出边的主席树
然后fa对于这个方向,新建一个主席树,这个出边节点指向x
例题3
• 你有两个串集合 S 和 T,S 是固定的,T 会在操作中修改
• 每次操作:T 集合加一个串、询问 T 里面有多少个串包含 S[i]
bzoj3881: [Coci2015]Divljak
S建AC自动机
加入一个T,途经的点直接fail树上所有的点都会增加一次出现,
为了不重复,就是链并上的点+1
LCT维护fail树,直接tag标记表示每个点最近一次颜色是哪一个
access时候判断是否已经是当前颜色即可。
O(nlogn)
已知大串的子序列问题
• 一般模式:给出一个大串,求其子序列的一种信息
• 包括最优化和计数两类问题
• 其中计数问题包括两种:位置不同算多种/内容不同算多种
• 包括一系列公共子序列问题
• 对于位置不同的问题(或者最优化问题),只需要记录 𝑓 𝑖 这样
的状态即可,表示所有右端点不超过 𝑖 的子序列的信息
• 对于内容不同的问题,我们需要另一些思想
记录每个位置每个字符下一次第一个出现的位置
可建DAG,也即序列自动机
可以直接进行匹配和统计
内容不同子序列计数问题
例题1
求一个字符串有多少内容不同的回文子序列
𝑛 = 5000, Σ = 10
f[l][r]表示,以l,r结尾的答案
f[l][r]=∑f[nxt[w]][las[w]]+(l<=r)+(l<r)
也就是往里面选择一些+自己
记忆化搜索
首尾加上相同特殊字符,即可直接调用f[0][n+1]得到答案
例题2
• 给出两个串,求他们所有内容不同的公共上升子序列个数
• 𝑛 = 5000, Σ = 𝑛
不会
已知大串的子串问题
• 对于已知大串的题,一般是考虑维护一个结构,来表示这个大串
内的所有子串,同时还能体现出这些子串的(前后缀)关系
• 一般的方法分为两种:后缀树(数组)、SAM
• 前者转化为边长和的统计,后者转化为路径的统计
(PS:先考虑SAM和后缀树,毕竟是树形结构方便。SA其次考虑(HEOI2019 D1T2就这样没有想出来。。。))
例题 1
• 给出一棵树,点上有字符
• 求所有的直上直下的路径构成的不同串有多少种
• 𝑛 ≤ 10^6,字符集较大
字符集大,不能用广义SAM
剩下后缀数组
直接每个点到跟的路径看做后缀
后缀排序。倍增,和树上倍增恰好契合,直接利用2^(k-1)的排序结果即可。
求height用hash+二分,
ans=∑dep-∑hei
例题2
• 给出一个串
• 每次给出 𝑙, 𝑟, 𝑘,在 𝑙, 𝑟 中找一个 𝑖 使得 LCP(𝑠(k,n), 𝑠(i,n) ) 最大
• 𝑛, 𝑚 ≤ 10^6
k的后缀的排名在[l,r]的前驱后继找到即可
后缀数组+主席树(前缀后缀)
后缀数组+离线线段树
例题3
二分LCP长度mid,看rk[c]最多延伸的区间[le,ri],看这个区间里面是否有sa为[a,b-mid+1]的
主席树差分判断是否出现
注意:
1.lcp时候,++p1
2.rk,sa别写反

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Miracle{ const int N=1e5+5; int n,m; char s[N]; int hei[N],sa[N],rk[N]; int xx[N],yy[N],buc[N]; int f[N][18],lg[N]; void SA(){ int m=130; int *x=xx,*y=yy; for(reg i=1;i<=n;++i) ++buc[x[i]=s[i]]; for(reg i=1;i<=m;++i) buc[i]+=buc[i-1]; for(reg i=1;i<=n;++i) sa[buc[x[i]]--]=i; for(reg k=1;k<=n;k<<=1){ int num=0; for(reg i=n-k+1;i<=n;++i) y[++num]=i; for(reg j=1;j<=n;++j){ if(sa[j]-k>0) y[++num]=sa[j]-k; } for(reg i=1;i<=m;++i) buc[i]=0; for(reg i=1;i<=n;++i) ++buc[x[i]]; for(reg i=2;i<=m;++i) buc[i]+=buc[i-1]; for(reg i=n;i>=1;--i) sa[buc[x[y[i]]]--]=y[i],y[i]=0; swap(x,y); num=1;x[sa[1]]=1; for(reg i=2;i<=n;++i){ x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&(y[sa[i]+k]==y[sa[i-1]+k]))?num:++num; } if(num==n) break; m=num; } } void HEI(){ for(reg i=1;i<=n;++i) rk[sa[i]]=i; int k=0; for(reg i=1;i<=n;++i){ if(k) --k; if(rk[i]==1) continue; int j=sa[rk[i]-1]; while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k]) ++k; hei[rk[i]]=k; } for(reg i=1;i<=n;++i) { lg[i]=(i>>(lg[i-1]+1))?lg[i-1]+1:lg[i-1]; f[i][0]=hei[i]; } for(reg j=1;j<=17;++j){ for(reg i=1;i+(1<<j)-1<=n;++i){ f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]); } } //;//build rmq } int lcp(int p1,int p2){ // cout<<" lcp "<<p1<<" "<<p2<<" "<<n-rk[p1]+1<<endl; if(p1==p2) return n-sa[p1]+1; // p1=sa[p1],p2=sa[p2]; if(p1>p2) swap(p1,p2); ++p1; int len=lg[p2-p1+1]; return min(f[p1][len],f[p2-(1<<len)+1][len]); } struct node{ int ls,rs; int sum; }t[40*N]; int tot; int rt[N]; void pushup(int x){ t[x].sum=t[t[x].ls].sum+t[t[x].rs].sum; } void upda(int &x,int y,int l,int r,int p){ x=++tot; t[x]=t[y]; if(l==r){ ++t[x].sum;return; } int mid=(l+r)>>1; if(p<=mid) upda(t[x].ls,t[y].ls,l,mid,p); else upda(t[x].rs,t[y].rs,mid+1,r,p); pushup(x); } int query(int x,int y,int l,int r,int L,int R){ if(L<=l&&r<=R){ return t[x].sum-t[y].sum; } int mid=(l+r)>>1; int ret=0; if(L<=mid) ret+=query(t[x].ls,t[y].ls,l,mid,L,R); if(mid<R) ret+=query(t[x].rs,t[y].rs,mid+1,r,L,R); return ret; } bool che(int a,int b,int pos,int len){ b=b-len+1; if(a>b) return false; if(!len) return true; pos=rk[pos]; // cout<<" che "<<a<<" "<<b<<" pos "<<pos<<" md "<<len<<endl; int le=pos; int L=1,R=pos; while(L<=R){ int mid=(L+R)>>1; int now=lcp(mid,pos); if(now>=len) le=mid,R=mid-1; else L=mid+1; } L=pos,R=n; int ri=pos; while(L<=R){ int mid=(L+R)>>1; int now=lcp(pos,mid); // cout<<mid<<" now "<<now<<endl; if(now>=len) ri=mid,L=mid+1; else R=mid-1; } // cout<<" le "<<le<<" ri "<<ri<<endl; int lp=query(rt[ri],rt[le-1],1,n,a,b); if(lp>0) return true; return false; } int main(){ rd(n);rd(m); scanf("%s",s+1); SA();HEI(); // prt(sa,1,n); // prt(rk,1,n); // prt(hei,1,n); for(reg i=1;i<=n;++i){ upda(rt[i],rt[i-1],1,n,sa[i]); } int a,b,c,d; while(m--){ rd(a);rd(b);rd(c);rd(d); int L=0,R=d-c+1; int ans=0; while(L<=R){ int mid=(L+R)>>1; if(che(a,b,c,mid)) ans=mid,L=mid+1; else R=mid-1; } printf("%d\n",ans); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
字符串综合练习
树上后缀排序
倍增即可。常数优化?
看i207M的吧
巧妙运用三关键字排序,并且注意可重复、不可重复的搭配。
fa也不用倍增,直接循环找一遍即可。
还有我的辣鸡代码:(直接无视编号排好序,再sort+dfs)

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Miracle{ const int N=5e5+5; int n; vector<int>to[N]; char s[N]; int dep[N]; int fa[N][20]; int lim; void dfs1(int x){ lim=max(lim,dep[x]); for(solid y:to[x]){ dep[y]=dep[x]+1;dfs1(y); } } int mem[N],num; int sa[N],rk[N]; int xx[2*N],yy[2*N],buc[N],pos[N]; void SA(){ int m=130; int *x=xx,*y=yy; for(reg i=1;i<=n;++i) ++buc[x[i]=s[i]]; for(reg i=1;i<=m;++i) buc[i]+=buc[i-1]; for(reg i=1;i<=n;++i) sa[buc[x[i]]--]=i; for(reg k=0;k<20;++k){ if((1<<k)>lim) break; // cout<<" kk "<<k<<endl; int num=0; for(reg i=1;i<=n;++i){ if(fa[i][k]==0) y[++num]=i; } for(reg i=1;i<=m;++i) buc[i]=0; for(reg i=1;i<=n;++i){ if(fa[i][k]){ ++buc[x[fa[i][k]]]; } } for(reg i=1;i<=m;++i) { buc[i]+=buc[i-1]; pos[i]=num+buc[i]; } for(reg i=1;i<=n;++i){ if(fa[i][k]){ y[pos[x[fa[i][k]]]--]=i; } } for(reg i=1;i<=m;++i) buc[i]=0; for(reg i=1;i<=n;++i) ++buc[x[i]]; for(reg i=1;i<=m;++i) buc[i]+=buc[i-1]; for(reg i=n;i>=1;--i){ sa[buc[x[y[i]]]--]=y[i];y[i]=0; } swap(x,y);num=1; x[sa[1]]=1; for(reg i=2;i<=n;++i){ x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[fa[sa[i]][k]]==y[fa[sa[i-1]][k]])?num:++num; } if(num==n) break; m=num; } } bool cmp(int a,int b){ return xx[a]==xx[b]?a<b:xx[a]<xx[b]; } void dfs2(int x){ mem[++num]=x; for(solid y:to[x]){ dfs2(y); } } int main(){ rd(n); dep[1]=1; for(reg i=2;i<=n;++i){ rd(fa[i][0]);to[fa[i][0]].push_back(i); } for(reg j=1;j<=19;++j){ for(reg i=1;i<=n;++i){ fa[i][j]=fa[fa[i][j-1]][j-1]; } } dfs1(1); scanf("%s",s+1); SA(); // prt(xx,1,n); memset(buc,0,sizeof buc); num=0; for(reg i=1;i<=n;++i){ sort(to[i].begin(),to[i].end(),cmp); } dfs2(1); // prt(mem,1,num); for(reg i=1;i<=n;++i) ++buc[xx[i]]; for(reg i=1;i<=n;++i) buc[i]+=buc[i-1]; for(reg i=n;i>=1;--i){ xx[mem[i]]=buc[xx[mem[i]]]--; sa[xx[mem[i]]]=mem[i]; } // prt(xx,1,n); prt(sa,1,n); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
区间回文子串
给出一个串
每次询问一个区间中有多少子区间是回文的
𝑛, 𝑚 ≤ 10^6
manacher求出回文半径p[],
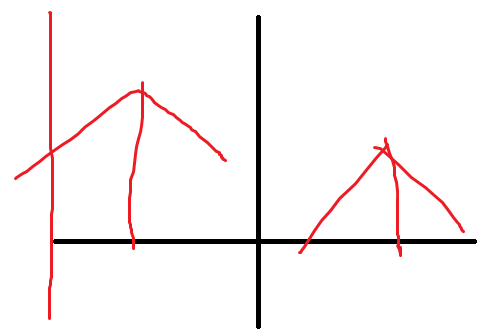
根据在mid的左右分别考虑,左右分别和l,r卡边界
开主席树维护i-p[i],i+p[i]即可。
判断AC自动机相等
给出两个串的集合 A、B
判断“所有包含 A 中一个串作为子串的串的集合”和“所有包含 B中
一个串作为子串的串的集合”是否相等
长度 ≤ 2000
即,是否存在一个串使得存在A的子串不存在B的或者存在B的不存在A的
直接从(x,y)表示A匹配到了x,B匹配到了y,都没有出现过A,B作为子串
大力BFS
枚举出边1~26,如果到达一个能出现,一个不能出现的状态那么就不等了
能同时到达能出现的状态,不管。
还是都不能出现,加入queue
THUSC2018
• (THUSC2018 D1T2)
• 给出 𝑛 和 𝑚 个和谐串,求有多少长度为 2𝑛 的形如 𝐴𝐴 的串,不
包含 𝑘 个和谐串不相交地出现
• 𝑛 ≤ 100, 𝑚 ≤ 200, s ≤ 5, 𝑘 ≤ 5
形如AA?
并不是枚举分界点!
外层枚举第二个A开始匹配的位置M
f[i][j][k]第一个A匹配到了i,第二个匹配到了j,划分了k个
能划分就直接划分,回到起点
开始f[0][M][0] 最后就是f[M][*][<k]
后半段M开始也是直接能划分就划分
不可能最后得到的字符串划分有相交

因为这样,到了绿色位置就直接回起点了,不可能再到M了。
概率题
给出串集合 𝑆
我们随机生成串,每次以 pi 的概率生成第 𝑖 个字母
一旦生成的串包含 𝑆 里面所有串作为子串,就停止
求期望生成多长
𝑆 ≤ 8, 𝑠 ∈ 𝑆 ≤ 6
状压。成环。高斯消元。对S相同的进行高斯消元,2^8*(50^3)
多串本质不同子串

倒着做,
把si没有出边的指到下一个自动机的初始节点
DP统计路径
每个本质不同的串会在出现字典序最小的位置被统计一次
最长反链
给出一些字符串
你要从中选择一个集合,使得任意一个串不是另一个串的子串
求集合的最大大小
𝑛 ≤ 2000, ∑𝑠<= 10^7
fail树的祖先和自己不能在一起
最长反链=最小链覆盖
求最小链覆盖即可。
51nod 1600 Simple KMP
• 给出一个字符串
• 对字符串的每个前缀,输出这个前缀的 KMP 的 fail 树的深度之和
• 𝑛 ≤ 10^5
不断跳kmp,感觉像是统计贡献
可以发现,就是以i为结尾的子串在[1,i-1]的出现次数,树剖维护right集合大小即可
THUWC2018
给出一个大串 𝑆
每次给出一个小串 𝑡,询问把 𝑡 插在 𝑆 中的哪一个位置能使插完
之后的字符串的字典序最小
多个位置输出编号最小的位置
𝑆, ∑𝑡 ≤ 10^6
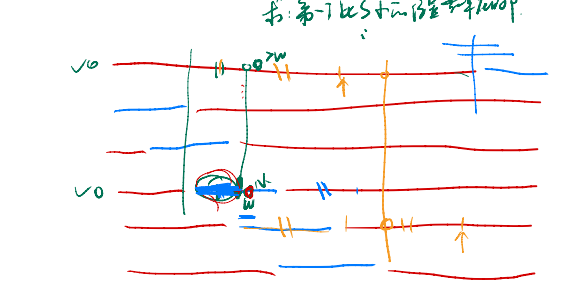
考虑为什么要插入t,一定要使得比s的字典序要大,否则不如插到最后面
所以考虑和原串的字典序关系。
枚举lcp=0~|t|,看下一个!
也就是t在s上匹配
匹配到了t的前缀i
SAM上找存在下一个字符<t[i+1]的最靠前的起始位置j,把j插入一个数组里
一旦失配就break
全部匹配?。。。。还是考虑下一个比t[1]字典序小的最靠前的位置
s最前面尝试插入t
s最后2*|t|位置尝试插入t
这些尝试都加入数组
哈希+二分判断
这样我们每个插入位置i以插入后与s[1..i]+t的lcp为标准进行考虑了。


