[BJOI2019]勘破神机
推式子好题
m=2,斐波那契数列,$f_{n+1}$项
不妨$++l,++r$,直接求$f_n$
求$\sum C(f_n,k)$,下降幂转化成阶乘幂,这样都是多项式了,方便交换求和号
最后面的斐波那契数列用通项公式求。二项式展开。
交换求和号之后,枚举i,j 最后一项是等比数列求和。
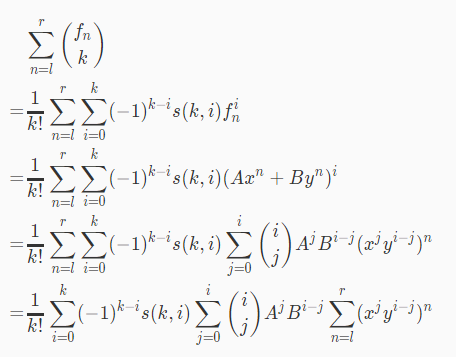
m=3,
n为奇数是0
n是偶数时,令n=n/2 递推公式:$g_n=4\times g_{n-1}+g_{n-2}$
证明:枚举从后往前第一个完全分出的块,除了块长为2的方案额外多一个外,其它都是两种。$g_n=g_{n-1}+2\times \sum_{i=0}^{n-1} g_{i}$
再写出:$g_{n-1}=g_{n-2}+2\times \sum_{i=0}^{n-2} g_{i}$两式做差移项即可得到。
用特征方程可以解得$g_n$的通项公式
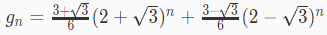
$\sqrt 5$在mod 998244353下不存在,可以用$a+b\sqrt5$形式表示
注意,等比数列求和:$1+Q+....+Q^n=\frac{1-Q^{n+1}}{1-Q}$注意是n+1,因为有n+1项
#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Miracle{ const int mod=998244353; const int N=505; int C; int ad(int x,int y){ return x+y>=mod?x+y-mod:x+y; } int mul(int x,int y){ return (ll)x*y%mod; } ll qm(ll x,ll y){ ll ret=1; while(y){ if(y&1) ret=mul(ret,x); x=mul(x,x); y>>=1; } return ret; } int inv[1000000+5]; int ni(int x){ // cout<<" ni x "<<x<<endl; return x<=1000000?inv[x]:qm(x,mod-2); } struct po{ int a,b; po(){ a=0;b=0; } po(int aa,int bb){ a=aa;b=bb; } po friend operator +(po a,po b){ return po(ad(a.a,b.a),ad(a.b,b.b)); } po friend operator -(po a,po b){ return po(ad(a.a,mod-b.a),ad(a.b,mod-b.b)); } po friend operator ~(po a){ int mom=ni(ad(mul(a.a,a.a),mod-mul(C,mul(a.b,a.b)))); // cout<<" mom "<<mom<<endl; return po(mul(a.a,mom),ad(0,mod-mul(a.b,mom))); } po friend operator -(po a){ return po(ad(0,mod-a.a),ad(0,mod-a.b)); } po friend operator *(po a,po b){ return po(ad(mul(a.a,b.a),mul(mul(a.b,b.b),C)),ad(mul(a.a,b.b),mul(a.b,b.a))); } po friend operator *(po a,int c){ return po(mul(a.a,c),mul(a.b,c)); } po friend operator /(po a,po b){ return a*(~b); } void op(){ cout<<" a "<<a<<" b "<<b<<endl; } }A,B,X,Y,mi[N][4]; po qm(po x,ll y){ po ret;ret.a=1; while(y){ if(y&1) ret=ret*x; x=x*x; y>>=1; } return ret; } po calc(po Q,ll n){ // Q.op(); if(Q.a==1&&Q.b==0){ return po((n+1)%mod,0); } po tmp=Q;tmp=qm(tmp,n+1); tmp=-tmp;tmp.a=ad(tmp.a,1); Q=-Q;Q.a=ad(Q.a,1); // Q.op(); // Q=~Q; // Q.op(); return tmp*(~Q); } int s[N][N],c[N][N]; int main(){ int t;rd(t);int m;rd(m); inv[1]=1; for(reg i=2;i<=1000000;++i){ inv[i]=mul(mod-mod/i,inv[mod%i]); } if(m==2) { C=5;A=po(0,ni(5));B=po(0,mod-ni(5)); X=po(ni(2),ni(2));Y=po(ni(2),mod-ni(2)); } else { C=3;A=po(ni(2),ni(6));B=po(ni(2),mod-ni(6)); X=po(2,1);Y=po(2,mod-1); } mi[0][0]=mi[0][1]=mi[0][2]=mi[0][3]=po(1,0); for(reg i=1;i<=502;++i){ mi[i][0]=mi[i-1][0]*A; mi[i][1]=mi[i-1][1]*B; mi[i][2]=mi[i-1][2]*X; mi[i][3]=mi[i-1][3]*Y; } s[0][0]=1; for(reg i=1;i<=502;++i){ for(reg j=1;j<=502;++j){ s[i][j]=ad(mul(s[i-1][j],i-1),s[i-1][j-1]); } } c[0][0]=1; for(reg i=1;i<=502;++i){ c[i][0]=1; for(reg j=1;j<=502;++j){ c[i][j]=ad(c[i-1][j-1],c[i-1][j]); } } ll l,r,k; while(t--){ rd(l);rd(r);rd(k); if(m==2) { ++l,++r; po ans; for(reg i=0;i<=k;++i){ // cout<<" i "<<i<<endl; po tmp; for(reg j=0;j<=i;++j){ // cout<<" jj "<<j<<endl; tmp=tmp+mi[j][0]*mi[i-j][1]*(calc(mi[j][2]*mi[i-j][3],r)-calc(mi[j][2]*mi[i-j][3],l-1))*c[i][j]; // cout<<" bac "<<endl; } if((k-i)&1) tmp=-tmp; ans=ans+(tmp*s[k][i]); } for(reg i=1;i<=k;++i) ans=ans*inv[i]; ans=ans*qm((r-l+1)%mod,mod-2); printf("%d\n",ans.a); } else{ ll L=l,R=r; l=(l+1)/2,r=r/2; po ans; for(reg i=0;i<=k;++i){ // cout<<" i "<<i<<endl; po tmp; for(reg j=0;j<=i;++j){ // cout<<" jj "<<j<<endl; tmp=tmp+mi[j][0]*mi[i-j][1]*(calc(mi[j][2]*mi[i-j][3],r)-calc(mi[j][2]*mi[i-j][3],l-1))*c[i][j]; // cout<<" bac "<<endl; } if((k-i)&1) tmp=-tmp; ans=ans+(tmp*s[k][i]); } for(reg i=1;i<=k;++i) ans=ans*inv[i]; ans=ans*qm((R-L+1)%mod,mod-2); // ans.op(); printf("%d\n",ans.a); } } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */

