P4233 射命丸文的笔记

P4233 射命丸文的笔记

官方题解

题意

如果一个竞赛图含有哈密顿回路，则称这张竞赛图为值得记录的

从所有含有n个顶点（顶点互不相同）的，值得记录的竞赛图中等概率随机选取一个

求选取的竞赛图中哈密顿回路数量的期望值

由于答案可能过大/丢失精度，只需要输出答案除以998244353的余数

题解

总回路数量/有回路的竞赛图数量

总回路数量：统计贡献

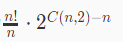
有回路的数量：

即强连通！

枚举缩点之后最小的强连通分量（这样和别的连通分量的边的方向是固定的！）

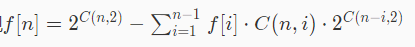
多项式求逆

 

注意：

1.求Inv时候，f[0]=1其实

2.乘法，长度是2*lp

3.C(n,2)爆int ，快速幂时候注意

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}

namespace Miracle{
const int N=1e5+5;
const int mod=998244353;
const int G=3;
const int GI=332748118;
int n;
int f[4*N],g[4*N];
int rev[4*N];
int jie[N],inv[N];
int ad(int x,int y){
    return x+y>=mod?x+y-mod:x+y;
}
int qm(int x,ll y){
    int ret=1;
    while(y){
        if(y&1) ret=(ll)ret*x%mod;
        x=(ll)x*x%mod;
        y>>=1;
    }
    return ret;
}
void NTT(int *f,int n,int c){
    for(reg i=0;i<n;++i){
        if(i<rev[i]) swap(f[i],f[rev[i]]);
    }
    for(reg p=2;p<=n;p<<=1){
        int gen;
        int len=p/2;
        if(c==1) gen=qm(G,(mod-1)/p);
        else gen=qm(GI,(mod-1)/p);
        for(reg l=0;l<n;l+=p){
            int buf=1;
            for(reg k=l;k<l+len;++k){
                int tmp=(ll)f[k+len]*buf%mod;
                f[k+len]=(f[k]-tmp+mod)%mod;
                f[k]=(f[k]+tmp)%mod;
                buf=(ll)buf*gen%mod;
            }
        }
    }
    if(c==-1){
        int iv=qm(n,mod-2);
        for(reg i=0;i<n;++i) f[i]=(ll)f[i]*iv%mod;
    }
}
int p[4*N],ni[4*N];
void Inv(int *f,int *g,int n){
    if(n==1){
        g[0]=1;return;
    }
    Inv(f,g,n>>1);
    for(reg i=1;i<n;++i) p[i]=f[i];
    p[0]=1;
    for(reg i=n;i<2*n;++i) p[i]=0;
    for(reg i=0;i<2*n;++i){
        rev[i]=rev[i>>1]>>1|((i&1)?n:0);
    }
    NTT(p,2*n,1);NTT(g,2*n,1);
    for(reg i=0;i<2*n;++i){
        g[i]=(ll)((ll)2-(ll)g[i]*p[i]%mod+mod)%mod*g[i]%mod;
    }
    NTT(g,2*n,-1);
    for(reg i=n;i<2*n;++i) g[i]=0;
}
int main(){
    rd(n);
    jie[0]=1;
    for(reg i=1;i<=n;++i) jie[i]=(ll)jie[i-1]*i%mod;
    inv[n]=qm(jie[n],mod-2);
    for(reg i=n-1;i>=0;--i) inv[i]=(ll)inv[i+1]*(i+1)%mod;
    for(reg i=1;i<=n;++i){
        g[i]=(ll)qm(2,(ll)i*(i-1)/2)*inv[i]%mod;
    }
    int lp=1;
    for(lp=1;lp<n+1;lp<<=1);
    
    Inv(g,ni,lp);
    
    lp<<=1;
    // prt(g,0,lp-1);
    // prt(ni,0,lp-1);
    for(reg i=0;i<lp;++i){
        rev[i]=(rev[i>>1]>>1)|((i&1)?lp>>1:0);
    }
    NTT(g,lp,1);
    NTT(ni,lp,1);
    for(reg i=0;i<lp;++i){
        f[i]=(ll)g[i]*ni[i]%mod;
    }
    NTT(f,lp,-1);
    // prt(f,0,lp-1);


    for(reg i=1;i<=n;++i){
        f[i]=(ll)f[i]*jie[i]%mod;
        // cout<<" i "<<f[i]<<endl;
        if(i==1) puts("1");
        else if(i==2) puts("-1");
        else{
            int tot=(ll)jie[i-1]*qm(2,(ll)i*(i-1)/2-i)%mod;
            printf("%d\n",(ll)tot*qm(f[i],mod-2)%mod);
        }
    }
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2019/4/13 19:58:12
*/