[学习笔记]树上莫队
远古博客:莫队算法——暴力出奇迹
https://blog.csdn.net/u012061345/article/details/54093879
树上莫队也就一句话:
把树上路径用欧拉序(入栈出栈序)变成区间,区间莫队即可
思想就是利用遍历构造出路径,入栈出栈相互抵消处理多余的点。
多了细节和讨论:
1.某个点存在一次贡献为1,存在两次贡献为0,
2.莫队的l,r要通过是否为祖先关系进行讨论
①是祖先关系,栈序是包含的,[in[x],in[y]]
②不是,先出栈的到后入栈的,[out[x],in[y]],LCA因为完全包含x,y所以额外再统计上
3.欧拉序是2*n个点,分块时候循环到2*n以及数组大小2*N
模板:
SP10707 COT2 - Count on a tree II

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
char ch;x=0;bool fl=false;
while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
for(x=numb;isdigit(ch=getchar());x=x*10+numb);
(fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Miracle{
const int N=40004;
const int M=100000+5;
int n,m;
struct node{
int nxt,to;
}e[2*N];
int hd[N],cnt;
void add(int x,int y){
e[++cnt].nxt=hd[x];
e[cnt].to=y;
hd[x]=cnt;
}
int co[N],b[N];
int a[2*N],tot;
int in[N],out[N];
int fa[N][18];
int dep[N];
void dfs(int x,int d){
dep[x]=d;
in[x]=++tot;a[tot]=x;
for(reg i=hd[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==fa[x][0]) continue;
fa[y][0]=x;
dfs(y,d+1);
}
out[x]=++tot;a[tot]=x;
}
int lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(reg j=17;j>=0;--j){
if(dep[fa[x][j]]>=dep[y]) x=fa[x][j];
}
if(x==y)return x;
for(reg j=17;j>=0;--j){
if(fa[x][j]!=fa[y][j]) x=fa[x][j],y=fa[y][j];
}
return fa[x][0];
}
int blo,be[2*N];
struct que{
int l,r,typ;//typ==0 need lca
int lca;
int id;
bool friend operator <(que a,que b){
if(be[a.l]!=be[b.l]) return be[a.l]<be[b.l];
if(be[a.l]&1) return a.r<b.r;
return a.r>b.r;
}
}q[M];
int ans[M];
int l,r;
int buc[N],now;
int vis[N];
void chan(int x,int c){
if(!x) return;
if(c==-1){
if(vis[a[x]]&1) c=-1;
else c=1;
--vis[a[x]];
}else{
if(vis[a[x]]&1) c=-1;
else c=1;
++vis[a[x]];
}
if(c==1){
++buc[co[a[x]]];
if(buc[co[a[x]]]==1) ++now;
}else{
--buc[co[a[x]]];
if(buc[co[a[x]]]==0) --now;
}
}
int lp;
void wrk(){
l=0;r=0;
for(reg i=1;i<=m;++i){
// cout<<"num i "<<i<<" : "<<q[i].l<<" "<<q[i].r<<endl;
while(r<q[i].r) chan(++r,1);
while(l>q[i].l) chan(--l,1);
while(r>q[i].r) chan(r--,-1);
while(l<q[i].l) chan(l++,-1);
// prt(buc,1,lp);
if(q[i].typ==1){
ans[q[i].id]=now;
}else{
// cout<<"lca "<<q[i].lca<<endl;
if(buc[co[q[i].lca]]==0) ans[q[i].id]=now+1;
else ans[q[i].id]=now;
}
}
}
int main(){
rd(n);rd(m);
blo=sqrt(n);
for(reg i=1;i<=n;++i) {
rd(co[i]);
b[i]=co[i];
}
// prt(be,1,n);
sort(b+1,b+n+1);
lp=unique(b+1,b+n+1)-b-1;
for(reg i=1;i<=n;++i){
co[i]=lower_bound(b+1,b+lp+1,co[i])-b;
}
int x,y;
for(reg i=1;i<n;++i){
rd(x);rd(y);add(x,y);add(y,x);
}
dfs(1,1);
for(reg i=1;i<=tot;++i){
be[i]=(i-1)/blo+1;
}
// cout<<tot<<endl;
// prt(be,1,tot);
for(reg j=1;j<=17;++j){
for(reg i=1;i<=n;++i){
fa[i][j]=fa[fa[i][j-1]][j-1];
}
}
for(reg i=1;i<=m;++i){
rd(x);rd(y);
int anc=lca(x,y);
// cout<<" anc "<<anc<<endl;
if(anc==x||anc==y){
if(in[x]>in[y]) swap(x,y);
q[i].l=in[x];q[i].r=in[y];
q[i].lca=anc;q[i].typ=1;
}else{
if(out[x]>in[y]) swap(x,y);
q[i].l=out[x];q[i].r=in[y];
q[i].lca=anc;q[i].typ=0;
}
q[i].id=i;
}
sort(q+1,q+m+1);
// prt(a,1,tot);
// prt(co,1,n);
wrk();
for(reg i=1;i<=m;++i){
printf("%d\n",ans[i]);
}
return 0;
}
}
signed main(){
Miracle::main();
return 0;
}
/*
Author: *Miracle*
Date: 2019/3/24 10:43:06
*/
树上带修莫队?

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define il inline
#define reg register int
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
char ch;x=0;bool fl=false;
while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
for(x=numb;isdigit(ch=getchar());x=x*10+numb);
(fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Miracle{
const int N=100000+5;
int n,m,qs;
struct node{
int nxt,to;
}e[2*N];
int hd[N],cnt;
void add(int x,int y){
e[++cnt].nxt=hd[x];
e[cnt].to=y;
hd[x]=cnt;
}
int fa[N][19];
int dep[N];
int a[2*N],tot;
int in[N],out[N];
ll w[N],v[N];
int c[N],tmp[N];
void dfs(int x,int d){
dep[x]=d;
a[++tot]=x;in[x]=tot;
for(reg i=hd[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==fa[x][0]) continue;
fa[y][0]=x;
dfs(y,d+1);
}
a[++tot]=x;out[x]=tot;
}
int lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(reg j=17;j>=0;--j){
if(dep[fa[x][j]]>=dep[y]) x=fa[x][j];
}
if(x==y) return x;
for(reg j=17;j>=0;--j){
if(fa[x][j]!=fa[y][j]) x=fa[x][j],y=fa[y][j];
}
return fa[x][0];
}
int be[2*N];
struct que{
int id,l,r,t;
int lca;
bool friend operator <(que a,que b){
if(be[a.l]==be[b.l]){
if(be[a.r]==be[b.r]){
if(be[a.r]&1) return a.t<b.t;
return a.t>b.t;
}
if(be[a.l]&1) return a.r<b.r;
return a.r>b.r;
}
return a.l<b.l;
}
}q[N];
int buc[N];
int vis[N];
ll now;
struct event{
int x,fr,to;
}h[N];
int num1,num2;
ll ans[N];
void upda(int id,int c){
if(c==1){
now+=v[id]*w[buc[id]+1];
}else{
now-=v[id]*w[buc[id]];
}
buc[id]+=c;
}
void chan(int x,int o){
int pos=a[x];
if(vis[pos]&1) upda(c[pos],-1);
else upda(c[pos],1);
vis[pos]+=o;
}
void add(int l,int r,int t){
if(vis[h[t].x]==1){
upda(c[h[t].x],-1);
c[h[t].x]=h[t].to;
upda(c[h[t].x],1);
}
c[h[t].x]=h[t].to;
}
void dele(int l,int r,int t){
if(vis[h[t].x]==1){
upda(c[h[t].x],-1);
c[h[t].x]=h[t].fr;
upda(c[h[t].x],1);
}
c[h[t].x]=h[t].fr;
}
void wrk(){
int l=0,r=0,t=0;
for(reg i=1;i<=num2;++i){
// cout<<" ii "<<i<<" : "<<q[i].id<<" : "<<q[i].l<<" "<<q[i].r<<" tt "<<q[i].t<<endl;
while(t<q[i].t) add(l,r,++t);
while(t>q[i].t) dele(l,r,t--);
while(r<q[i].r) chan(++r,1);
while(l>q[i].l) chan(--l,1);
while(r>q[i].r) chan(r--,-1);
while(l<q[i].l) chan(l++,-1);
if(q[i].lca){
ans[q[i].id]=now+v[c[q[i].lca]]*(w[buc[c[q[i].lca]]+1]);
}else{
ans[q[i].id]=now;
}
}
}
int main(){
rd(n);rd(m);rd(qs);
int blo=pow(qs,0.66666);
for(reg i=1;i<=m;++i) rd(v[i]);
for(reg i=1;i<=n;++i) rd(w[i]);
int x,y;
for(reg i=1;i<n;++i){
rd(x);rd(y);add(x,y);add(y,x);
}
for(reg i=1;i<=n;++i){
rd(c[i]);tmp[i]=c[i];
}
dfs(1,1);
for(reg j=1;j<=17;++j)
for(reg i=1;i<=n;++i){
fa[i][j]=fa[fa[i][j-1]][j-1];
}
for(reg i=1;i<=tot;++i){
be[i]=(i-1)/blo+1;
}
num1=0;
int op;//x,y;//,c;
for(reg i=1;i<=qs;++i){
rd(op);
if(op==0){
++num1;
rd(x);rd(y);
h[num1].x=x;h[num1].to=y;
h[num1].fr=tmp[x];
tmp[x]=y;
}else{
++num2;
rd(x);rd(y);
q[num2].id=num2;
q[num2].t=num1;
int anc=lca(x,y);
if(anc==x||anc==y){
if(in[x]>in[y]) swap(x,y);
q[num2].l=in[x],q[num2].r=in[y];
q[num2].lca=0;
}else{
q[num2].lca=anc;
if(out[x]>in[y]) swap(x,y);
q[num2].l=out[x],q[num2].r=in[y];
}
}
}
sort(q+1,q+num2+1);
wrk();
for(reg i=1;i<=num2;++i){
printf("%lld\n",ans[i]);
}
return 0;
}
}
signed main(){
Miracle::main();
return 0;
}
/*
Author: *Miracle*
Date: 2019/3/24 12:28:10
*/
可以离线的树上两点的查询也可以用莫队试试看
单点修改,时限又大的话,带修莫队也可以考虑的
进阶
1.卡常数:
直接变成序列加加减减的话,可能一个有很多点出现了两次,先加入再删除,不值得。
可以考虑直接找下一个路径,把相对的差做出来即可。
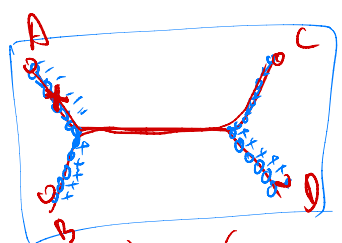
这样,排序还是按照序列排序,直接找路径显然常数只能更优
2.树上回滚莫队?
有些东西不能支持删除,只能栈序撤销
直接放到序列上再用回滚莫队还是要第二次加入的时候处理删除问题的。。。。。
直接在树上标关键点:
设深度是H的倍数,并且子树大小大于H的(防止被扫帚卡)设为关键点
关键点有n/H个
每个点距离最近的祖先关键点距离不超过2*H
每个询问放在第一个祖先的关键点上(x,y取较近的那一个)
每个关键点的询问:一路dfs,到了一个询问(x,y),这个时候dfs到了y,就直接找到较近的x,然后再从x退到关键点
复杂度:O(mH+(n/H)*n)
H=n/sqrt(m)时候最优
upda:2019.7.3
这个回滚莫队还要考虑一些特殊情况:
1.x,y询问挂的位置z应当使得x、y一个位于z子树,一个位于z的子树外。
2.如果不能达成1,那么这个询问一定距离<=2*H暴力即可。


