51Nod1220 约数之和

51Nod 1220 - 约数之和 

类比约数个数和那个题

如果知道：

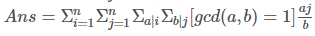
然后枚举约数，枚举gcd，用miu代替，大力反演一波

得到：

后面那个平方，其实是约数和的前缀和。线性筛预处理一部分，剩下的根号求解

前面的miu*i，杜教筛。

有意思的是：另一边推下来得到：（从右往左看）

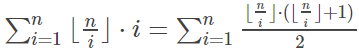
然后就凑成了那个平方。

 

Code；

记得sum是：n*(n+1)/2

 

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define int long long
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void ot(T x){x/10?ot(x/10):putchar(x%10+'0');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) printf("%lld ",a[i]);putchar('\n');}

namespace Miracle{
const int N=1e6+6;
const int mod=1e9+7;
int n;
int vis[N],miu[N];
ll sig[N];//miu  :  miu(i)*i and pre 
//sig : pre
int div[N];
int pri[N],tot;
int ad(int x,int y){
    return x+y>=mod?x+y-mod:x+y;
}
int sub(int x,int y){
    return x-y<0?x-y+mod:x-y;
}
void sieve(int n){
    miu[1]=1;sig[1]=1;
    div[1]=1;
    for(reg i=2;i<=n;++i){
        if(!vis[i]){
            pri[++tot]=i;
            miu[i]=-1;sig[i]=i+1;
            div[i]=i+1;
        }
        for(reg j=1;j<=tot;++j){
            if(i*pri[j]>n) break;
            vis[i*pri[j]]=1;
            if(i%pri[j]==0){
                miu[i*pri[j]]=0;
                sig[i*pri[j]]=sig[i]/div[i]*(div[i]*pri[j]+1);
                div[i*pri[j]]=div[i]*pri[j]+1;
                break;
            }
            miu[i*pri[j]]=-miu[i];
            sig[i*pri[j]]=sig[i]*sig[pri[j]];
            div[i*pri[j]]=pri[j]+1;
        }
    }
    for(reg i=1;i<=n;++i){
        miu[i]=ad((ll)i*ad(mod,miu[i])%mod,miu[i-1]);
        sig[i]%=mod;
        sig[i]=ad(sig[i],sig[i-1]);
    }
}
int Sum(int n){
    return (ll)n*(n+1)/2%mod;
}
int Sig(int n){
    if(n<N-5) return sig[n];
    int ret=0;
    for(reg i=1,x=0;i<=n;i=x+1){
        x=(n/(n/i));
        ret=ad(ret,(ll)sub(Sum(x),Sum(i-1))*(n/i)%mod);
    }
    return ret;
}
const int G=31630;
map<int,int>mp;
int sol(int n){
    if(n<=N-5) return miu[n];
    if(mp[n]) return mp[n];
    int ret=1;
    for(reg i=2,x=0;i<=n;i=x+1){
        x=(n/(n/i));
        ret=sub(ret,(ll)sub(Sum(x),Sum(i-1))*sol(n/i)%mod);
    }
    return mp[n]=ret;
}
int main(){
    rd(n);
    sieve(N-5);
    ll ans=0;
//    memset(p,-1,sizeof p);
    for(reg d=1,x=0;d<=n;d=x+1){
        x=n/(n/d);
        ll tmp=Sig(n/d);
        tmp=tmp*tmp%mod;
        ans=ad(ans,(ll)sub(sol(x),sol(d-1))*tmp%mod);
    }
    printf("%lld",ans);
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2019/3/8 14:52:26
*/