HDU 5608 - function

HDU 5608 - function 

套路题

图片来自：

 https://blog.csdn.net/V5ZSQ/article/details/52116285

 

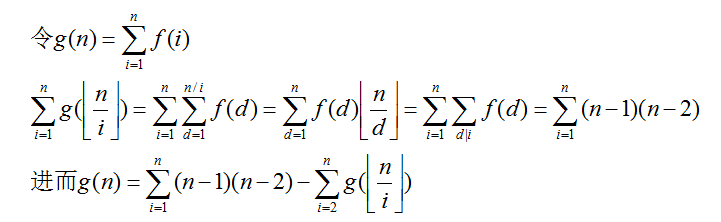
杜教筛思想，根号递归下去。

先搞出前缀和g(n)=∑f(i)

然后寻求递归。∑g(n/i)=常数

这一步要运用给出的f(i)的关系，干掉f

具体：

向枚举约数转化，不断交换求和，交换统计贡献的部分。通过数学意义变成枚举约数

 

然后类似杜教筛即可

f的前1000000项，调和级数枚举约数减去贡献

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void ot(T x){x/10?ot(x/10):putchar(x%10+'0');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) printf("%lld ",a[i]);putchar('\n');}

namespace Miracle{
const int mod=1e9+7;
const int M=1000000+6;
int t,n;
int f[M];
int qm(int x,int y){
    int ret=1;while(y){
        if(y&1) ret=(ll)ret*x%mod;x=(ll)x*x%mod;y>>=1;
    }return ret;
}
int ad(int x,int y){
    return x+y>=mod?x+y-mod:x+y;
}
void sieve(int n){
    for(reg i=1;i<=n;++i) f[i]=(ll)(i-1)*(i-2)%mod;
    for(reg i=1;i<=n;++i){
        for(reg j=i+i;j<=n;j+=i){
            f[j]=ad(f[j],mod-f[i]);
        }
    }
    for(reg i=1;i<=n;++i) f[i]=ad(f[i],f[i-1]);
}
map<int,int>mp;
int inv6;
int sol(int n){
    if(n<=M-5) return f[n];
    if(mp.find(n)!=mp.end()) return mp[n];
    ll ret=(ll)(n-1)*n%mod*(2*n-1)%mod*inv6%mod;
    ret=ad(ret,mod-(ll)n*(n-1)/2%mod);
    for(reg i=2,x=0;i<=n;i=x+1){
        x=(n/(n/i));
        ret=ad(ret,mod-(ll)(x-i+1)*sol(n/i)%mod);
    }
    return mp[n]=ret;
}
int main(){
    sieve(M-5);
    inv6=qm(6,mod-2);
    rd(t);
    while(t--){
        rd(n);printf("%d\n",sol(n));
    }
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2019/3/8 11:16:20
*/