[学习笔记]边分治
基于边的一种分治。统计过中心边的所有路径
可以类比点分治学习
构造：
每次找中心边（使得两侧的sz的最大值最小），然后递归下去
菊花图会卡成链，构造变成O(n^2)。
其实复杂度和度数相关
考虑转化成二叉树
三度化
法一：把所有儿子依次加一个点串起来
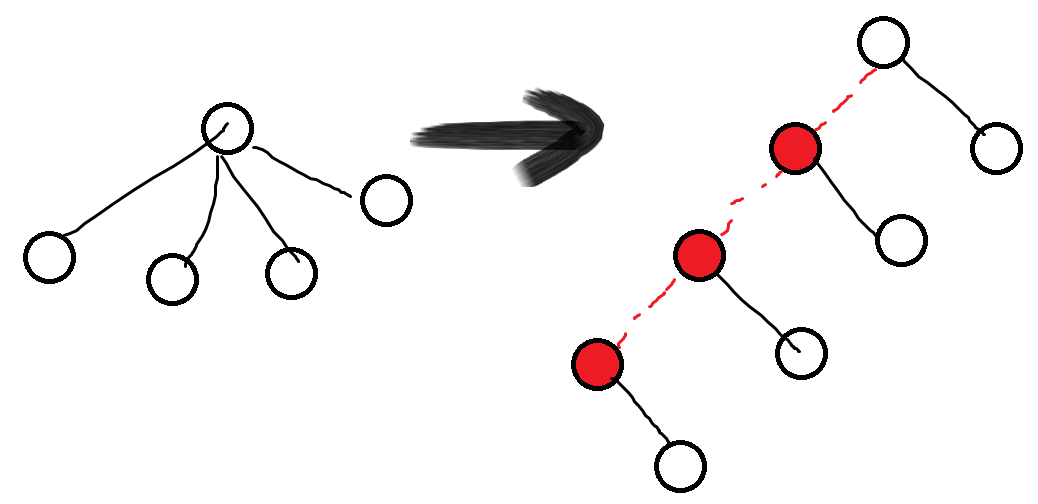
法二：
如果儿子多于2个，建立两个儿子虚点，把真正儿子奇偶分类给两个虚点
虚点放在n后面，最后会再处理到
所以其实边分治的分治树上的点有4*n个
本来n个点，rebuild变成2*n
而分治树除了叶子别的点都是边（类似于kruskal重构树），所以总共4*n个节点
性质：
二叉树
优劣：
优：1.二叉树儿子少，讨论减少了很多。复杂度基本严格logn
边分树儿子常数个（为2），每个点在这一层只有两种所属
边分树也是二叉树，为边分树合并提供条件
劣：2.虚点必须不影响答案
例题：
边分树使得每个点两个属性：[WC2018]通道
边分树是二叉树支持合并： [CTSC2018]暴力写挂——边分树合并
动态边分治
和点分治一样
分治树上只有了2个儿子，处理儿子的贡献就很好办了
关键还是避免虚点虚边的影响了
把虚点设置为黑点。也就可以边分治做了
