[学习笔记]凸优化/WQS二分/带权二分
从一个题带入:[八省联考2018]林克卡特树lct——WQS二分
比较详细的:
简单总结和补充:
条件
凸函数,限制
方法:
二分斜率,找切点横纵坐标,判断k的位置
找切点坐标:
集体-mid*x(证明还是凸函数:f(x+2)-f(x+1)<=f(x+1)-f(x))仍然成立)
每次选择物品有额外代价,
找此时高点就是原凸包切点
为了避免凸包上多点共线并且线的横坐标区域包含k,从而使得不会二分到k,
我们ans不记录符合条件切点的纵坐标,而是记录下来符合切点坐标(大于等于/小于等于)k的(最大/最小)斜率。(因题而异)
最后把斜率带进去求出纵坐标,然后向上平移ans*k即可
进阶:
k是一个区间[l,r]也可以做
法一:求出最高点选择的最大值最小值,根据斜率再调整
法二:求出l位置的切点斜率k1,r位置的切点斜率k2,如果k1,k2异号,k=0的切点就是最优位置,否则,绝对值更小的k的l或者r就是最优解位置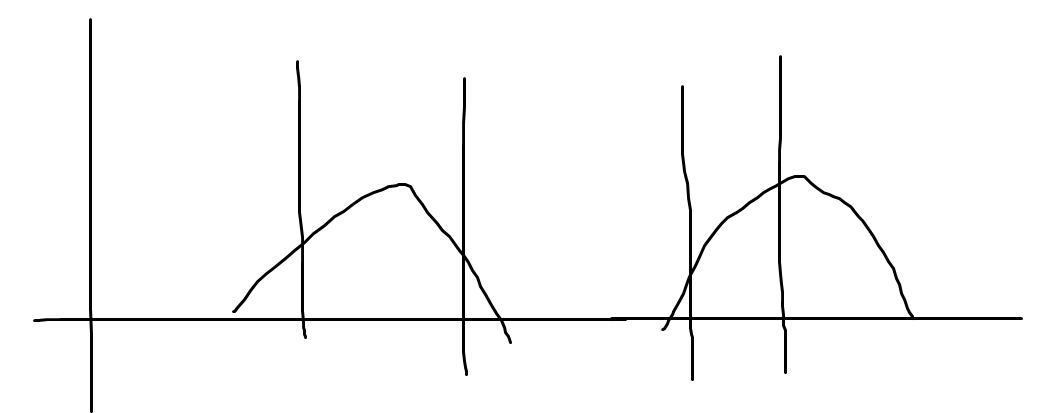
感悟
利用凸函数上二分,再转化为求“任意选择”全局最优解,使得摆脱了k的限制,使得DP维数降低,O(n^2)-O(nlogn)
upda:2021.7.17
这个题,和s的连边就是物品,要强制选K个。
一样的方法,二分mid。这个是下凸函数,所以减去mid以后,求最小生成树即可(得到最低点)
同样,为了避免横坐标为k的点在直线中间的问题,也是求直线最左端点和对应mid,最后再还原到k
注意impossible的判断!
1.连通
2.s至少度数为k
3.x=k在定义域内。
对于3这里要理解:
本质上,凸函数有定义域。这个定义域不用提前求,但是要在求出答案的mid之后,拓展出这个mid对应的最左最右端点,看有没有包含k即可。


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步