Winter And Snowmen

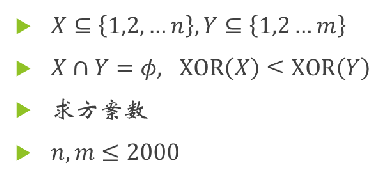
https://vjudge.net/problem/TopCoder-12891

暴力想法是：dp[i][s1][s2]前i个，第一个集合xor是s1，第二个集合xor是s2方案数O(n^3)

 

有xor

不妨按位考虑

枚举两个集合xor的LCP长度L

考虑从高到低前L位相同，第L+1位xor(X)=0,xor(Y)=1的方案数

剩下的低位就随便选择了

f[i][s][0/1][0/1]表示前i个数，前L位高位的xor和是s,第L+1位分别是0/1,0/1的方案数

每一个合法的方案都会被枚举到恰好一次。

复杂度：O(logn*n*(n/logn)=n^2)

代码：
（Topcoder还要class。。。）

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
    const int mod=1e9+7;
    const int N=2002;
    int n,m;
    int ans=0;
    int f[N][2049][2][2];
    int mo(int x,int y){
        return x+y>=mod?x+y-mod:x+y;
    }
class WinterAndSnowmen {
public:
    int getNumber(int n, int m) {
    
            int U=max(n,m);
            for(reg p=10;p>=0;--p){
                memset(f,0,sizeof f);
                f[0][0][0][0]=1;
                for(reg i=0;i<U;++i){//calc i+1
                    for(reg s=0;s<(1<<(11-p));++s){
                        for(reg l1=0;l1<=1;++l1){
                            for(reg l2=0;l2<=1;++l2){
                                int num=i+1;
                                f[i+1][s][l1][l2]=mo(f[i+1][s][l1][l2],f[i][s][l1][l2]);
                                if(i+1<=n)f[i+1][s^(num>>(p+1))][l1^((num>>p)&1)][l2]=mo(f[i+1][s^(num>>(p+1))][l1^((num>>p)&1)][l2],f[i][s][l1][l2]);
                                if(i+1<=m)f[i+1][s^(num>>(p+1))][l1][l2^((num>>p)&1)]=mo(f[i+1][s^(num>>(p+1))][l1][l2^((num>>p)&1)],f[i][s][l1][l2]);
                            }
                        }
                    }
                }
                ans=mo(ans,f[U][0][0][1]);
            }
            return ans;
    }
};